陕西省西安市2022-2023学年九年级下学期第一次质量监测数学试卷
试卷更新日期:2023-03-24 类型:月考试卷
一、单选题
-
1. 的倒数是( )A、3 B、-3 C、 D、2. 如图,将三角尺的直角顶点放在直尺的一边上, , , 则的度数等于( )
 A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知正比例函数中,随的增大而增大,则一次函数的图象所经过的象限是( )A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四5. 如图是的高, , , , 则的长为( ).
A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知正比例函数中,随的增大而增大,则一次函数的图象所经过的象限是( )A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四5. 如图是的高, , , , 则的长为( ).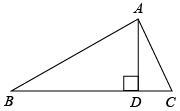 A、 B、 C、 D、6. 如图,在矩形中, , E是的中点,于点F,则的长是( )
A、 B、 C、 D、6. 如图,在矩形中, , E是的中点,于点F,则的长是( ) A、1 B、1.2 C、 D、27. 已知二次函数及一次函数 , 将二次函数在轴下方的图像沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象(如图所示),当直线与新图象有4个交点时,的取值范围是( )
A、1 B、1.2 C、 D、27. 已知二次函数及一次函数 , 将二次函数在轴下方的图像沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象(如图所示),当直线与新图象有4个交点时,的取值范围是( )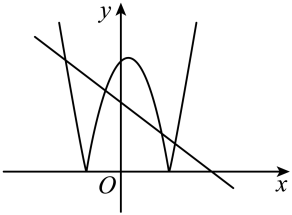 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 在实数 , , , 中有理数有个.9. 中国航天的脚步不只在月球,还迈向了400000000公里之外的火星,2021年,“天问一号”在火星留下了属于中国人的印记.数据400000000用科学记数法表示为.10. 若一个n边形的内角和是外角和的3倍,则n=.11. 如图,平行四边形的顶点在坐标原点上,在轴上,顶点在上,顶点在上,则平行四边形的面积是.
 12. 如图,在矩形ABCD中, , , 点E是矩形ABCD内部一动点,且 , 点P是边上一动点,连接 , 则的最小值为.
12. 如图,在矩形ABCD中, , , 点E是矩形ABCD内部一动点,且 , 点P是边上一动点,连接 , 则的最小值为.
三、解答题
-
13. 计算14. 先化简,再求值: , 其中.15. 解不等式 , 并把它的解集在数轴上表示出来.
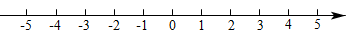 16. 解分式方程:17. 如图,荾形中,点 , 分别在边 , 上, , 求证:.
16. 解分式方程:17. 如图,荾形中,点 , 分别在边 , 上, , 求证:. 18. 如图方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,的顶点都在格点上,且三个顶点的坐标分别为 , , .
18. 如图方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,的顶点都在格点上,且三个顶点的坐标分别为 , , .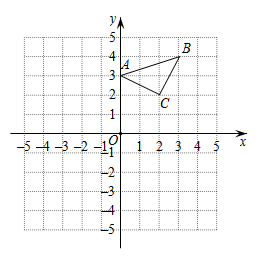 (1)、画出关于原点O的中心对称图形 , 并写出点B的对应点的坐标.(2)、画出将绕原点O逆时针方向旋转后的图形.19. 2022年10月12日16:01,“天宫课堂”第三课在中国空间站开讲,神舟十四号航天员陈冬、刘洋、蔡旭哲作为“太空教师”,分别为大家演示了:①微重力环境下毛细效应实验,②水球变“懒”实验,③太空趣味饮水,④旋转类演示实验“会调头的扳手”.杨老师组织同学观看四个实验后写感想.杨老师将四个实验的名称分别写在四张完全相同的卡片上,背面朝上,每位同学随机抽取一张,做好记录后放回,并向同伴分享对应实验的观看收获(1)、小明抽到写有“太空趣味饮水”卡片,并分享观后收获的概率为(2)、通过列表或对状图,求出小明和同桌小华刚好都抽到写有“会调头的扳手”卡片,并分享观后收获的概率.20. 如图,已知 , 请用尺规作图法,求作的一个内接正方形(保留作图痕迹,不写作法).
(1)、画出关于原点O的中心对称图形 , 并写出点B的对应点的坐标.(2)、画出将绕原点O逆时针方向旋转后的图形.19. 2022年10月12日16:01,“天宫课堂”第三课在中国空间站开讲,神舟十四号航天员陈冬、刘洋、蔡旭哲作为“太空教师”,分别为大家演示了:①微重力环境下毛细效应实验,②水球变“懒”实验,③太空趣味饮水,④旋转类演示实验“会调头的扳手”.杨老师组织同学观看四个实验后写感想.杨老师将四个实验的名称分别写在四张完全相同的卡片上,背面朝上,每位同学随机抽取一张,做好记录后放回,并向同伴分享对应实验的观看收获(1)、小明抽到写有“太空趣味饮水”卡片,并分享观后收获的概率为(2)、通过列表或对状图,求出小明和同桌小华刚好都抽到写有“会调头的扳手”卡片,并分享观后收获的概率.20. 如图,已知 , 请用尺规作图法,求作的一个内接正方形(保留作图痕迹,不写作法). 21. 下图是某种云梯车的示意图,云梯升起时,与底盘夹角为 , 液压杆与底盘夹角为.已知液压杆m,当 , 时,求的长.(参考数据: , , , ).
21. 下图是某种云梯车的示意图,云梯升起时,与底盘夹角为 , 液压杆与底盘夹角为.已知液压杆m,当 , 时,求的长.(参考数据: , , , ). 22. 我校为了解初三学生对于体育中考三大球项目中的排球技能掌握情况,在本校随机抽取了若干名初三学生进行测试,其中男生50名.将测试结果统计如下:
22. 我校为了解初三学生对于体育中考三大球项目中的排球技能掌握情况,在本校随机抽取了若干名初三学生进行测试,其中男生50名.将测试结果统计如下:40秒内垫球个数(x)
频数(男生)
2
10
9
10
频数(女生)
1
8
14
5
被抽取初三女生40秒垫球个数统计图

根据上述信息回答下列问题:
(1)、求得 , .(2)、被抽取初三女生40秒垫球个数的中位数所落在的范围是.(3)、若我校今年参加中考的考生有500人,其中男生有300人,女生有200人,请你估计在我校今年参加中考的考生中排球技能能取得满分的人数.(男生40秒垫球45个及以上为满分,女生40秒内垫球40个及以上为满分)23. 某玩具店购进2022年冬奥会吉祥物冰墩墩与冬残奥会吉祥物雪容融共120个,花去3350元,这两种吉祥物的进价、售价如表:
进价(元/个)
售价(元/个)
冰墩墩
30
45
雪容融
25
35
(1)、求冰墩墩、雪容融各购进了多少个?(2)、售卖中途由于冰墩墩受到广大游客的喜爱被一抢而空,商家又紧急购进了一批冰墩墩,最后和雪容融一起被卖完.若已知商家最后获取的利润不少于4050元,请问商家第二次至少购进了多少个冰墩墩?24. 如图,是半圆的直径,为半圆上的点(不与 , 重合),连接 , 点为的中点,过点作 , 交的延长线于点 , 连接 , 交于点.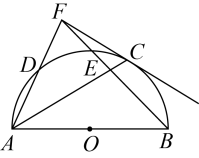 (1)、求证:是半圆的切线;(2)、若 , , 求半圆的半径及的长.25. 已知,如图,抛物线经过直线与坐标轴的两个交点 , , 此抛物线与轴的另一个交点为 , 抛物线的顶点为.
(1)、求证:是半圆的切线;(2)、若 , , 求半圆的半径及的长.25. 已知,如图,抛物线经过直线与坐标轴的两个交点 , , 此抛物线与轴的另一个交点为 , 抛物线的顶点为.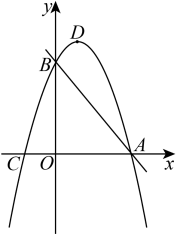 (1)、求此抛物线的解析式及顶点的坐标;(2)、在轴上是否存在点使为直角三角形?若存在,确定点的坐标:若不存在,请说明理由.26. 问题提出
(1)、求此抛物线的解析式及顶点的坐标;(2)、在轴上是否存在点使为直角三角形?若存在,确定点的坐标:若不存在,请说明理由.26. 问题提出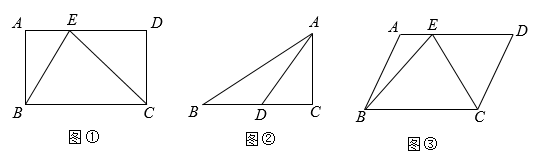 (1)、如图①,在矩形ABCD中,点E为AD边上一点,若S△BCE=4.则矩形ABCD的面积为_.(2)、问题探究
(1)、如图①,在矩形ABCD中,点E为AD边上一点,若S△BCE=4.则矩形ABCD的面积为_.(2)、问题探究
如图②.在△ABC中,∠BAC=60°,BC边上的中线AD=6,求△ABC面积的最大值.(3)、问题解决
为迎接十四运,园林设计部门准备在奥体广场用鲜花拼成一个平行四边形的花卉展览场地供市民观赏.如图③所示,在平行四边形ABCD中,点E为AD边上一点且DE=3AE,∠BEC=60°,AB=6米.为了种植更多的鲜花,要求四边形ABCD的面积尽可能大.请问四边形ABCD面积是否存在最大值?如果存在,请计算四边形ABCD面积的最大值;如果不存在,请说明理由.