浙江省2023年初中学业水平评价考试模拟预测数学试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
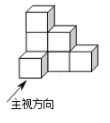
1. 在下列各数中,是无理数的是( )A、 B、 C、 D、2. 由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
 A、
A、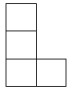 B、
B、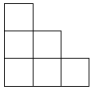 C、
C、 D、
D、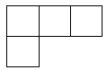 3. 绍兴市文化广电旅游局的统计表明,2019年春节黄金周7天,绍兴市共接待游客人次,同比增长 , 绍兴旅游实现“开门红”.其中数据用科学记数法可表示为( )A、 B、 C、 D、4. 一个不透明的箱子里装有1个白球,1个黄球和3个红球,这些球除颜色不同外其他都相同,则从箱子中随机摸出两个球,下列事件属于不可能事件的是( )A、摸出的球都是红球 B、摸出的球都是白球 C、摸出1个红球,1个白球 D、摸出1个红球,1个黄球5. 疫情期间,小明同学居家进行体育锻炼,下表是他今日5组引体向上的个数.在这5组数据中,众数和中位数分别是( )
3. 绍兴市文化广电旅游局的统计表明,2019年春节黄金周7天,绍兴市共接待游客人次,同比增长 , 绍兴旅游实现“开门红”.其中数据用科学记数法可表示为( )A、 B、 C、 D、4. 一个不透明的箱子里装有1个白球,1个黄球和3个红球,这些球除颜色不同外其他都相同,则从箱子中随机摸出两个球,下列事件属于不可能事件的是( )A、摸出的球都是红球 B、摸出的球都是白球 C、摸出1个红球,1个白球 D、摸出1个红球,1个黄球5. 疫情期间,小明同学居家进行体育锻炼,下表是他今日5组引体向上的个数.在这5组数据中,众数和中位数分别是( )第1组
第2组
第3组
第4组
第5组
14
13
14
12
11
A、13,14 B、13,13 C、14,13 D、14,146. 如图,在中,是边上的高,.点E为边的中点,连接.若 , 则高的长为( ) A、6 B、7 C、8 D、97. 已知点两点均在二次函数的图象上,则b的值为( )A、 B、2 C、 D、48. 一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集是( )
A、6 B、7 C、8 D、97. 已知点两点均在二次函数的图象上,则b的值为( )A、 B、2 C、 D、48. 一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集是( ) A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若FB=FE=2,FC=1,则AC的长是( )
A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若FB=FE=2,FC=1,则AC的长是( )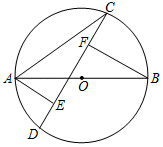 A、 B、 C、 D、10. 如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知: , 则直至两车都各自到达终点时,两车相遇的次数为( )
A、 B、 C、 D、10. 如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知: , 则直至两车都各自到达终点时,两车相遇的次数为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 因式分解: .
12. 在平面直角坐标系中,点A在第三象限,点B在第四象限,且点A、B关于y轴对称.若点B的坐标为 , 则点A的坐标为.(用字母表示)13. 如图,在平行四边形中, , 以点B为圆心,长为半径作弧,交直线与点E,连接 , 则的度数为. 14. 如图,等腰三角形和等腰三角形的顶点A、C都落在反比例函数的图象上.已知 , , 则的面积为.
14. 如图,等腰三角形和等腰三角形的顶点A、C都落在反比例函数的图象上.已知 , , 则的面积为. 15. 如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为.
15. 如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为.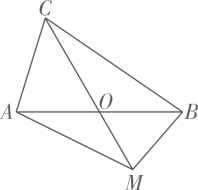 16. 如图,在中,对角线交于点O.点M是边的中点,连接 , 作.已知平分 , 平分 , 若 , 则的值为.
16. 如图,在中,对角线交于点O.点M是边的中点,连接 , 作.已知平分 , 平分 , 若 , 则的值为.
三、解答题
-
17. 计算:.18. 解方程组19. 某兴趣小组针对视力情况随机抽取本校部分学生进行调查,将调查结果进行统计分析,绘制成如下不完整的统计图表.
抽取的学生视力情况统计表
类别
调查结果
人数
A
正常
48
B
轻度近视
76
C
中度近视
60
D
重度近视
m
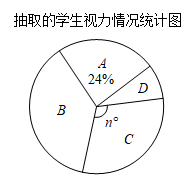
请根据图表信息解答下列问题:
(1)、填空:m= , n= ;(2)、该校共有学生1600人,请估算该校学生中“中度近视”的人数;(3)、某班有四名重度近视的学生甲、乙、丙、丁,从中随机选择两名学生参加学校组织的“爱眼护眼”座谈会,请用列表或画树状图的方法求同时选中甲和乙的概率.20. 如图,在矩形中, , 连结对角线.点M为线段上的一点,点N为线段上的一点,连结.回答下列问题: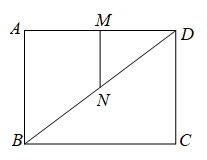 (1)、当点M为的中点且时,求的长.(2)、当且时,求的长.21. 如图,在半径为6的中,是直径.已知: , 点D是弧的中点,连接交与点F,作.回答下列问题:
(1)、当点M为的中点且时,求的长.(2)、当且时,求的长.21. 如图,在半径为6的中,是直径.已知: , 点D是弧的中点,连接交与点F,作.回答下列问题: (1)、求证:点C是弧的三等分点.(2)、求的长.22. 如图,正方形的边长为 , E,F分别是的中点,与分别交于点M,N. 请你回答下列问题:
(1)、求证:点C是弧的三等分点.(2)、求的长.22. 如图,正方形的边长为 , E,F分别是的中点,与分别交于点M,N. 请你回答下列问题: (1)、求证:.(2)、直接写出的长.(3)、求的面积.23.(1)、【阅读材料】如图①,四边形ABCD中, , 点E,F分别在上,若 , 求证:.
(1)、求证:.(2)、直接写出的长.(3)、求的面积.23.(1)、【阅读材料】如图①,四边形ABCD中, , 点E,F分别在上,若 , 求证:.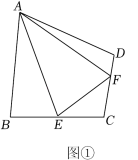 (2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)
(2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)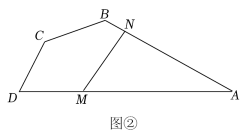 24. 如图,在平面直角坐标系中,点 , 以为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结 , 并延长至点D,使 , 过点D作x轴垂线,分别交x轴、直线于点E、F,点E为垂足,连结.
24. 如图,在平面直角坐标系中,点 , 以为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结 , 并延长至点D,使 , 过点D作x轴垂线,分别交x轴、直线于点E、F,点E为垂足,连结. (1)、当时,求弧的长度;(2)、当时,求线段的长;(3)、在点B运动过程中,是否存在以点E、C、F为顶点的三角形与相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
(1)、当时,求弧的长度;(2)、当时,求线段的长;(3)、在点B运动过程中,是否存在以点E、C、F为顶点的三角形与相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.