新疆乌鲁木齐市2023年中考数学一模试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 实数﹣2023的绝对值是( )A、2023 B、﹣2023 C、 D、2. 下列命题中,假命题是( )A、对顶角相等 B、同一平面内,过一点有且只有一条直线与已知直线垂直 C、同一平面内,过直线外一点有且只有一条直线与这条直线平行 D、如果a>c,b>c,那么a>b3. 如果将抛物线向上平移1个单位,那么所得新抛物线的表达式是( )A、 B、 C、 D、4. 如图,小颖按下面方法用尺规作角平分线:在已知的的两边上,分别截取 , 使.再分别以点C,D为圆心、大于的长为半径作弧,两弧在内交于点P,作射线 , 则射线就是的平分线.其作图原理是: , 这样就有 , 那么判定这两个三角形全等的依据是( )
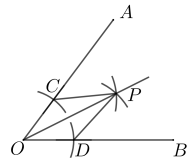 A、 B、 C、 D、5. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( )
A、 B、 C、 D、5. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( ) A、相离 B、相切 C、相交 D、不能确定6. 已知在中, , , 那么以边长的倍为半径的圆A与以为直径的圆的位置关系是( )A、外切 B、相交 C、内切 D、内含7. 如果将抛物线 向上平移 个单位,那么平移后抛物线的顶点坐标是( )A、 B、 C、 D、8. 在中, , 以点A为圆心,半径为8的圆记作圆A,那么下列说法正确的是( )A、点C在圆A内,点B在圆A外 B、点C在圆A上,点B在圆A外 C、点C、B都在圆A内 D、点C、B都在圆A外9. 将抛物线向右平移1个单位,再向上平移2个单位后,所得新抛物线和原抛物线相比,不变的是( )A、对称轴 B、开口方向 C、和y轴的交点 D、顶点.10. 如图,已知点D、E、F、G、H、I分别在的三边上,如果六边形是正六边形,下列结论中不正确的是( )
A、相离 B、相切 C、相交 D、不能确定6. 已知在中, , , 那么以边长的倍为半径的圆A与以为直径的圆的位置关系是( )A、外切 B、相交 C、内切 D、内含7. 如果将抛物线 向上平移 个单位,那么平移后抛物线的顶点坐标是( )A、 B、 C、 D、8. 在中, , 以点A为圆心,半径为8的圆记作圆A,那么下列说法正确的是( )A、点C在圆A内,点B在圆A外 B、点C在圆A上,点B在圆A外 C、点C、B都在圆A内 D、点C、B都在圆A外9. 将抛物线向右平移1个单位,再向上平移2个单位后,所得新抛物线和原抛物线相比,不变的是( )A、对称轴 B、开口方向 C、和y轴的交点 D、顶点.10. 如图,已知点D、E、F、G、H、I分别在的三边上,如果六边形是正六边形,下列结论中不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
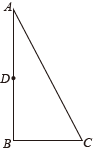
11. 抛物线y=﹣x2+2x﹣7与y轴的交点坐标为 .12. 如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上, , 则 .
 13. 如图,中, , , . 四边形是正方形,点D是直线BC上一点,且 . P是线段上一点,且 . 过点P作直线l于BC平行,分别交AB,AD于点G,H,则的长是 .
13. 如图,中, , , . 四边形是正方形,点D是直线BC上一点,且 . P是线段上一点,且 . 过点P作直线l于BC平行,分别交AB,AD于点G,H,则的长是 . 14. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 , 以点A为圆心,3为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与交于点K,连结HG、CH.给出下列四个结论.(1)H是FK的中点;(2);(3);(4) , 其中正确的结论有(填写所有正确结论的序号).
14. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 , 以点A为圆心,3为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与交于点K,连结HG、CH.给出下列四个结论.(1)H是FK的中点;(2);(3);(4) , 其中正确的结论有(填写所有正确结论的序号).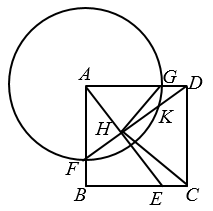 15. 正方形ABCD中,AB=2 , 点M是BC中点,点P是正方形内一点,连接PC,PM,当点P移动时,始终保持∠MPC=45°,连接BP,点E,F分别是AB,BP中点,求3BP+2EF的最小值为.
15. 正方形ABCD中,AB=2 , 点M是BC中点,点P是正方形内一点,连接PC,PM,当点P移动时,始终保持∠MPC=45°,连接BP,点E,F分别是AB,BP中点,求3BP+2EF的最小值为.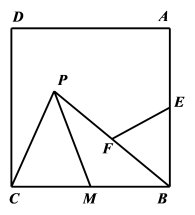
三、解答题
-
16. 计算:(1)、;(2)、;(3)、.17. 如图,直线l与a、b相交于点A、B,且 .
 (1)、尺规作图:过点B作的角平分线交直线a于点D(保留作图痕迹,标注有关字母,不用写作法和证明);(2)、若 , 求的度数;(3)、P为直线l上任意一点,若点D到直线b的距离为 , 则DP的最小值为cm.18. 如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.
(1)、尺规作图:过点B作的角平分线交直线a于点D(保留作图痕迹,标注有关字母,不用写作法和证明);(2)、若 , 求的度数;(3)、P为直线l上任意一点,若点D到直线b的距离为 , 则DP的最小值为cm.18. 如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.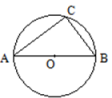 (1)、尺规作图:过点O作AC的垂线,交劣弧于点D,连接CD(保留作图痕迹,不写作法);(2)、在(1)所作的图形中,求点O到AC的距离及sin∠ACD 的值.19. 动手操作题: 如图,三角形ABC, 按要求画图并填空,通过测量解决下面的问题:
(1)、尺规作图:过点O作AC的垂线,交劣弧于点D,连接CD(保留作图痕迹,不写作法);(2)、在(1)所作的图形中,求点O到AC的距离及sin∠ACD 的值.19. 动手操作题: 如图,三角形ABC, 按要求画图并填空,通过测量解决下面的问题: (1)、作∠ABC的平分线,交AC于点D;(2)、过点D作BC的平行线,交AB于点E;(3)、写出一对相等的角(角平分线平分的两个角相等除外);(4)、写出一对相等的线段 .20. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下
(1)、作∠ABC的平分线,交AC于点D;(2)、过点D作BC的平行线,交AB于点E;(3)、写出一对相等的角(角平分线平分的两个角相等除外);(4)、写出一对相等的线段 .20. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单长度后得到的点Q' 也在G上时,求G在≤≤的图象的最高点的坐标.
21. 如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.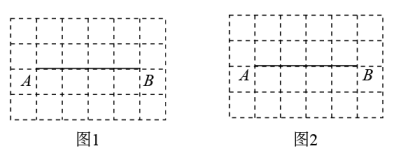 (1)、在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.22. 请仅用无刻度的直尺在网格中完成下列作图,保留作图痕迹,不写作法.
(1)、在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.22. 请仅用无刻度的直尺在网格中完成下列作图,保留作图痕迹,不写作法. (1)、图是由边长为的小等边三角形构成的网格,为格点三角形.在图中,画出中边上的中线;(2)、如图 , 四边形中, , , 画出边的垂直平分线.23. 下面是小李设计的“利用直角和线段作矩形”的尺规作图过程.
(1)、图是由边长为的小等边三角形构成的网格,为格点三角形.在图中,画出中边上的中线;(2)、如图 , 四边形中, , , 画出边的垂直平分线.23. 下面是小李设计的“利用直角和线段作矩形”的尺规作图过程.
已知:如图 , 线段 , , 及 .
求作:矩形 , 使 , .
作法:如图 ,
①在射线 , 上分别截取 , ;
②以为圆心,长为半径作弧,再以为圆心,长为半径作弧,两弧在内部交于点;
③连接 , .
四边形就是所求作的矩形.
根据小李设计的尺规作图过程,解答下列问题:
(1)、使用直尺和圆规,依作法补全图(保留作图痕迹);(2)、完成下面的证明.证明: , ▲ ,
四边形是平行四边形( )(填推理的依据).
,
四边形是矩形( )(填推理的依据).