四川省绵阳市游仙区2023年九年级学情监测数学试题(游仙二诊)
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 点关于坐标原点的中心对称点为( )A、 B、 C、 D、2. 下测图形中,中心对称图形的个数是( )
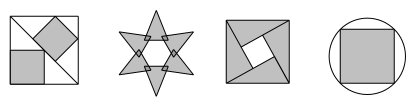 A、1个 B、2个 C、3个 D、4个3. 2022年3月23日下午,“天宫课堂”第二课在中国空间站正式开讲并直播,神舟十三号乘组航天员翟志刚、王亚平、叶光富进行授课.央视新闻抖音号进行全程直播,共吸引315万网友观看,其中315万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 关于反比例函数的图象——双曲线,下列说法不正确的是( )A、过双曲线上任意一点M作y轴的垂线,垂足为点N,则的面积为6. B、此双曲线分布在第二、四象限,y随x的增大而增大. C、双曲线关于直线成轴对称 D、此双曲线上的点到原点的最短距离为6. 2022年的绵阳体育中考的总分为80分,也是我市首次采用必考项目智能化测试设备.在此次体育中考中,某校6名学生的体育成绩统计如图所示,则对这组数据的说法中错误的是( )
A、1个 B、2个 C、3个 D、4个3. 2022年3月23日下午,“天宫课堂”第二课在中国空间站正式开讲并直播,神舟十三号乘组航天员翟志刚、王亚平、叶光富进行授课.央视新闻抖音号进行全程直播,共吸引315万网友观看,其中315万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 关于反比例函数的图象——双曲线,下列说法不正确的是( )A、过双曲线上任意一点M作y轴的垂线,垂足为点N,则的面积为6. B、此双曲线分布在第二、四象限,y随x的增大而增大. C、双曲线关于直线成轴对称 D、此双曲线上的点到原点的最短距离为6. 2022年的绵阳体育中考的总分为80分,也是我市首次采用必考项目智能化测试设备.在此次体育中考中,某校6名学生的体育成绩统计如图所示,则对这组数据的说法中错误的是( )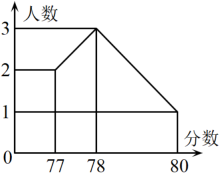 A、方差为1 B、中位数为78 C、众数为78 D、极差为27. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、且 C、 D、且8. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,则它的俯视图是( )
A、方差为1 B、中位数为78 C、众数为78 D、极差为27. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、且 C、 D、且8. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,则它的俯视图是( )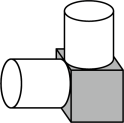 A、
A、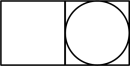 B、
B、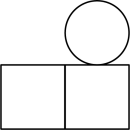 C、
C、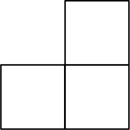 D、
D、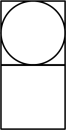 9. 把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
9. 把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )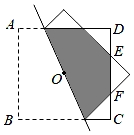 A、1 B、2 C、 D、210. 年月日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务收得圆满成功,中国航天,又站在了一个新的起点.如图年月日,神舟十三号载人飞船从地面处成功发射,当飞船到达点时,地面处的雷达站测得米,仰角为 , 秒后,飞船直线上升到达点处,此时地面处的雷达站测得处的仰角为.点 , , 在同一直线上,已知 , 两处相距米,则飞船从到处的平均速度为( )米秒.(结果精确到米;参考数据: , )
A、1 B、2 C、 D、210. 年月日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务收得圆满成功,中国航天,又站在了一个新的起点.如图年月日,神舟十三号载人飞船从地面处成功发射,当飞船到达点时,地面处的雷达站测得米,仰角为 , 秒后,飞船直线上升到达点处,此时地面处的雷达站测得处的仰角为.点 , , 在同一直线上,已知 , 两处相距米,则飞船从到处的平均速度为( )米秒.(结果精确到米;参考数据: , ) A、336 B、335 C、334 D、33311. 不等式组的所有整数解的和为9,则整数的值有( )A、1个 B、2个 C、3个 D、4个12. 如图,在中, , , , 点P是延长线上一动点,边与点M,边与点N,连接 , 则的最小值为( )
A、336 B、335 C、334 D、33311. 不等式组的所有整数解的和为9,则整数的值有( )A、1个 B、2个 C、3个 D、4个12. 如图,在中, , , , 点P是延长线上一动点,边与点M,边与点N,连接 , 则的最小值为( )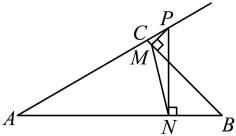 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
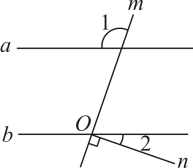
13. 因式分解:﹣3am2+12an2= .14. 如图,直线 , 直线 , 垂足О在直线上.若 , 则的度数为.
 15. 把一些书分给几名同学,如果每人分3本,那么余8本,如果前面的每名同学分5本,那么最后一人分不到3本,那么这些书共有本.16. 如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是.
15. 把一些书分给几名同学,如果每人分3本,那么余8本,如果前面的每名同学分5本,那么最后一人分不到3本,那么这些书共有本.16. 如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是. 17. 如图, , 反比例函数的图象过点B,若点A的坐标为 , , 则.
17. 如图, , 反比例函数的图象过点B,若点A的坐标为 , , 则.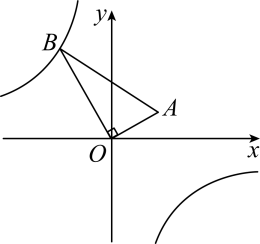 18. 中, , 把绕点A逆时针旋转度 , 得到 , 点B,C的对应点分别为点D,E,连接EC并延长交BD于点P.若 , 则的值为.
18. 中, , 把绕点A逆时针旋转度 , 得到 , 点B,C的对应点分别为点D,E,连接EC并延长交BD于点P.若 , 则的值为.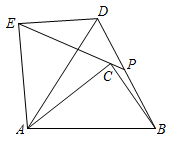
三、解答题
-
19.(1)、计算:;(2)、化简求值: , 其中 , .20. 最近,胜利中学掀起了志愿服务的热潮,政教处也号召各班学生积极参与,为了解某年级学生一周服务情况,从这个年级中随机抽取若干名学生,分别对他们一周的志愿服务时长(单位:分钟)进行收集、整理、分析,绘制出了这些学生一周的志愿服务时长的扇形统计图如图(数据分成6组):A. , B. , C. , D. , E. , F.;其中这些学生一周志愿服务时长在C. , 这一组的是:78 60 66 72 75 62 78 73 69 75 60 73 64 75.
根据以上信息,回答下列问题:
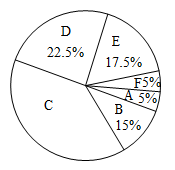 (1)、被随机抽取的学生人数为 , 扇形统计图中“C组”所对应的圆心角的度数为.(2)、分别求出“C组”志愿服务时长的平均数、中位数、众数;(3)、小红和小丹两位同学都参加了富乐街道的志愿者服务项目,该街道志愿者服务工作一共设置了三个岗位,请用列表或画树状图的方法,求小红、小丹恰好被分配到同一岗位进行志愿者服务的概率.21. 2022年3月1日,新冠疫情卷土重来,疫情发生后,市政府高度重视,并第一时间启动应急预案,迅速做好疫情防控工作,由于疫情原因,市急需大量物资.某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为3万元/吨,乙物资单价为2万元/吨,采购两种物资共花费1380万元.(1)、甲、乙两种物资各采购了多少吨?(2)、现在计划安排A,B两种不同规格的卡车共50辆来运输这批物资,A种卡车每辆需付运输费1500元,B种卡车每辆需付运输费1300元.甲物资7吨和乙物资3吨可装满一辆A型卡车;甲物资5吨和乙物资7吨可装满一辆B型卡车.按此要求安排A,B两型卡车的数量,请问有几种运输方案﹖哪种运输方案的运输费最少,并求此时的运输费.22. 如图,在平面直角坐标系中,一次函数的图象分别交x轴,y轴正半轴于点A,B,内切于 , 反比例函数的图象经过点P,交直线于点C,D(C在点D的左侧).
(1)、被随机抽取的学生人数为 , 扇形统计图中“C组”所对应的圆心角的度数为.(2)、分别求出“C组”志愿服务时长的平均数、中位数、众数;(3)、小红和小丹两位同学都参加了富乐街道的志愿者服务项目,该街道志愿者服务工作一共设置了三个岗位,请用列表或画树状图的方法,求小红、小丹恰好被分配到同一岗位进行志愿者服务的概率.21. 2022年3月1日,新冠疫情卷土重来,疫情发生后,市政府高度重视,并第一时间启动应急预案,迅速做好疫情防控工作,由于疫情原因,市急需大量物资.某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为3万元/吨,乙物资单价为2万元/吨,采购两种物资共花费1380万元.(1)、甲、乙两种物资各采购了多少吨?(2)、现在计划安排A,B两种不同规格的卡车共50辆来运输这批物资,A种卡车每辆需付运输费1500元,B种卡车每辆需付运输费1300元.甲物资7吨和乙物资3吨可装满一辆A型卡车;甲物资5吨和乙物资7吨可装满一辆B型卡车.按此要求安排A,B两型卡车的数量,请问有几种运输方案﹖哪种运输方案的运输费最少,并求此时的运输费.22. 如图,在平面直角坐标系中,一次函数的图象分别交x轴,y轴正半轴于点A,B,内切于 , 反比例函数的图象经过点P,交直线于点C,D(C在点D的左侧).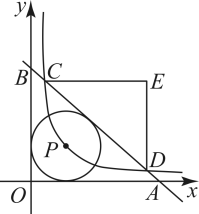 (1)、求反比例函数的解析式;(2)、过点C,D分别作x轴,y轴的平行线交于点E,求的面积.23. 如图,点E是的内心,的延长线和的外接圆相交于点D.
(1)、求反比例函数的解析式;(2)、过点C,D分别作x轴,y轴的平行线交于点E,求的面积.23. 如图,点E是的内心,的延长线和的外接圆相交于点D.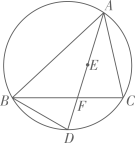 (1)、求证:;(2)、已知 , , 求该圆的半径的长度;(3)、在(2)的条件下,若 , 求的值.24. 如图,矩形中, , 是边上的一点, , 是边的中点,动点从点出发,沿边以的速度向终点运动,过点作于点 , 连接 , 设动点的运动时间是.
(1)、求证:;(2)、已知 , , 求该圆的半径的长度;(3)、在(2)的条件下,若 , 求的值.24. 如图,矩形中, , 是边上的一点, , 是边的中点,动点从点出发,沿边以的速度向终点运动,过点作于点 , 连接 , 设动点的运动时间是.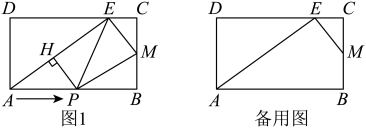 (1)、求为何值时,;(2)、设的面积为 , 写出与之间的函数关系式;(3)、当平分四边形的面积时,求的值.25. 抛物线与x轴分别交于 , 两点(点在点的左侧),与轴交于点 , 抛物线对称轴为 , 点是第一象限抛物线上动点,连接 , .
(1)、求为何值时,;(2)、设的面积为 , 写出与之间的函数关系式;(3)、当平分四边形的面积时,求的值.25. 抛物线与x轴分别交于 , 两点(点在点的左侧),与轴交于点 , 抛物线对称轴为 , 点是第一象限抛物线上动点,连接 , .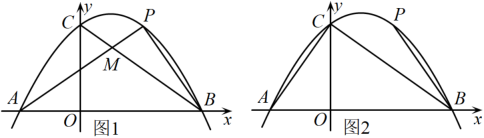 (1)、求抛物线和直线的解析式;(2)、如图1,连接 , 交于点 , 设的面积为 , 的面积为 , 求的最小值及此时点的坐标;(3)、如图2,设 , 在直线上方的抛物线上是否存在点 , 使得恰好等于 , 若存在,求出点的横坐标;若不存在,请说明理由.
(1)、求抛物线和直线的解析式;(2)、如图1,连接 , 交于点 , 设的面积为 , 的面积为 , 求的最小值及此时点的坐标;(3)、如图2,设 , 在直线上方的抛物线上是否存在点 , 使得恰好等于 , 若存在,求出点的横坐标;若不存在,请说明理由.