四川省成都市2023年中考模拟数学试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 下列是正方体展开图的是( )A、
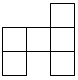 B、
B、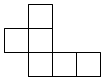 C、
C、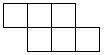 D、
D、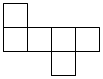 2. 一家商店将某种服装按成本提高标价,又以折优惠卖出,结果每件服装仍可获利元,则这种服装每件的成本价是( )A、元 B、元 C、元 D、元3. 中国华为麒麟9000处理器是采用5纳米制程工艺的手机芯片,在它的尺寸上塞进了153亿个晶体管,是世界上最先进的具有人工智能的手机处理,153亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示,在中, , 分别是 , 边上的高,并且 , 交于点 , 若 , 则等于( )
2. 一家商店将某种服装按成本提高标价,又以折优惠卖出,结果每件服装仍可获利元,则这种服装每件的成本价是( )A、元 B、元 C、元 D、元3. 中国华为麒麟9000处理器是采用5纳米制程工艺的手机芯片,在它的尺寸上塞进了153亿个晶体管,是世界上最先进的具有人工智能的手机处理,153亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示,在中, , 分别是 , 边上的高,并且 , 交于点 , 若 , 则等于( )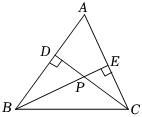 A、 B、 C、 D、5. 如图,的一条直角边在轴上,双曲线与的斜边相交于点C,与另一直角边相交于点.若 , 则与的面积比为( )
A、 B、 C、 D、5. 如图,的一条直角边在轴上,双曲线与的斜边相交于点C,与另一直角边相交于点.若 , 则与的面积比为( ) A、 B、 C、 D、6. 如图,在菱形中, , 点E,F分别是边上任意点(不与端点重合),且 , 连接相交于点G,连接与相交于点H,下列结论:①;②的大小为定值;③与一定不垂直;④若 , 则 , 其中正确的结论有( )
A、 B、 C、 D、6. 如图,在菱形中, , 点E,F分别是边上任意点(不与端点重合),且 , 连接相交于点G,连接与相交于点H,下列结论:①;②的大小为定值;③与一定不垂直;④若 , 则 , 其中正确的结论有( ) A、①② B、①②④ C、③④ D、①③④7. 如图,多边形是的内接正n边形,已知的半径为r,的度数为 , 点O到的距离为d,的面积为S.下面三个推断中.
A、①② B、①②④ C、③④ D、①③④7. 如图,多边形是的内接正n边形,已知的半径为r,的度数为 , 点O到的距离为d,的面积为S.下面三个推断中.
①当n变化时,随n的变化而变化,与n满足的函数关系是反比例函数关系;②若为定值,当r变化时,d随r的变化而变化,d与r满足的函数关系是正比例函数关系;③若n为定值,当r变化时,S随r的变化而变化,S与r满足的函数关系是二次函数关系.其中正确的是( )
A、①② B、①③ C、②③ D、①②③8. 如图是抛物线的一部分,其顶点为M,与y轴交于点 , 与x轴的一个交点为A,连接 , 给出以下四个结论:①;②抛物线经过点;③;④当时,.其中错误的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 定义为不大于x的最大整数,如 , , , 则满足 , 则的最大整数为.10. 如图,长方体中 , P为中点,在P处有一滴蜂蜜,一只蚂蚁从点A出发,沿长方体表面到点P处吃蜂蜜,那么它爬行的最短路程是.
 11. 如图,平面直角坐标系中,将含的三角尺的直角顶点落在第二象限.其斜边两端点、分别落轴、轴上,且 , 点与点的距离的最大值.
11. 如图,平面直角坐标系中,将含的三角尺的直角顶点落在第二象限.其斜边两端点、分别落轴、轴上,且 , 点与点的距离的最大值.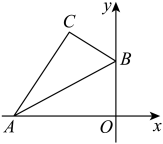 12. 如图,大楼高 , 远处有一塔 , 某人在楼底A处测得塔顶的仰角为 , 爬到楼顶D测得塔顶的仰角为 , 则塔高为m.
12. 如图,大楼高 , 远处有一塔 , 某人在楼底A处测得塔顶的仰角为 , 爬到楼顶D测得塔顶的仰角为 , 则塔高为m. 13. 如图,在矩形中, , , B为中点,连接.动点M从点O出发沿边向点A运动,动点N从点A出发沿边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接 , , , 设运动时间为秒.则时,为直角三角形.
13. 如图,在矩形中, , , B为中点,连接.动点M从点O出发沿边向点A运动,动点N从点A出发沿边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接 , , , 设运动时间为秒.则时,为直角三角形.
三、解答题
-
14.(1)、因式分解:(2)、已知 , , 求的值.15. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动自行车需要佩戴头盔.某日我市交警部门在某十字路口共拦截了50名不带头盔的摩托车、电动自行车骑行者,根据年龄段和性别得到如下表的统计信息:
年龄(岁)
人数
男性占比
4
25
8
3
请根据表中信息回答下列问题:
(1)、统计表中的值为;(2)、若按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“”部分所对应扇形的圆心角的度数为多少?(3)、若从年龄在“”的4人中,随机抽取2人参加交通安全知识学习,求恰好抽到2名男性的概率.16. 燕子洞是大自然赋予人类的神奇奥妙的天然大溶洞,只有真正走进燕子洞的人,才会领略到燕子洞雄奇壮美的自然景观,为大自然之神工妙笔所叹服,洞口垂直高度比世界吉尼斯纪录的马来西亚沙捞越洞高度还要高大,被称为“天下第一高大洞穴”.如图,小红到此地游玩,对燕子洞的高度颇感兴趣,于是用自己带来的无人机测量数据,再用自己以前学习过的三角函数知识来推算高度,已知无人机A与洞口水平距离是 , 从无人机A看燕子洞顶部B仰角为 , 看山洞底部C俯角为 , 小红看向无人机A的仰角为 , (参考数值:)
请回答以下问题:
(1)、请求出燕子洞的高度(结果精确到个位).(2)、若小红身高 , 此刻正站在一块高的岩石上操控无人机,请你求出小红与燕子洞洞口的水平距离(结果精确到个位).17. 如图,为的内接三角形, , 垂足为D,直径平分 , 交于点F,连结. (1)、求证:;(2)、若 , 求的长;(3)、若点G为的中点,连结 , 若点O在上,求的值.18. 定义:如图1,点P为平分线上一点,的两边分别与射线交于M,N两点,若绕点P旋转时始终满足 , 则称是的“梦之角”.
(1)、求证:;(2)、若 , 求的长;(3)、若点G为的中点,连结 , 若点O在上,求的值.18. 定义:如图1,点P为平分线上一点,的两边分别与射线交于M,N两点,若绕点P旋转时始终满足 , 则称是的“梦之角”.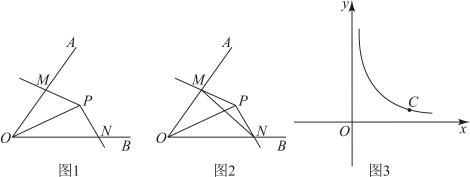 (1)、如图1,已知 , 点P为平分线上一点,的两边分别与射线交于M,N两点,且.求证:是的“梦之角”;(2)、如图2,已知 , , 若是的“梦之角”,连接 , 用含的式子分别表示的度数和的面积;(3)、如图3,C是函数图象上的一个动点,过点C的直线分别交x轴和y轴于点A,B两点,且满足 , 的“梦之角”为 , 请直接写出的长及相应点P的坐标.
(1)、如图1,已知 , 点P为平分线上一点,的两边分别与射线交于M,N两点,且.求证:是的“梦之角”;(2)、如图2,已知 , , 若是的“梦之角”,连接 , 用含的式子分别表示的度数和的面积;(3)、如图3,C是函数图象上的一个动点,过点C的直线分别交x轴和y轴于点A,B两点,且满足 , 的“梦之角”为 , 请直接写出的长及相应点P的坐标.四、填空题
-
19. 已知a,b,c为三个非负实数,且满足 , 若 , 则W的最大值为.20. 2021年11月2日,重庆市九龙坡区、长寿区分别新增1例新冠本土确诊.当疫情出现后,各级政府及有关部门高度重视,坚决阻断疫情传播.开州区赵家工业园区一家民营公司为了防疫需要,引进一条口罩生产线生产口罩,该产品有三种型号,通过市场调研后,按三种型号受消费者喜爱的程度分别对A型、B型、C型产品在成本的基础上分别加价20%,30%,45%出售(三种型号的成本相同).经过一个月的经营后,发现C型产品的销量占总销量的 , 且三种型号的总利润率为35%.第二个月,公司决定对A型产品进行升级,升级后A型产品的成本提高了25%,销量提高了20%;B型、C型产品的销量和成本均不变,且三种产品在第二个月成本基础上分别加价20%,30%,50%出售,则第二个月的总利润率为.21. 如图,已知中, , , 将绕A点逆时针旋转得到 , 以下结论:① , ② , ③ , ④ , 其中正确结论的序号是.
 22. 如图,“爱心”图案是由函数的部分图像与其关于直线的对称图形组成.点A是直线上方“爱心”图案上的任意一点,点B是其对称点.若 , 则点A的坐标是.
22. 如图,“爱心”图案是由函数的部分图像与其关于直线的对称图形组成.点A是直线上方“爱心”图案上的任意一点,点B是其对称点.若 , 则点A的坐标是.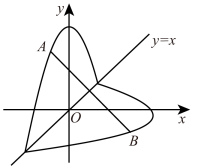 23. 已知:如图,中, , 圆C半径为6,P为斜边上的一个动点,分别与圆C相切于M、N,连接交于点Q,则的最小值为.
23. 已知:如图,中, , 圆C半径为6,P为斜边上的一个动点,分别与圆C相切于M、N,连接交于点Q,则的最小值为.
五、解答题
-
24. 近年来我国国内幼儿教育机器人发展趋势迅猛,市场上出现了满足各类要求的幼教机器人产品.“双十一”当天,某品牌幼教机器人专卖店抓住机遇,对最畅销的A款幼教机器人进行促销,一台A款幼教机器人的成本价为850元,标价为1300元.(1)、一台A款幼教机器人的价格最多降价多少元,才能使利润率不低于30%;(2)、该专卖店以前每周共售出A款幼教机器人100个,“双十一”狂购夜中每台A款幼教机器人在标价的基础上降价2m元,结果这天晚上卖出的A款幼教机器人的数量比原来一周卖出的A款幼教机器人的数量增加了m%,同时这天晚上的利润比原来一周的利润增加了m%,求m的值.25. 已知抛物线(是常数)与x轴交于A,B两点,A在B的左侧.(1)、若抛物线的对称轴为直线 , 求抛物线的解析式;(2)、在(1)的条件下, , 是抛物线上的两点,点P是线段CD下方抛物线上的一动点,连接PC,PD,求的面积最大值;(3)、已知代数式 , 记抛物线位于轴下方的图象为 , 抛物线位于x轴上方的图象为 , 将沿轴翻折得图象 , 与组合成的新图象记为 , 当直线与图象T有两个交点时,结合图象求M的取值范围.26. 如图.已知为等腰直角三角形, , D、E分别为上的两点, , 连接 , 将绕点E逆时针旋转得 , 连接与交于点M.
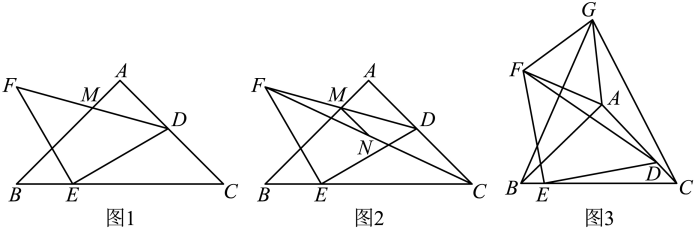 (1)、如图1,当时,若 , 求的长;(2)、如图2,连接 , 为的中点,连接 , 求证:;(3)、如图3,连接 , 将绕点A顺时针旋转得 , 连接、、 , 若 , 当周长取得最小值时,直接写出的面积.
(1)、如图1,当时,若 , 求的长;(2)、如图2,连接 , 为的中点,连接 , 求证:;(3)、如图3,连接 , 将绕点A顺时针旋转得 , 连接、、 , 若 , 当周长取得最小值时,直接写出的面积.