江苏省宿迁市泗洪县2023年一模数学试题

试卷更新日期：2023-03-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2023的相反数等于（）

A、2023 B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 计算（-a）²·a³的结果是（）

A、a⁶ B、-a⁶ C、-a⁵ D、a⁵

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是( )

A、正六边形 B、正五边形 C、平行四边形 D、等腰三角形

查看试题解析
4. 下列表示东台某天早晨、中午和午夜的温度（单位：℃），则下列说法正确的是（）

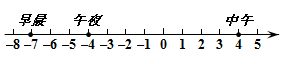A、午夜与早晨的温差是11℃ B、中午与午夜的温差是0℃ C、中午与早晨的温差是11℃ D、中午与早晨的温差是3℃

查看试题解析
5. 如图，在正方形网格中， $△ A B C$ 的顶点均在格点上，则 $t a n A$ 的值为（）

A、 $\frac{\sqrt{10}}{3}$ B、 $\frac{3 \sqrt{10}}{10}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
6. 甲、乙两班的数学平均成绩分别为72分和77分，现在，小明同学从乙班调到甲班，调动后再计算，结果两班成绩都有所上升，则小明同学此次数学成绩可能是（）

A、62分 B、72分 C、75分 D、85分

查看试题解析
7. 若点 $A (- 1 ， y_{1}) ， B (1 ， y_{2}) ， C (3 ， y_{3})$ 在反比例函数 $y = \frac{2}{x}$ 的图像上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ A = 30 ° ， B C = 4$ .将 $△ A B C$ 绕顶点C旋转得到 $△ A^{'} B^{'} C$ ，若点O是 $B C$ 中点，点P是 $A^{'} B^{'}$ 中点，在旋转过程中，线段 $O P$ 的最大值等于（）

A、4 B、6 C、8 D、10

查看试题解析

二、填空题

9. 计算： $2 + (- 3) =$ .

查看试题解析
10. 不等式组 ${\begin{array}{l} x + 1 < 2 \\ 2 x + 5 \geq 1 \end{array}$ 的解集是.

查看试题解析
11. 若 $2 x^{2} - 18 = 2 (x + 3) (x + a)$ ，则 $a =$ .

查看试题解析
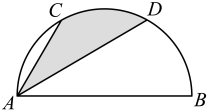
12. 某种微生物半径约为0.00000637米，将0.00000637米用科学记数法可表示为米.

查看试题解析
13. 直线y=-2x+3不经过第象限.

查看试题解析
14. 抛掷一枚质地均匀的骰子一次，朝上一面的点数是2的倍数的概率是.

查看试题解析
15. 已知 $△ A B C$ 三条中位线的长分别为3、4、5，则该三角形的面积为.

查看试题解析
16. 关于x的方程 $x^{2} + m x + n = 0$ 的两个根分别是 $\sqrt{2} + 1 ， \sqrt{2} - 1$ ，则 $m + n =$ .

查看试题解析
17. 如图，半圆的直径 $A B = 40$ ，若C、D是半圆的3等分点，则阴影部分的面积为.（结果保留π）

查看试题解析
18. 如图，抛物线 $y = x^{2} + 2 x - 3$ 交x轴于A、B两点.点P为x轴下方抛物线上任意一点，点C是抛物线对称轴与x轴的交点，直线 $B P 、 A P$ 分别交抛物线的对称轴于点M、N. $C M + C N$ 的值等于.

查看试题解析

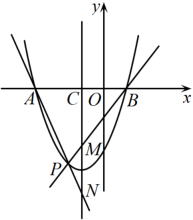
三、解答题

19. 计算： $| - \sqrt{3} | + (2 - π)^{0} - 2 c o s 60 °$ .

查看试题解析
20. 化简： $\frac{2 a}{a^{2} - 4} \cdot \frac{a - 2}{a} + \frac{a}{a + 2}$ .

查看试题解析
21. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，点D是 $\overset{⌢}{A C}$ 的中点，弦 $B D$ 交 $A C$ 于点E. $△ C D E$ 与 $△ B D C$ 相似吗？为什么？

查看试题解析
22. 为了解学生每周阅读课外书籍用时情况，兴趣小组从全校 $1200$ 名学生中随机选取一部分学生进行调查，调查分为A：总用时 $\leq 1$ 小时；B：1小时 $<$ 总用时 $\leq 4$ 小时；C：4小时 $<$ 总用时 $\leq 7$ 小时；D：总用时 $>$ 7小时.统计结果制成了如图两幅统计图：

(1)、本次抽查样本容量是；

(2)、请将条形统计图补全；

(3)、全校每周阅读课外书籍总用时超过7小时的学生大约有多少人？

查看试题解析
23. 如图，梯形 $A B C D$ 是某水坝的横截面示意图，其中 $A B = C D$ ，坝顶 $B C = 2 m$ ，坝高 $C H = 5 m$ ，迎水坡 $A B$ 的坡度为 $i = 1 ： 1$ .

(1)、求坝底 $A D$ 的长；

(2)、为了提高堤坝防洪抗洪能力，防汛指挥部决定在背水坡加固该堤坝，要求坝顶加宽 $0.5 m$ ，背水坡坡角改为 $α = 30 °$ .求加固总长5千米的堤坝共需多少土方？（参考数据： $π \approx 3.14 ， \sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ；结果精确到 $0.1 m^{3}$ ）

查看试题解析
24. 甲、乙两个不透明的袋子中各有三种颜色的小球若干颗，这些小球除颜色外其他都同，具体情况如下表所示：
颜色袋子
红色
白色
黑色
合计
甲袋
2颗
1颗
2颗
5颗
乙袋
1颗
2颗
1颗
4颗

(1)、填空：从甲袋中摸出一颗小球是红色的概率是；

(2)、求：从甲、乙两袋中各摸出一颗小球，颜色相同的概率.

查看试题解析
25. 为弘扬勤俭美德，落实节约政策，某旅游景点进行设施改造，将手动水龙头全部换成感应水龙头.已知改造完成后，平均每天的用水量减少 $\frac{1}{5}$ ， 48吨水可以比原来多用6天，该景点在实施改造后平均每天用水多少吨？

查看试题解析
26. 已知，点D是 $∠ C A B$ 的边 $A B$ 上一点.

(1)、如图甲， $D E ⊥ A C$ ，垂足为E， $D F$ 平分 $∠ A D E$ 交边 $A C$ 于点F， $F O ⊥ A C$ 交边 $A B$ 于点O，求证： $O D = O F$ ；

(2)、如图乙， $D E ⊥ A B$ 交边 $A C$ 于点E， $E O$ 平分 $∠ A E D$ 交边 $A B$ 于点O， $O F ⊥ A C$ ，垂足为点F，求证： $△ O E D ≌ △ O E F$ ；

(3)、如图丙，在线段 $A D$ 上找一点O作 $⊙ O$ ，使 $⊙ O$ 经过点D且与 $A C$ 相切.（要求：尺规作图，保留作图痕迹，写出作法过程，不证明）

查看试题解析
27. 已知抛物线 $y = a x^{2} + 2 a x + 3 a^{2} - 4 (a \neq 0)$ .

(1)、求这条抛物线的对称轴；

(2)、若该抛物线的顶点在x轴上，求其函数的表达式；

(3)、设该抛物线上有两点 $A (m ， y_{1}) 、 B (3 ， y_{2})$ ，若 $y_{1} < y_{2}$ ，求m的取值范围.

查看试题解析
28. 已知四边形 $A B C D$ 是边长为1的正方形，点E是边 $B C$ 上的动点，以 $A E$ 为直角边在直线 $B C$ 的上方作等腰直角三角形 $A E F ， ∠ A E F = 90 ° ， E F 、 A F$ 与 $C D$ 分别相交于点P、Q，连接 $E Q$ ，过点A作 $A M ⊥ E Q$ ，垂足为点M，过点P作 $P N ⊥ E Q$ ，垂足为点N，设 $B E = m$ .

(1)、求 $A M$ 的长；

(2)、用含有m的代数式表示 $C Q$ ；

(3)、用含有m的代数式表示 $P N$ ，并求 $P N$ 的最大值.

查看试题解析

颜色袋子	红色	白色	黑色	合计
甲袋	2颗	1颗	2颗	5颗
乙袋	1颗	2颗	1颗	4颗