湖南省岳阳汨罗市弼时片2023年九年级下学期第一次联考数学试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 下列实数中是无理数的是( )A、3.14 B、 C、-1 D、2. 在下面的四个几何体中,它们各自的三视图相同的是( )A、
 B、
B、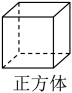 C、
C、 D、
D、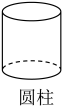 3. 下列运算结果正确的是( )A、 B、 C、 D、4. 某校九年级一班实施新课改以来,学生经常采用“小组合作学习”的方式进行学习,学习委员小玲每周对各小组合作学习的情况进行综合评分.如表是其中一周的统计数据,这组数据的中位数和众数分别是( )
3. 下列运算结果正确的是( )A、 B、 C、 D、4. 某校九年级一班实施新课改以来,学生经常采用“小组合作学习”的方式进行学习,学习委员小玲每周对各小组合作学习的情况进行综合评分.如表是其中一周的统计数据,这组数据的中位数和众数分别是( )组别
分数
A、 , B、 , C、 , D、 ,5. 如图,AB∥CD,∠1= , AF平分∠BAE,则∠2的度数为( ) A、 B、+15° C、+30° D、6. 下列命题是真命题的是( )A、菱形的对角线相等 B、直角三角形斜边上的中线等于斜边的一半 C、圆内接四边形对角相等 D、三角形的内心是三角形三条边的垂直平分线的交点7. 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两.请问:所分的银子共有( )两.(注:明代时1斤两,故有“半斤八两”这个成语)
A、 B、+15° C、+30° D、6. 下列命题是真命题的是( )A、菱形的对角线相等 B、直角三角形斜边上的中线等于斜边的一半 C、圆内接四边形对角相等 D、三角形的内心是三角形三条边的垂直平分线的交点7. 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两.请问:所分的银子共有( )两.(注:明代时1斤两,故有“半斤八两”这个成语) A、45 B、46 C、47 D、488. 将二次函数配成顶点式后,发现其顶点的纵坐标比横坐标大1,如图,在矩形中,点 , 点 , 则二次函数与矩形有交点时的取值范围是( )
A、45 B、46 C、47 D、488. 将二次函数配成顶点式后,发现其顶点的纵坐标比横坐标大1,如图,在矩形中,点 , 点 , 则二次函数与矩形有交点时的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 函数 中自变量x的取值范围是 .10. 分式方程的解为.11. 如图,在中, , , 按以下步骤作图:①分别以 , 为圆心,以大于的长为半径做弧,两弧相交于点和.②作直线交于点 , 交于点 , 连接.若 , 则.
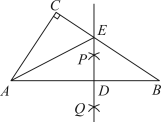 12. 已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是.13. 如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第个图案需棋子542枚.
12. 已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是.13. 如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第个图案需棋子542枚. 14. 在一个不透明的袋中装有2个黄球和2个红球,如果从袋中随机摸出一个球,然后放回搅匀,再从袋中随机摸出一个球,那么两次都摸到红球的概率是.15. 如图,同学们利用所学知识去测量三江源某河段某处的宽度,小童同学在A处观测对岸点C,测得 , 小郑同学在距点A处米远的B点测得 , 请计算:河宽米.(精确到米, , )
14. 在一个不透明的袋中装有2个黄球和2个红球,如果从袋中随机摸出一个球,然后放回搅匀,再从袋中随机摸出一个球,那么两次都摸到红球的概率是.15. 如图,同学们利用所学知识去测量三江源某河段某处的宽度,小童同学在A处观测对岸点C,测得 , 小郑同学在距点A处米远的B点测得 , 请计算:河宽米.(精确到米, , ) 16. 如图,已知是△ABC的外接圆,且圆心O在线段AB上,点D是上一点,DA的延长线与过点C的切线交于点E,且 , 连接CD交AB于点F,①若 , 的半径 , 则;②若 , 则.
16. 如图,已知是△ABC的外接圆,且圆心O在线段AB上,点D是上一点,DA的延长线与过点C的切线交于点E,且 , 连接CD交AB于点F,①若 , 的半径 , 则;②若 , 则.
三、解答题
-
17. 计算:.18. 先化简,再求值: , 其中是方程的解.19. 如图所示,点在四边形的边上,连接 , 并延长交的延长线于点 , 已知 , .
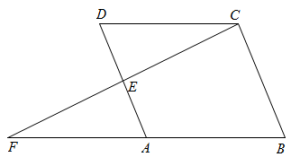 (1)、求证:;(2)、若 , 求证:四边形为平行四边形.20. 某校为了了解九年级学生周末在家体育锻炼情况,从九年级学生中随机抽取若干名学生进行调查,以下是根据调查数据绘制的部分统计图表和扇形统计图,根据信息回答下列问题:
(1)、求证:;(2)、若 , 求证:四边形为平行四边形.20. 某校为了了解九年级学生周末在家体育锻炼情况,从九年级学生中随机抽取若干名学生进行调查,以下是根据调查数据绘制的部分统计图表和扇形统计图,根据信息回答下列问题:等级等级
体育锻炼时间(分
人数
 (1)、本次调查共人,表中 ,(2)、扇形统计图中,“”所对应的扇形圆心角的度数为;(3)、若该校九年级共有名学生,请你估计周末体育锻炼超过分钟的学生人数.21. 如图,一次函数与反比例函数的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点.
(1)、本次调查共人,表中 ,(2)、扇形统计图中,“”所对应的扇形圆心角的度数为;(3)、若该校九年级共有名学生,请你估计周末体育锻炼超过分钟的学生人数.21. 如图,一次函数与反比例函数的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点. (1)、求反比例函数的解析式;(2)、连接OB,若△BOC的面积为3,求点A的坐标.22. 学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。(1)、分别求一本笔记本和一支钢笔的售价;(2)、若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。23. 如图①,在中, , , , D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上).
(1)、求反比例函数的解析式;(2)、连接OB,若△BOC的面积为3,求点A的坐标.22. 学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。(1)、分别求一本笔记本和一支钢笔的售价;(2)、若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。23. 如图①,在中, , , , D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上). (1)、计算矩形的面积;(2)、将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;(3)、如图③,将(2)中矩形平移停止时所得的矩形记为矩形 , 将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形 , 设旋转角为 , 求的值.24. 如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,直线过点B,与y轴交于点D,点C与点D关于x轴对称.点P是线段上一动点,过点P作x轴的垂线交抛物线于点M,交直线于点N.
(1)、计算矩形的面积;(2)、将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;(3)、如图③,将(2)中矩形平移停止时所得的矩形记为矩形 , 将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形 , 设旋转角为 , 求的值.24. 如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,直线过点B,与y轴交于点D,点C与点D关于x轴对称.点P是线段上一动点,过点P作x轴的垂线交抛物线于点M,交直线于点N. (1)、求抛物线的解析式;(2)、当的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q,使得以Q,M,N,D为顶点的四边形是平行四边形,若存在,求出点Q的坐标;若不存在;说明理由
(1)、求抛物线的解析式;(2)、当的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q,使得以Q,M,N,D为顶点的四边形是平行四边形,若存在,求出点Q的坐标;若不存在;说明理由