湖北省随州市2023年中考数学九年级第一次模拟考检测卷

试卷更新日期：2023-03-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的相反数的倒数是（）

A、2022 B、 $- \frac{1}{2022}$ C、 $\frac{1}{2022}$ D、 $- 2022$

查看试题解析
2. 2021年5月22日，中国工程院院士袁隆平在长沙不幸逝世.这位“共和国勋章获得者”的最大贡献是杂交水稻技术.2020年我国水稻种植面积4.5亿亩，其中50%左右是杂交水稻，则杂交水稻种植面积用科学记数法表示约为（）

A、 4.5×10⁸亩 B、2.25×10⁸亩 C、4.5×10⁹亩 D、2.25×10⁹亩

查看试题解析
3. 马大哈同学做如下运算题：①x⁵+x⁵＝x¹⁰②x⁵-x⁴＝x③x⁵•x⁵＝x¹⁰④x¹⁰÷x⁵＝x²⑤（x⁵）²＝x²⁵ ，其中结果正确的是（）

A、①②④ B、②④ C、③ D、④⑥

查看试题解析
4. 如图所示的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，AC＝10，则CD的长度是（）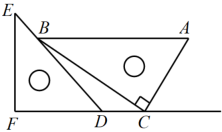

A、5 B、 $5 \sqrt{3}$ C、10- $5 \sqrt{3}$ D、15- $5 \sqrt{3}$

查看试题解析
6. 已知a，b，c分别是Rt△ABC的三条边长，c为斜边长， $∠ C = 90 °$ ，我们把关于x的形如 $y = \frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”.若点 $P (1 ， \frac{\sqrt{3}}{3})$ 在“勾股一次函数”的图象上，且 $R t △ A B C$ 的面积是4，则c的值是（）

A、 $2 \sqrt{6}$ B、24 C、 $2 \sqrt{3}$ D、12

查看试题解析
7. 将方程 $2 (x - 1) = 3 (x - 1)$ 的两边同除以 $(x - 1)$ ，将 $2 = 3$ ，其错误的原因是（）

A、方程本身是错的 B、方程无解 C、两边都除以0 D、 $2 (x - 1)$ 小于 $3 (x - 1)$

查看试题解析
8. 如图，在菱形ABCD中，AB=4，∠C=60°，将菱形折叠，使点A恰好落在对角线BD上的G点处（不与B，D重合），折痕为EF，若DG= $\frac{1}{3}$ BG，则BE的长为（）

A、 $\frac{14}{5}$ B、 $\frac{13}{5}$ C、 $\frac{13}{7}$ D、 $\frac{7}{5}$

查看试题解析
9. 看了《田忌赛马》故事后，数学兴趣小组用数学模型来分析：齐王与田忌的上中下三个等级的三匹马综合指标数如表，每匹马只赛一场，综合指标的两数相比，大数为胜，三场两胜则赢，已知齐王的三匹马出场顺序为6、4、2，若田忌的三匹马随机出场，则田忌能赢得比赛的概率为（）
马匹等级
下等马
中等马
上等马
齐王
2
4
6
田忌
1
3
5

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{12}$

查看试题解析
10. 如图，等边三角形ABC， $A B = 6$ ， D为BC中点，M为AD上的动点，连接CM，将线段CM绕点C逆时针方向旋转60°得到CN，连接ND，则 $N D + C N$ 的最小值为（）

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、6

查看试题解析

二、填空题

11. 计算： $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}} - 2^{- 1} + t a n^{2} 3 0^{°}$ ＝.

查看试题解析
12. 生活中到处可见黄金分割的美.向日葵就是一个很好的例子，如果仔细观察向日葵中心，就会发现似乎有条螺旋形的曲线，如果对此进行计算，结果会得到黄金分割数列，如图是一株向日葵的俯视图，点C分线段AB近似于黄金分割（黄金分割比≈0.618）.已知AC＝2，且AC＞BC，则BC的长约 .

查看试题解析
13. 如图，AB是半圆的直径，C为半圆上一点，BC，D为弧BC上一点.连接OD，连接AE，若四边形ACDE为平行四边形，AE=2 $\sqrt{3}$ ，则AB的长为.

查看试题解析
14. 已知二次函数 $y = (m - 2) x^{2} + 2 m x + m - 3$ 的图象与x轴有两个交点 $(x_{1} ， 0) ， (x_{2} ， 0)$ ，则下列说法在确的有：.（填序号）
①该二次函数的图象一定过定点 $(- 1 ， - 3)$ ；
②若该函数图象开口向下，则m的取值范围为： $\frac{6}{5} < m < 2$ ；
③当 $m > 2$ 且 $0 ⩽ x ⩽ 2$ 时，y的最小值为 $m - 3$ ；
④当 $m > 2$ ，且该函数图象与x轴两交点的横坐标 $x_{1} 、 x_{2}$ 满足 $- 4 < x_{1} < - 3 ， - 1 < x_{2} < 0$ 时，m的取值范围为： $\frac{35}{9} < m < \frac{21}{4}$ .

查看试题解析

三、解答题

15.

(1)、解方程：x²+x﹣6＝0；

(2)、解不等式组： ${\begin{matrix} 3 x + 6 \geq 5 (x - 2) \\ \frac{x - 5}{2} - \frac{4 x - 3}{3} < 1 \end{matrix}$ .

查看试题解析
16. 如图，在边长为1的正方形组成的网格中建立直角坐标系， $△ A O B$ 的顶点均在格点上，点 $O$ 为原点，点 $A$ ， $B$ 的坐标分别是 $A (3 ， 2)$ ， $B (1 ， 3)$ .

(1)、若将 $△ A O B$ 向下平移3个单位，则点B的对应点坐标为；

(2)、将 $△ A O B$ 绕点 $O$ 逆时针旋转 $9 0^{°}$ 后得到 $△ A_{1} O B_{1}$ ，请在图中作出 $△ A_{1} O B_{1}$ ，并求出这时点 $A_{1}$ 的坐标；

(3)、求旋转过程中，线段 $O A$ 扫过的图形的弧长.

查看试题解析
17. 某沿海城市O，每年都会受到几次台风侵袭，台风是一种自然灾害，它以台风中心为圆心在数十千米范围内形成气旋风景，有极强的破坏力.某次，据气象观察，距该城市正南方向的A处有一台风中心，中心最大风力为12级，每远离台风中心 $\frac{100}{3}$ 千米，风力就会减弱一级，该台风中心正以20千米/时的速度沿北偏东45°方向向B处移动，且台风中心风力不变，若城市受到风力达到或超过6级，则称受台风影响.

(1)、若该城市受此次台风影响共持续了10小时（即台风中心从C处移动到D处），那么受到台风影响的最大风力为几级?

(2)、求该城市O到A处的距离.（注：结果四舍五入保留整数，参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ）

查看试题解析
18. 观察一下等式：
第一个等式： $\frac{1}{2} = 1 - \frac{1}{2}$ ，
第二个等式： $\frac{1}{2} + \frac{1}{2^{2}} = 1 - \frac{1}{2^{2}}$ ，
第三个等式： $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} = 1 - \frac{1}{2^{3}}$ ， ……
按照以上规律，解决下列问题

(1)、 $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} = 1 -$ ；

(2)、写出第五个式子：；

(3)、用含的式子表示一般规律： $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \dots + \frac{1}{2^{n}} = 1 -$ ；

(4)、计算（要求写出过程）： $\frac{3}{2} + \frac{3}{2^{2}} + \frac{3}{2^{3}} + \frac{3}{2^{4}} + \frac{3}{2^{5}} + \frac{3}{2^{6}}$ .

查看试题解析

19. 距离2022年中招体育考试的时间已经越来越近，某校初三年级为了了解本校学生在平时体育训练的效果，随机抽取了男、女各60名考生的体考成绩，并将数据进行整理分析，给出了下面部分信息：
数据分为A，B，C，D四个等级分别是：
A：48≤x≤50，B：45≤x＜48，C：40≤x＜45，D：0≤x＜40

60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：
男生成绩在B组的前10名考生的分数为：
47.5，47.5，47.5，47，47，47，46，45.5，45，45.

60名男生和60名女生成绩的平均数，中位数，众数如下：

性别	平均数	中位数	众数
男生	47.5	a	47
女生	47.5	47	47.5

根据以上信息，解答下列问题：

(1)、填空：

a =

▲ ，

b =

▲ ，并补全条形统计图.

(2)、根据以上数据，你认为在此次考试中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）.

(3)、若该年级有800名学生，请估计该年级所有参加体考的考生中，成绩为A等级的考生人数.

查看试题解析

20. 如图，在平面直角坐标系中，点 $O$ 为坐标系原点，矩形 $O A B C$ 的边 $O A$ ， $O C$ 分别在 $x$ 轴和 $y$ 轴上，其中 $c o s ∠ O B C = \frac{4}{5}$ ， $O C = 3$ .已知反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过 $B C$ 边上的中点 $D$ ，交 $A B$ 于点 $E$ .

(1)、求 $k$ 的值；

(2)、猜想 $Δ O C D$ 的面积与 $Δ O B E$ 的面积之间的关系，请说明理由.

(3)、若点 $P (x ， y)$ 在该反比例函数的图象上运动（不与点 $D$ 重合），过点 $P$ 作 $P R ⊥ y$ 轴于点 $R$ ，作 $P Q ⊥ B C$ 所在直线于点 $Q$ ，记四边形 $C Q P R$ 的面积为 $S$ ，求 $S$ 关于 $x$ 的解析式并写出 $x$ 的取值范围.

查看试题解析
21. 如图1，CD是 $⊙ O$ 的弦，半径 $O A ⊥ C D$ ，垂足为B，过点C作 $⊙ O$ 的切线l.

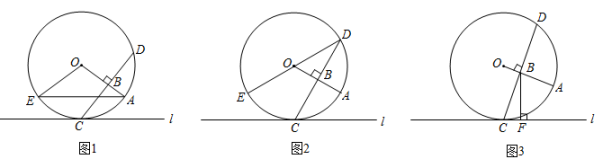(1)、若点E在 $⊙ O$ 上，且 $\overset{⌢}{C E} = \overset{⌢}{C A}$ ，连接OE.
①连接AE，求证： $A E ∥ l$ ；
②如图2，若B是OA的中点，连接OD，求证：DE是 $⊙ O$ 的直径；

(2)、如图3，过点B作 $B F ⊥ l$ ，垂足为F，若 $⊙ O$ 的半径是4，求 $B C - B F$ 的最大值.

查看试题解析
22. 如图，在正方形 $A B C D$ 中，点E在直线 $A D$ 右侧，且 $A E = 1$ ，以 $D E$ 为边作正方形 $D E F G$ ，射线 $D F$ 与边 $B C$ 交于点M，连接 $M E$ 、 $M G$ .

(1)、如图1，求证： $M E = M G$ ；

(2)、若正方形 $A B C D$ 的边长为4，
①如图2，当G、C、M三点共线时，设 $E F$ 与 $B C$ 交于点N，求 $\frac{M N}{E M}$ 的值；
②如图3，取 $A D$ 中点P，连接 $P F$ ，求 $P F$ 长度的最大值.

查看试题解析
23. 抛物线 $y = x^{2} - 1$ 交 $x$ 轴于 $A$ ， $B$ 两点（ $A$ 在 $B$ 的左边）.

(1)、 $▱ A C D E$ 的顶点 $C$ 在 $y$ 轴的正半轴上，顶点 $E$ 在 $y$ 轴右侧的抛物线上.
①如图（1），若点 $C$ 的坐标是 $(0 ， 3)$ ，点 $E$ 的横坐标是 $\frac{3}{2}$ ，直接写出点 $A$ ， $D$ 的坐标；

②如图（2），若点 $D$ 在抛物线上，且 $▱ A C D E$ 的面积是12，求点 $E$ 的坐标；

(2)、如图（3）， $F$ 是原点 $O$ 关于抛物线顶点的对称点，不平行 $y$ 轴的直线 $l$ 分别交线段 $A F$ ， $B F$ （不含端点）于 $G$ ， $H$ 两点，若直线 $l$ 与抛物线只有一个公共点，求证 $F G + F H$ 的值是定值.

查看试题解析

马匹等级	下等马	中等马	上等马
齐王	2	4	6
田忌	1	3	5