河南省洛阳市偃师市2023年中考数学一模试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 计算的值等于( )A、 B、 C、 D、2. 下列正确的是()A、 B、 C、 D、3. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、4. 如图,已知 , 那么添加下列的一个条件后,仍无法判定的是( )
 A、 B、 C、 D、5. 如图,是的高.若 , , 则边的长为( )
A、 B、 C、 D、5. 如图,是的高.若 , , 则边的长为( ) A、 B、 C、 D、6. 某种服装平均每天可销售20件,每件盈利44元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件,如果每天要盈利1600元,每件降价多少元?设每件降价x元,则可列方程为( )A、 B、 C、 D、7. 课外活动课上,小明用矩形ABCD玩折纸游戏,如图,第一步,把矩形ABCD沿EF对折,折出折痕EF,并展开;第二步,将纸片折叠,使点A落在EF上点,若 , 则折痕BG的长等于( )
A、 B、 C、 D、6. 某种服装平均每天可销售20件,每件盈利44元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件,如果每天要盈利1600元,每件降价多少元?设每件降价x元,则可列方程为( )A、 B、 C、 D、7. 课外活动课上,小明用矩形ABCD玩折纸游戏,如图,第一步,把矩形ABCD沿EF对折,折出折痕EF,并展开;第二步,将纸片折叠,使点A落在EF上点,若 , 则折痕BG的长等于( ) A、 B、 C、 D、8. 甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
A、 B、 C、 D、8. 甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) A、抛一枚硬币,连续两次出现正面的概率 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、任意写一个正整数,它能被5整除的概率 D、掷一枚正六面体的骰子,出现1点的概率9. 如图,点是的重心,和是以点为位似中心的位似图形.则与的面积之比为( )
A、抛一枚硬币,连续两次出现正面的概率 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、任意写一个正整数,它能被5整除的概率 D、掷一枚正六面体的骰子,出现1点的概率9. 如图,点是的重心,和是以点为位似中心的位似图形.则与的面积之比为( ) A、 B、 C、 D、10. 如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形 ;第二次,顺次连接四边形 各边的中点,得到四边形 ;…如此反复操作下去,则第n次操作后,得到四边形 的面积是( )
A、 B、 C、 D、10. 如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形 ;第二次,顺次连接四边形 各边的中点,得到四边形 ;…如此反复操作下去,则第n次操作后,得到四边形 的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
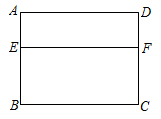
11. 比较大小:(填“”,“”或“” .12. 关于 的一元二次方程 的一个根是3,则另一个根是.13. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.
 14. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
14. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .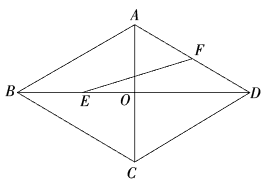 15. 如图,在平面直角坐标系中.边长为的等边的边在轴上,、、分别是、、上的动点,且满足 , , 连接、 , 当点坐标为时,与相似.
15. 如图,在平面直角坐标系中.边长为的等边的边在轴上,、、分别是、、上的动点,且满足 , , 连接、 , 当点坐标为时,与相似.
三、解答题
-
16. 计算:(1)、;(2)、.17. 解方程:(1)、;(2)、18. 某医院计划选派护士支援某地的防疫工作,甲、乙、丙、丁4名护士积极报名参加,其中甲是共青团员,其余3人均是共产党员.医院决定用随机抽取的方式确定人选.(1)、“随机抽取1人,甲恰好被抽中”是____事件;A、不可能 B、必然 C、随机(2)、若需从这4名护士中随机抽取2人,请用画树状图法或列表法求出被抽到的两名护士都是共产党员的概率.19. 如图,在中,点 , , 分别在边 , , 上,连接 , 已知四边形是平行四边形,

 (1)、若 , 求线段的长.(2)、若的面积为 , 求平行四边形的面积.20. 已知关于x的一元二次方程有实数根.(1)、求实数k的取值范围.(2)、设方程的两个实数根分别为 , 若 , 求k的值.21. 在中, , 是边上的中线,过点作的垂线交的延长线于点 , 于点.
(1)、若 , 求线段的长.(2)、若的面积为 , 求平行四边形的面积.20. 已知关于x的一元二次方程有实数根.(1)、求实数k的取值范围.(2)、设方程的两个实数根分别为 , 若 , 求k的值.21. 在中, , 是边上的中线,过点作的垂线交的延长线于点 , 于点. (1)、求证:平分;(2)、求证:.22. 如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向,AC=200米.点E在点A的正北方向.点B,D在点C的正北方向,BD=100米.点B在点A的北偏东30°,点D在点E的北偏东45°.
(1)、求证:平分;(2)、求证:.22. 如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向,AC=200米.点E在点A的正北方向.点B,D在点C的正北方向,BD=100米.点B在点A的北偏东30°,点D在点E的北偏东45°.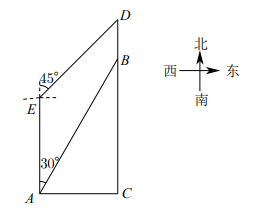 (1)、求步道DE的长度(精确到个位);(2)、点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?(参考数据:23.(1)、【基础巩固】如图1,在中,D,E,F分别为 , , 上的点, , , 交于点G,求证:.
(1)、求步道DE的长度(精确到个位);(2)、点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?(参考数据:23.(1)、【基础巩固】如图1,在中,D,E,F分别为 , , 上的点, , , 交于点G,求证:.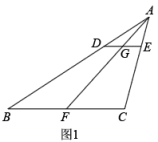 (2)、【尝试应用】如图2,在(1)的条件下,连接 , .若 , , , 求的值.
(2)、【尝试应用】如图2,在(1)的条件下,连接 , .若 , , , 求的值. (3)、【拓展提高】如图3,在中, , 与交于点O,E为上一点,交于点G,交于点F.若 , 平分 , , 求的长.
(3)、【拓展提高】如图3,在中, , 与交于点O,E为上一点,交于点G,交于点F.若 , 平分 , , 求的长.