海南省琼中县2023年中考数学一模试题
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题
-
1. 若非零数 , 互为相反数,下列四组数中,互为相反数的个数为( )
①与;②与;③与;④与
A、0 B、1 C、2 D、32. 在一项科学研究中,科学家对人体血液中尺寸小于0.000508毫米的微小颗粒进行分析,发现在部分血液样本中含有“微塑料”颗粒,这是科学家首次在人类血液中检测到“微塑料”污染.我们可以把数据“0.000508”用科学记数法表示为( )A、5.08×10-5 B、5.08×10-4 C、50.8×10-5 D、508×10-63. 如图中几何体从正面看能得到( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 将不等式的解集表示在数轴上,正确的是( )A、
4. 将不等式的解集表示在数轴上,正确的是( )A、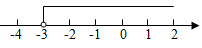 B、
B、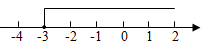 C、
C、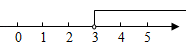 D、
D、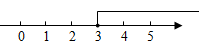 5. 下列命题中,真命题是( )A、相等的角是对顶角 B、在同一平面内,垂直于同一条直线的两条直线平行 C、两条直线被第三条直线所截,同位角相等 D、同旁内角互补6. 某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是( )A、众数是3 B、中位数是0 C、平均数是3 D、极差是57. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是( )A、1 B、2 C、4 D、68. 如图,在矩形中, , 将矩形绕点A逆时针旋转得到矩形 , 点B的对应点落在上,且 , 则四边形的面积为( ).
5. 下列命题中,真命题是( )A、相等的角是对顶角 B、在同一平面内,垂直于同一条直线的两条直线平行 C、两条直线被第三条直线所截,同位角相等 D、同旁内角互补6. 某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是( )A、众数是3 B、中位数是0 C、平均数是3 D、极差是57. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是( )A、1 B、2 C、4 D、68. 如图,在矩形中, , 将矩形绕点A逆时针旋转得到矩形 , 点B的对应点落在上,且 , 则四边形的面积为( ). A、 B、 C、 D、9. 若反比例函数的图象经过点 , 则下列各点中也在这个函数图象的是( )A、 B、 C、 D、10. 等腰三角形一腰上的高与另一腰的夹角为 , 则等腰三角形的底角度数为( )A、 B、 C、或 D、或11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A、 B、 C、 D、9. 若反比例函数的图象经过点 , 则下列各点中也在这个函数图象的是( )A、 B、 C、 D、10. 等腰三角形一腰上的高与另一腰的夹角为 , 则等腰三角形的底角度数为( )A、 B、 C、或 D、或11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( ) A、 B、8 C、 D、612. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )
A、 B、8 C、 D、612. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )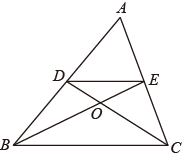 A、6 B、9 C、12 D、13.5
A、6 B、9 C、12 D、13.5二、填空题
-
13. 分解因式:.14. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 .
 15. 如图,在 的内部有一点 ,点 、 分别是点 关于 , 的对称点, 分别交 , 于 , 点,若 的周长为 ,则线段 的长为 .
15. 如图,在 的内部有一点 ,点 、 分别是点 关于 , 的对称点, 分别交 , 于 , 点,若 的周长为 ,则线段 的长为 .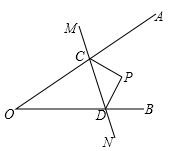 16. 用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为.
16. 用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为.
三、解答题
-
17. 计算下列各题:(1)、(2)、.18. 我市在创建省级卫生文明城市建设中,对城内的部分河道进行整治.现有一段长360米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治16米,乙工程队每天整治24米,共用时20天.求甲、乙两工程队分别整治河道多少米?(1)、小明、小华两位同学提出的解题思路如下:
①小明同学:设整治任务完成后单工程队整治河道米,乙工程队整治河道米.
根据题意,得
②小华同学:设整治任务完成后,表示 ▲ , 表示 ▲ ;
则可列方程组为
请你补全小明、小华两位同学的解题思路.
(2)、请从①②中任选一个解题思路,写出完整的解答过程.19. 为了提高学生的计算能力,某校举行了数学计算比赛,现从七八年级中各随机抽取15名学生的数学成绩(百分制)进行整理、描述和分析.(成绩得分用x表示,共分成4组:A. , B. , C. , D.)下面给出部分信息:
七年级学生的数学成绩在C组中的数据为:83,84,89.
八年级抽取的学生数学成绩:68,77,76,100,81,100,82,86,98,90,100,86,84,93,87.
七,八年抽取的学生数学成绩统计表
年级
平均数
中位数
众数
方差
七
87
a
98
八
86
b
 (1)、填空: , .(2)、根据以上数据,你认为该校七,八年中哪个年级学生计算能力较好?请说明理由(一条理由即可);(3)、该校七,八年共2500人参加了此次竞赛活动,请你估计参加此次竞赛活动成绩达到90分及以上的学生约有多少人?20. 为测量某机场东西两栋建筑物A、B之间的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,的距离为2千米,然后沿着平行于的方向飞行6.4千米到点D处,测得建筑物B的俯角为37°.(参考数据:).
(1)、填空: , .(2)、根据以上数据,你认为该校七,八年中哪个年级学生计算能力较好?请说明理由(一条理由即可);(3)、该校七,八年共2500人参加了此次竞赛活动,请你估计参加此次竞赛活动成绩达到90分及以上的学生约有多少人?20. 为测量某机场东西两栋建筑物A、B之间的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,的距离为2千米,然后沿着平行于的方向飞行6.4千米到点D处,测得建筑物B的俯角为37°.(参考数据:). (1)、无人机距离地面的飞行高度是多少千米?(2)、求该机场东西两栋建筑物A、B之间的距离.(结果精确到0.01千米)21. 【问题呈现】阿基米德折弦定理:阿基米德 , 公元前公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.如图1,和是的两条弦(即折线是圆的一条折弦), , 点是的中点,则从向所作垂线的垂足是折弦的中点,即.下面是运用“截长法”证明的部分证明过程.
(1)、无人机距离地面的飞行高度是多少千米?(2)、求该机场东西两栋建筑物A、B之间的距离.(结果精确到0.01千米)21. 【问题呈现】阿基米德折弦定理:阿基米德 , 公元前公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.如图1,和是的两条弦(即折线是圆的一条折弦), , 点是的中点,则从向所作垂线的垂足是折弦的中点,即.下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取 , 连接、、和.

是的中点,
,
又 , ,
,
,
又 ,
,
即.
(1)、【理解运用】如图1,、是的两条弦, , , 点M是的中点,于点D,则; (2)、【变式探究】如图3,若点M是的中点,【问题呈现】中的其他条件不变,判断、、之间存在怎样的数量关系?并加以证明.
(2)、【变式探究】如图3,若点M是的中点,【问题呈现】中的其他条件不变,判断、、之间存在怎样的数量关系?并加以证明. (3)、【实践应用】如图4,是的直径,点A圆上一定点,点D圆上一动点,且满足 , 若 , 的半径为5,则AD=.
(3)、【实践应用】如图4,是的直径,点A圆上一定点,点D圆上一动点,且满足 , 若 , 的半径为5,则AD=. 22. 如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(-2,0)和点B,与y轴交于点C(0,8),顶点为D,连接AC,CD,DB,直线BC与抛物线的对称轴l交于点E.
22. 如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(-2,0)和点B,与y轴交于点C(0,8),顶点为D,连接AC,CD,DB,直线BC与抛物线的对称轴l交于点E. (1)、求抛物线的解析式和直线BC的解析式;(2)、求四边形ABDC的面积;(3)、P是第一象限内抛物线上的动点,连接PB,PC,当S△PBCS△ABC时,求点P的坐标;(4)、在抛物线的对称轴l上是否存在点M,使得△BEM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和直线BC的解析式;(2)、求四边形ABDC的面积;(3)、P是第一象限内抛物线上的动点,连接PB,PC,当S△PBCS△ABC时,求点P的坐标;(4)、在抛物线的对称轴l上是否存在点M,使得△BEM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.