广西柳州市城中区2022-2023学年九年级下学期2月教学质量抽测数学试题

试卷更新日期：2023-03-24 类型：月考试卷

进入出卷网下载

一、单选题

1. －3的相反数是（）

A、3 B、－3 C、 $\pm 3$ D、 $- \frac{1}{3}$

查看试题解析
2. 下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，数据67500用科学记数法表示为（）

A、 $6.75 \times 1 0^{3}$ B、 $6.75 \times 1 0^{4}$ C、 $67.5 \times 1 0^{5}$ D、 $67.5 \times 1 0^{4}$

查看试题解析
4. 关于 $x$ 的一元一次不等式组的解集在数轴上表示如图，则这个不等式组的解集为（）

A、 $- 3 \leq x \leq 2$ B、 $- 3 < x \leq 2$ C、 $- 3 \leq x < 2$ D、 $- 3 < x < 2$

查看试题解析
5. 如图，在平面直角坐标系中，△ABC关于直线m（直线m上各点的横坐标都为1）对称，点C的坐标为（4，1），则点B的坐标为（）

A、（-2，1） B、（-3，1） C、（-2，-1） D、（2，1）

查看试题解析
6. 下列事件是随机事件的是（）

A、射击运动员射击一次，命中靶心 B、在标准大气压下，通常加热到 $100 ℃$ 时，水沸腾 C、任意画一个三角形，其内角和等于 $180 °$ D、在空旷的操场，向空中抛一枚硬币，硬币不会从空中落下

查看试题解析
7. 如图是小明学习“探索直线平行的条件”时用到的学具，经测量 $∠ 2 = 105 °$ ，要使木条a与b平行，则 $∠ 1$ 的度数应为（）

A、45° B、75° C、105° D、135°

查看试题解析
8. 下列运算中，正确的是（）

A、3x+4y＝12xy B、x⁹÷x³＝x³ C、（x²）³＝x⁶ D、（x-y）²＝x²-y²

查看试题解析
9. 如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的点中任取一点C，使△ABC为直角三角形的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{4}{7}$ D、 $\frac{3}{7}$

查看试题解析
10. 一次函数y＝kx＋b（k，b为常数，且k≠0）的图像如图所示，根据图像信息可求得关于x的方程kx＋b＝0的解为（）

A、x＝－1 B、x＝2 C、x＝0 D、x＝3

查看试题解析
11. 如图，两个正方形边长分别为a，b，已知 $a + b = 7$ ， $a b = 9$ ，则阴影部分的面积为（）

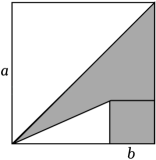A、10 B、11 C、12 D、13

查看试题解析
12. 如图，在△ABC中，BC的垂直平分线分别交AC，BC于点D，E.若△ABC的周长为24，CE＝4，则△ABD的周长为（）

A、16 B、18 C、20 D、24

查看试题解析

二、填空题

13. 若分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
14. 分解因式： $a b - a =$ .

查看试题解析
15. 如图，BD是⊙O的直径，点A、C在圆周上，∠CBD=20°，则∠A的度数为 °.

查看试题解析
16. 下表记录了一名球员在罚球线上投篮的结果．
投篮次数 $n$
50
100
150
200
300
400
500
投中次数 $m$
28
49
78
102
153
208
255
投中频率 $\frac{m}{n}$
0.56
0.49
0.52
0.51
0.51
0.52
0.51
根据以上数据，估计这名球员在罚球线上投篮一次，投中的概率为．

查看试题解析
17. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{3}{5}$ ， $A B = 10$ ，则 $A C$ 的长为.

查看试题解析
18. 如图所示，函数y=ax+b和y=|x|的图象相交于（﹣1，1），（2，2）两点．当y₁＞y₂时，x的取值范围是．

查看试题解析

三、解答题

19. 计算： $| - 2 | + {(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 1} + \sqrt[3]{- 8}$ .

查看试题解析
20. 先化简，再求值： $\frac{4}{m - 3}$ $\div$ $\frac{4 m}{m^{2} - 6 m + 9}$ ，其中 $m = 9$ .

查看试题解析
21. 如图，在平面直角坐标系内， $△ A B C$ 三个顶点的坐标分别为 $A (1 ， - 2)$ ， $B (4 ， - 1)$ ， $C (3 ， - 3)$ （正方形网格中，每个小正方形的边长都是1个单位长度）.

(1)、以坐标原点O为旋转中心，将 $△ A B C$ 逆时针旋转 $90 °$ ，得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、求点C到点 $C_{1}$ 经过的路径.

查看试题解析
22. 某中学组织七，八年学生参加了体质健康测试，现随机从七，八年各抽取了10名学生的成绩（单位：分），进行统计、分析.收集数据：
七年级：78，90，80，95，68，90，90，100，75，80；
八年级：80，70，85，95，90，100，90，85，90，78.
整理数据：
成绩x/分
$60 \leq x \leq 70$
$70 < x \leq 80$
$80 < x \leq 90$
$90 < x \leq 100$
七年级
1
4
3
2
八年级
1
2
a
b
分析数据：
统计量
平均数
中位数
众数
七年级
84.6
c
90
八年级
86.3
87.5
d

(1)、填空： $a =$ ， $b =$ ， $c =$ ， $d =$ ；

(2)、若八年级共有200人参与测试，请估计八年级成绩大于80分的人数；

(3)、根据以上数据，结合所学的统计知识，你认为哪个年级学生的体质更好，并说明理由（写出一条即可）.

查看试题解析
23. 如图，在△ABC中，CD平分∠ACB，CD的垂直平分线分别交AC、DC、BC于点E、F、G，连接DE、DG．

(1)、求证：四边形DGCE是菱形；

(2)、若∠ACB＝30°，∠B＝45°，ED＝6，求BG的长．

查看试题解析
24. 某文具店准备购甲、乙两种水笔进行销售，每支进价和利润如表：

甲水笔
乙水笔
每支进价（元）
a
$a + 5$
每支利润（元）
2
3
已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等.

(1)、求甲，乙两种水笔每支进价分别为多少元.

(2)、若该文具店准备拿出2000元全部用来购进这两种水笔，考虑顾客需求，要求购进甲种水笔的数量不超过乙种水笔数量的4倍，问该文具店如何进货能使利润最大，最大利润是多少元.

查看试题解析
25. 如图， $A B$ 是⊙O的直径，弦 $C D ⊥ A B$ ，垂足为H，E为 $\overset{⌢}{B C}$ 上一点，过点E作⊙O的切线，分别交 $D C ， A B$ 的延长线于点F，G，连接 $A E$ ，交 $C D$ 于点P.

(1)、求证： $E F = F P$ ；

(2)、连接 $A D$ ，若 $A D / / F G ， C D = 8 ， c o s F = \frac{4}{5}$ ，求 $E G$ 的长.

查看试题解析
26. 如图1，抛物线 $y = a x^{2} + b x + c$ 的图象与x轴交于 $A (- 3 ， 0) ， B (1 ， 0)$ 两点，与y轴交于点C，且 $O C = O A$ .

(1)、求抛物线解析式；

(2)、点M是直线 $A C$ 上方的抛物线上一动点，M点的横坐标为m，四边形 $A B C M$ 的面积为S，求S关于m的函数关系式，并求出S的最大值；

(3)、如图2， $D (0 ， - 2)$ ，连接 $B D$ ，将 $△ O B D$ 绕平面内的某点（记为P）逆时针旋转 $180 °$ 得到 $△ O^{'} B^{'} D^{'}$ ， O、B、D的对应点分别为 $O^{'} ， B^{'} ， D^{'}$ .若点 $B^{^{'}} ， D^{^{'}}$ 两点恰好落在抛物线上，求旋转中心点P的坐标.

查看试题解析

投篮次数 $n$	50	100	150	200	300	400	500
投中次数 $m$	28	49	78	102	153	208	255
投中频率 $\frac{m}{n}$	0.56	0.49	0.52	0.51	0.51	0.52	0.51

成绩x/分	$60 \leq x \leq 70$	$70 < x \leq 80$	$80 < x \leq 90$	$90 < x \leq 100$
七年级	1	4	3	2
八年级	1	2	a	b

统计量	平均数	中位数	众数
七年级	84.6	c	90
八年级	86.3	87.5	d

	甲水笔	乙水笔
每支进价（元）	a	$a + 5$
每支利润（元）	2	3