山东省济宁市泗水县2021-2022学年高二下学期数学期中考试试卷
试卷更新日期:2023-03-24 类型:期中考试
一、单选题
-
1. 下列求导运算中错误的是( )A、 B、 C、 D、2. 若函数的导函数为 , 且满足 , 则( )A、0 B、-1 C、-2 D、23. 若的展开式中,只有第6项的二项式系数最大,则该项式的展开式中常数项为( )A、90 B、-90 C、180 D、-1804. 中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有( )A、 种 B、 种 C、 种 D、 种5. 函数 的图像大致为( )A、
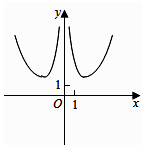 B、
B、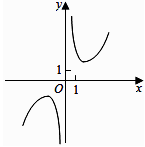 C、
C、 D、
D、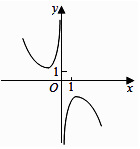 6. 已知曲线 在点 处的切线方程为 ,则( )A、 B、 C、 D、7. 埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,142857×4=571428,...,所以这组数字又叫“走马灯数”.该组数字还有如下发现:142+857=999,428+571=999,285+714=999,...,若从这组神秘数字中任选3个数字构成一个三位数 ,剩下的三个数字构成另一个三位数 ,若 ,则所有可能的有序实数组 的个数为( )A、48 B、60 C、96 D、1208. 已知的定义域为 , 为的导函数,且满足 , 则不等式的解集是( )A、 B、 C、 D、
6. 已知曲线 在点 处的切线方程为 ,则( )A、 B、 C、 D、7. 埃及金字塔之谜是人类史上最大的谜,它的神奇远远超过了人类的想象.在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,142857×4=571428,...,所以这组数字又叫“走马灯数”.该组数字还有如下发现:142+857=999,428+571=999,285+714=999,...,若从这组神秘数字中任选3个数字构成一个三位数 ,剩下的三个数字构成另一个三位数 ,若 ,则所有可能的有序实数组 的个数为( )A、48 B、60 C、96 D、1208. 已知的定义域为 , 为的导函数,且满足 , 则不等式的解集是( )A、 B、 C、 D、二、多选题
-
9. 设 , 则下列结论正确的是( )A、 B、 C、 D、10. 已知 为自然对数的底数,则下列不等式一定成立的是( )A、 B、 C、 D、11. 中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设为整数,若和被除得的余数相同,则称和对模同余,记为 . 若 , , 则的值可以是( )A、2005 B、2006 C、2020 D、202112. 某数学研究小组在研究牛顿三叉戟曲线时通过数学软件绘制出其图象(如图),并给出以下几个结论,则正确的有( )
 A、函数的极值点有且只有一个 B、当时,恒成立 C、过原点且与曲线相切的直线有且仅有2条 D、若 , 则的最小值为
A、函数的极值点有且只有一个 B、当时,恒成立 C、过原点且与曲线相切的直线有且仅有2条 D、若 , 则的最小值为三、填空题
-
13. 在的展开式中,的系数是.14. 杨辉三角在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中被记载.它的开头几行如图所示,它包含了很多有趣的组合数性质,如果将杨辉三角从第1行开始的每一个数都换成分数 , 得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,请问“莱布尼茨三角形”第9行第4个数是 .
杨辉三角
莱布尼茨三角形
第0行第1行
第2行
第3行
第n行
11 1
1 2 1
1 3 3 1
1 … 1
1
第0行
第1行
第2行
第3行
15. 党的十九大报告提出“乡村振兴战略”,要“推动城乡义务教育一体化发展,高度重视农村义务教育”.为了响应报告精神,某师范大学5名毕业生主动申请到某贫困山区的乡村小学工作、若将这5名毕业生分配到该山区的3所乡村小学,每所学校至少分配1人,则分配方案的总数为.16. 函数 , 当时,零点的个数是;若存在实数 , 使得对于任意 , 都有 , 则实数的取值范围是.四、解答题
-
17. 在下列三个条件中任选一个条件,补充在问题中的横线上,并解答.
条件①:展开式中前三项的二项式系数之和为22;条件②:展开式中所有项的二项式系数之和减去展开式中所有项的系数之和等于64;条件③:展开式中常数项为第三项.
问题:已知二项式 , 若____,求:
(1)、展开式中二项式系数最大的项;(2)、展开式中所有的有理项.18. 某学习小组有3个男生和4个女生共7人:(1)、将此7人排成一排,男女彼此相间的排法有多少种?(2)、将此7人排成一排,男生甲不站最左边,男生乙不站最右边的排法有多少种?(3)、从中选出2名男生和2名女生分别承担4种不同的任务,有多少种选派方法?(4)、现有7个座位连成一排,仅安排4个女生就座,恰有两个空位相邻的不同坐法共有多少种?19. 已知函数 , 是的一个极值点.(1)、求b的值;(2)、当时,求函数的最大值.