江苏省连云港市灌南县2021-2022学年高二下学期数学期中试卷
试卷更新日期:2023-03-24 类型:期中考试
一、单选题
-
1. 已知 , 则x可能取值为( )A、6 B、7 C、8 D、92. 在正方体中, , 则( )A、 B、 C、 D、3. 已知向量 , , 若 , 则( )A、1 B、 C、 D、24. 已知随机变量服从正态分布 , 且 , 则( )A、0.2 B、0.3 C、0.4 D、0.65. 一个频数分布表(样本容量为30)不小心被损坏了一部分,若样本中数据在[20,60)内的频率为0.8,则样本中在[40,60)内的数据个数为( )
 A、15 B、16 C、17 D、196. 下列说法正确的有( )A、设随机变量X服从二项分布 , 则 B、若X是随机变量,则E(2X+1)=2E(X)+1,D(2X+1)=4D(X)+1 C、已知随机变量ξ~N(0,1),若P(ξ>1)=p,则P(ξ>-1)=1-2p D、设随机变量ξ表示发生概率为p的事件在一次随机实验中发生的次数,7. 如图所示,A,B两点共有5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为 , 则的值为( )
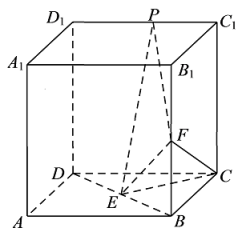
A、15 B、16 C、17 D、196. 下列说法正确的有( )A、设随机变量X服从二项分布 , 则 B、若X是随机变量,则E(2X+1)=2E(X)+1,D(2X+1)=4D(X)+1 C、已知随机变量ξ~N(0,1),若P(ξ>1)=p,则P(ξ>-1)=1-2p D、设随机变量ξ表示发生概率为p的事件在一次随机实验中发生的次数,7. 如图所示,A,B两点共有5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为 , 则的值为( ) A、 B、 C、 D、8. 在长方体中, , , 是线段上的一动点,如下的四个命题中,
A、 B、 C、 D、8. 在长方体中, , , 是线段上的一动点,如下的四个命题中,
(1)平面;(2)与平面所成角的正切值的最大值是;
(3)的最小值;(4)以为球心,为半径的球面与侧面的交线长是 .真命题共有几个( )
A、1 B、2 C、3 D、4二、多选题
-
9. 对于m∈N*,n∈N*,m≤n,关于下列排列组合数,结论正确的是( )A、 B、 C、 D、10. 已知的二项展开式中二项式系数之和为64,则下列结论正确的是( )A、二项展开式中无常数项 B、二项展开式中第3项为 C、二项展开式中各项系数之和为 D、二项展开式中二项式系数最大的项为11. 已知空间中三点A(0,1,0),B(1,2,0),C(-1,3,1),则正确的有( )A、与是共线向量 B、平面ABC的一个法向量是(1,-1,3) C、与夹角的余弦值是 D、与方向相同的单位向量是(1,1,0)12. 现有一款闯关游戏,共有关,规则如下:在第关要抛掷骰子次,每次观察向上面的点数并做记录,如果这次抛掷所出现的点数之和大于 , 则算闯过第关,.假定每次闯关互不影响,则( )A、直接挑战第关并过关的概率为 B、连续挑战前两关并过关的概率为 C、若直接挑战第关,设 “三个点数之和等于”, “至少出现一个点”,则 D、若直接挑战第关,则过关的概率是
三、填空题
-
13. 求值: .14. 2022年北京冬奥会即将开幕,某校4名学生报名担任志愿者.将这4名志愿者分配到3个比赛场馆,每个比赛场馆至少分配一名志愿者,则所有分配方案共有种.(用数字作答)15. 已知空间向量 , 且 , 则n= , 向量与的夹角为 .16. 如图所示,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10,…,记这个数列的前n项和为S(n),则S(16)的值为.

四、解答题
-
17. 在二项式的展开式中,求:(1)、二项式系数之和;(2)、各项系数之和;18. 一组学生共有7人.(1)、若有3名男生、4名女生,全体排成一排,男生互不相邻,求不同的排列方法总数;(2)、全体排成一排,甲既不站排头也不站接尾,求不同的排列方法总数;(3)、如果从中选出男生2人,女生2人,参加三项不同的活动,要求每人参加一项且每项活动都有人参加的选法有648种,问该组学生中男、女生各有多少人?19. 甲袋中有3个白球和2个红球,乙袋中有2个白球和3个红球,丙袋中有4个白球和4个红球.先随机取一只袋,再从该袋中先随机取1个球不放回,接着再从该袋中取1个球.(1)、求第一次取出的球为红球的概率;(2)、求第一次取出的球是红球的前提下,第二次取出的球是白球的概率.20. 冬奥会的全称是冬季奥林匹克运动会,是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会于2022年在中国北京和张家口举行.为了弘扬奥林匹克精神,让学生了解更多的冬奥会知识,某学校举办了有关2022年北京冬奥会知识的宣传活动,其中有一项为抽卡答题活动,盒中装有9张大小相同的精美卡片,卡片上分别印有北京冬奥会的吉祥物“冰墩墩”和“雪容融”.卡片背面都有关于冬奥会的问题,答对则奖励与卡片对应的吉祥物玩偶.其中“冰墩墩”卡片有5张,编号分别为1,2,3,4,5;“雪容融”卡片有4张,编号分别为1,2,3,4,从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同).
 (1)、求取出的4张卡片中,含有编号为4的卡片的概率;(2)、在取出的4张卡片中,“冰墩墩”卡片的个数设为X.求随机变量X的分布列.
(1)、求取出的4张卡片中,含有编号为4的卡片的概率;(2)、在取出的4张卡片中,“冰墩墩”卡片的个数设为X.求随机变量X的分布列.