吉林省通化市2021-2022学年高二下学期数学期中试卷

试卷更新日期：2023-03-24 类型：期中考试

进入出卷网下载

一、单选题

1. 二项式 ${(a + b)}^{6}$ 的展开式中共有（）项.

A、5 B、6 C、7 D、8

查看试题解析
2. 已知 $ξ \sim N (0, σ^{2})$ ，且 $P (- 2 \leq ξ \leq 0) = 0.4$ ，则 $P (ξ > 2)$ 等于（）

A、0.1 B、0.2 C、0.6 D、0.8

查看试题解析
3. 习近平总书记在“十九大”报告中指出：坚定文化自信，推动中华优秀传统文化创造性转化．“杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律，最早在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现，欧洲数学家帕斯卡在1654年才发现这一规律，比杨辉要晚近四百年．“杨辉三角”是中国数学史上的一个伟大成就，激发起一批又一批数学爱好者的探究欲望．如图所示，在由二项式系数所构成的“杨辉三角”中，第10行第9个数是（）

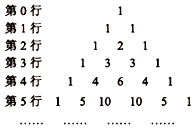A、9 B、10 C、36 D、45

查看试题解析
4. 设i为虚数单位，则(1＋i)⁶展开式中的第三项为（）

A、－20i B、15i C、20 D、－15

查看试题解析
5. 已知某一随机变量ξ的概率分布列如图所示，且E(ξ)＝6.3，则a的值为（）

ξ

4

a

9

P

0.5

0.1

b

A、5 B、6 C、7 D、8

查看试题解析
6. 某班有6名班干部，其中4名男生，2名女生.从中选出3人参加学校组织的社会实践活动，在男生甲被选中的情况下，女生乙也被选中的概率为（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 已知η的分布列为
η
－1
0
1
P
$\frac{1}{2}$
$\frac{1}{3}$
$\frac{1}{6}$
设ξ＝3η－2，则D(ξ)的值为（）

A、5 B、 $\frac{5}{3}$ C、 $\frac{5}{9}$ D、－3

查看试题解析
8. 袋中有大小相同的5个球，分别标有1，2，3，4，5五个号码，现在在有放回抽取的条件下依次取出两个球，设两个球的号码之和为随机变量X，则X所有可能取值的个数是（）

A、5 B、9 C、10 D、25

查看试题解析
9. 志愿服务是办好2022年北京冬奥会的重要基础和保障，冬奥会城市志愿者已于2021年12月5日在主要服务站点开始上岗，预计2022年1月25日开始全面上岗服务．现有4名志愿者要安排到3个服务站点参加服务，每名志愿者只能安排到一个站点，每个站点至少安排一名志愿者，则不同的安排方案共有（）

A、48种 B、36种 C、24种 D、12种

查看试题解析
10. 小芳用人体语言把成语的意思传递给本组其他同学.若小组内同学甲猜对成语的概率是 $0.4$ ，同学乙猜对成语的概率是 $0.5$ ，且规定猜对得 $1$ 分，猜不对得 $0$ 分，则这两个同学各猜1次，得分之和 $X$ （单位：分）的均值为（）

A、0.9 B、0.8 C、1.2 D、1.1

查看试题解析

二、填空题

11. 二项式 ${(x^{2} - \frac{1}{x})}^{6}$ 的展开式中，常数项的值是.

查看试题解析
12. 4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名同学，则不同的安排方法共有种.

查看试题解析
13. 已知随机变量X的分布列为 $P (X = k) = \frac{1}{3}$ ， k=3，6，9，则D(X)等于.

查看试题解析
14. 设随机变量 $X$ 的分布列为 $P (X = k) = m {(\frac{2}{3})}^{k}$ ， $k = 1 ， 2 ， 3$ ，则 $m$ 的值为

查看试题解析

三、解答题

15.

(1)、由数字1，2，3，4，5可以组成多少个三位数（各位上的数字可以重复）？

(2)、解方程： $C_{18}^{x} = C_{18}^{3 x - 6}$ ．

查看试题解析
16. 已知在 ${(\frac{1}{2} x^{2} - \frac{1}{\sqrt{x}})}^{n}$ 的展开式中，第9项为常数项.
求：

(1)、展开式中 $x^{5}$ 的系数.

(2)、 $n$ 的值；

查看试题解析
17. 3名男生，4名女生，按照不同的要求排队，求不同的排队方案的方法种数．

(1)、选其中5人排成一排；

(2)、排成前后两排，前排3人，后排4人；

(3)、全体站成一排，男、女各站在一起；

(4)、全体站成一排，男生不能站在一起．

查看试题解析
18. 在某地举办的射击比赛中，规定每位射手射击10次，每次一发．记分的规则为：击中目标一次得3分；未击中目标得0分；并且凡参赛的射手一律另加2分．已知射手小李击中目标的概率为0.8，求小李在比赛中得分的数学期望与方差．

查看试题解析
19. 某市教育部门规定，高中学生三年在校期间必须参加不少于80小时的社区服务．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段 $[75 ， 80)$ ， $[80 ， 85)$ ， $[85 ， 90)$ ， $[90 ， 95)$ ， $[95 ， 100]$ （单位：小时）进行统计，其频率分布直方图如图所示．

(1)、求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；

(2)、从全市高中学生（人数很多）中任意选取3位学生，记 $X$ 为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量 $X$ 的分布列和数学期望 $E X$ ．

查看试题解析

ξ	4	a	9
P	0.5	0.1	b

η	－1	0	1
P	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{6}$