2023学年安徽省中考数学优质仿真一模卷（一)

试卷更新日期：2023-03-24 类型：中考模拟

进入出卷网下载

一、单选题（每题4分，共40分）

1. $- \frac{1}{2023}$ 的倒数是（）

A、2023 B、 $\frac{1}{2023}$ C、 $- 2023$ D、 $- \frac{1}{2022}$

查看试题解析
2. 长江干流上的葛洲坝、三峡向家坝、溪洛渡、白鹤滩、乌东德6座巨型梯级水电站，共同构成目前世界上最大的清洁能源走廊，总装机容量71695000千瓦，将71695000用科学记数法表示为（）

A、 $7.1695 \times 1 0^{7}$ B、 $716.95 \times 1 0^{5}$ C、 $7.1695 \times 1 0^{6}$ D、 $71.695 \times 1 0^{6}$

查看试题解析
3. 下列运算正确的是（）

A、 ${(- a^{2})}^{3} = - a^{5}$ B、 $a^{3} \cdot a^{5} = a^{15}$ C、 ${(- a^{2} b^{3})}^{2} = a^{4} b^{6}$ D、 $3 a^{2} - 2 a^{2} = a$

查看试题解析
4. 如图所示，该几何体的主视图是（）

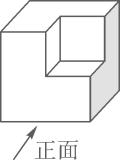A、 B、 C、 D、

查看试题解析
5. 如图，直线 $A B ∥ C D ， A B$ 平分 $∠ E A D ， ∠ 2 = 35 °$ ，则 $∠ 1$ 的度数是（）

A、 $90 °$ B、 $100 °$ C、 $110 °$ D、 $105 °$

查看试题解析
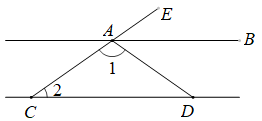6. 如图，一个宽为 $2 c m$ 的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“ $2$ ”和“ $8$ ”（单位： $c m$ ），那么该圆的半径为（）

A、 $\sqrt{13} c m$ B、 $\frac{25}{16} c m$ C、 $3 c m$ D、 $\frac{13}{4} c m$

查看试题解析
7. 因疫情防控需要，一辆货车先从甲地出发运送防疫物资到乙地，稍后一辆轿车从甲地急送防疫专家到乙地．已知甲、乙两地的路程是 $330 k m$ ，货车行驶时的速度是 $60 k m / h$ ．两车离甲地的路程 $s (k m)$ 与时间 $t (h)$ 的函数图象如图所示．下列结论：① $a = 1.5$ ②轿车追上货车时，轿车离甲地 $150 k m$ ③轿车的速度为 $100 k m / h$ ④轿车比货车早 $0.7 h$ 时间到达乙地．其中正确的是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
8. 某小组作“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能的是（）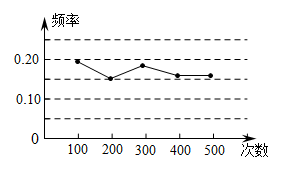

A、掷一个质地均匀的正六面体骰子，向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 C、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” D、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球

查看试题解析
9. 如图，抛物线y＝﹣2x²+8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C₁ ，将C₁向右平移得C₂ ， C₂与x轴交于点B，D．若直线y＝x+n与C₁、C₂共有3个不同的交点，则n的取值范围是（）

A、 $- 2$ ＜n＜ $\frac{1}{8}$ B、 $- 3$ ＜n＜ $- \frac{7}{4}$ C、 $- 3$ ＜n＜ $- 2$ D、 $- 3$ ＜n＜ $- \frac{15}{8}$

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $A B = 3 \sqrt{3}$ ， $A D = 3$ ， $∠ A = 60 ° .$ 点 $E$ 在 $A B$ 边上，将 $△ A D E$ 沿着直线 $D E$ 翻折得 $△ A' D E .$ 连结 $A' C$ ，若点 $A'$ 恰好落在 $∠ B C D$ 的平分线上，则 $A'$ ， $C$ 两点间的距离为（）

A、3或6 B、3或 $\frac{3 \sqrt{3}}{2}$ C、 $\frac{3 \sqrt{3}}{2}$ D、6

查看试题解析

二、填空题（每空5分，共20分）

11. 满足不等式 $2 (2 x - 4) > - 3 x + 6$ 的最小整数是．

查看试题解析
12. 若 $x_{1}$ ， $x_{2}$ 是关于x的方程 $x^{2} - 2 x - 5 = 0$ 的两个实数根，则代数式 $x_{1}^{2} - 3 x_{1} - x_{2} + 4$ 的值是.

查看试题解析
13. 如图所示，点 $B (2 ， 0)$ 是x轴正半轴上一点，以 $O B$ 为斜边作等腰 $R t △ A O B$ ，直角顶点A在第一象限.反比例函数 $y = \frac{k}{x} (x > 0)$ 图象交 $A O$ 于点C，交 $A B$ 于D，若 $A C = B D$ ，求 $k =$ .

查看试题解析
14. 已知关于 $x$ 的二次函数 $y = 3 x_{}^{2} - 6 a x + 4 a_{}^{2} + 2 a + 4$ ，其中 $a$ 为实数，当-2≤x≤1时， $y$ 的最小值为4，满足条件的 $a$ 的值为。

查看试题解析

三、解答题（共9题，共90分）

15. 计算 $2 c o s^{2} 4 5^{∘} - \sqrt{{(t a n 6 0^{∘} - 2)}^{2}} - {(s i n 6 0^{∘} - 1)}^{0} + {(\frac{1}{4})}^{- 1}$ .

查看试题解析
16. 《九章算术》记载了一个方程的问题，译为：今有上禾6束，减损其中之“实”十八升，与下禾10束之“实”相当；下禾15束，减损其中之“实”五升，与上禾5束之“实”相当．问上、下禾每束之实各为多少升？

查看试题解析
17.

(1)、计算并观察下列各式：
第1个： $(a - b) (a + b) =$ ；
第2个： $(a - b) (a^{2} + a b + b^{2}) =$ ；
第3个： $(a - b) (a^{3} + a^{2} b + a b^{2} + b^{3}) =$ ；
……
这些等式反映出多项式乘法的某种运算规律．

(2)、猜想：若n为大于1的正整数，则 $(a - b) (a^{n - 1} + a^{n - 2} b + a^{n - 3} b^{2} + ⋯ + a^{2} b^{n - 3} + a b^{n - 2} + b^{n - 1}) =$ ；

(3)、利用（2）的猜想计算： $2^{n - 1} + 2^{n - 2} + 2^{n - 3} + ⋯ + 2^{3} + 2 + 1 =$ ．

(4)、拓广与应用： $3^{n - 1} + 3^{n - 2} + 3^{n - 3} + ⋯ + 3^{3} + 3 + 1 =$ ．

查看试题解析
18. 如图，在 $8 \times 11$ 网格图中， $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 是位似图形．

（ 1 ）若在网格上建立平面直角坐标系，使得点A的坐标为 $(- 1 ， 6)$ ，点 $C_{1}$ 的坐标为 $(2 ， 3)$ ，写出点B的坐标；

（ 2 ）以点A为位似中心，在网格图中作 $△ A B_{2} C_{2}$ ，使 $△ A B_{2} C_{2}$ 和 $△ A B C$ 位似，且位似比为1：2；

（ 3 ）在图上标出 $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 的位似中心P ，并写出点P的坐标．

查看试题解析
19. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $A D$ 是 $⊙ O$ 的直径， $F$ 是 $A D$ 延长线上一点，连接 $C D ， C F$ ，且 $∠ D C F = ∠ C A D$ .

(1)、求证： $C F$ 是 $⊙ O$ 的切线；

(2)、若直径 $A D = 10 ， c o s B = \frac{3}{5}$ ，求 $F D$ 的长.

查看试题解析
20. 如图所示，九（1）班数学兴趣小组为了测量河对岸的古树A、B之间的距离，他们在河边与AB平行的直线l上取相距60m的C、D两点，测得∠ACB＝15°，∠BCD＝120°，∠ADC＝30°.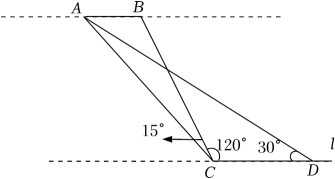

(1)、求河的宽度；

(2)、求古树A、B之间的距离.（结果保留根号）

查看试题解析
21. 成都市某旅游机构抽样调查了外地游客对A、B、C、D四个景点作为最佳旅游景点的喜爱情况，并将调查情况绘制成如图两幅不完整统计图：

(1)、本次参加抽样调查的游客有 ▲ 人，根据题中信息补全条形统计图.

(2)、若某批次游客有6000人，请你估计选择D作为最佳旅游景点的有人.

(3)、A旅游景点举行游客有奖问答活动.现有2男2女4名游客回答对了问题.现从4名游客中随机抽取2名游客发放纪念品，请用列表或画树状图的方法求获得此次纪念品的是一男一女的概率.

查看试题解析
22. 如图，在矩形ABCD中，E为CD的中点，F为BE上的一点，连结CF并延长交AB于点M，MN⊥CM交射线AD于点N.

(1)、当F为BE中点时，求证：AM＝CE；

(2)、若 $\frac{A B}{B C} = \frac{E F}{B F} = 2$ ，求 $\frac{A N}{N D}$ 的值.

查看试题解析
23. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $O B A$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $O A = 8 m$ ，桥拱顶点 $B$ 到水面的距离是 $4m$ .

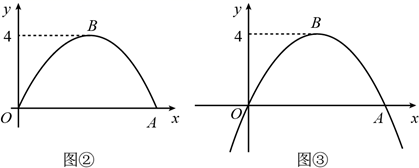(1)、按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

(2)、一只宽为 $1 .2m$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $O$ 点 $0 .4m$ 时，桥下水位刚好在 $O A$ 处.有一名身高 $1.68 m$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

(3)、如图③，桥拱所在的函数图象是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，该抛物线在 $x$ 轴下方部分与桥拱 $O B A$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $m (m > 0)$ 个单位长度，平移后的函数图象在 $8 \leq x \leq 9$ 时， $y$ 的值随 $x$ 值的增大而减小，结合函数图象，求 $m$ 的取值范围.

查看试题解析