初中七年级下学期数学期末测试卷（一）

试卷更新日期：2023-03-24 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在测量跳远成绩的示意图中，直线 $l$ 是起跳线，则需要测量的线段是（）

A、 $A B$ B、 $A C$ C、 $D C$ D、 $B C$

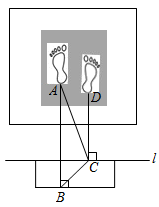查看试题解析
2. 已知三条射线OA，OB，OC，OA⊥OC，∠AOB＝60°，则∠BOC等于（）

A、150° B、30° C、40°或140° D、30°或150°

查看试题解析
3. 下列等式正确的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $\sqrt{144} = \pm 12$ C、 $\sqrt[3]{- 8} = 2$ D、 $- \sqrt{25} = - 5$

查看试题解析
4. 已知平面直角坐标系中，O为坐标原点，点 $A (- 5 ， 4)$ ， $B (x ， y)$ ，将线段A $B$ 平移，使A与O重合，此时B点的对应点 $B^{'}$ 坐标为（2，-1），则 $B$ 点的坐标是（）

A、 $(7 ， - 5)$ B、 $(3 ， - 3)$ C、 $(- 3 ， 3)$ D、 $(- 7 ， 5)$

查看试题解析
5. 下列说法错误的是（）

A、x轴上的点的纵坐标为0 B、点 $P (- 1 ， 3)$ 到y轴的距离是1 C、若点 $A (- a - 1 ， 2)$ 在第二象限，那么 $a > - 1$ D、若 $x y < 0$ ，那么点 $Q (x ， y)$ 在第四象限

查看试题解析
6. 如图，已知 $A_{1} (1 ， 0) ， A_{2} (1 ， - 1) ， A_{3} (- 1 ， - 1) ， A_{4} (- 1 ， 1) ， A_{5} (2 ， 1)$ ，则点 $A_{2020}$ 的坐标是（）

A、 $(506 ， 505)$ B、 $(- 506 ， 507)$ C、 $(- 506 ， 506)$ D、 $(- 505 ， 505)$

查看试题解析
7. 已知实数x，y，z满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式3(x﹣z)+1的值是（）

A、﹣2 B、﹣4 C、﹣5 D、﹣6

查看试题解析
8. 在方程组 ${\begin{array}{l} 2 x + y = 1 - m \\ x + 2 y = 2 \end{array}$ 中，若未知数 $x$ 、 $y$ 满足 $x + y > 0$ ，则 $m$ 的取值范围应为（）

A、 $m < 3$ B、 $m > 3$ C、 $m < 0$ D、 $m > 0$

查看试题解析
9. 某玩具厂共有300名生产工人，每个工人每天可生产玩具车架20个或车轮40个，且1个车架与4个车轮可配成一套，设有x个工人生产车架，y个工人生产车轮，下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 300 \\ 40 x = 20 y \end{array}$ B、 ${\begin{array}{l} x + y = 300 \\ 20 x = 40 y \end{array}$ C、 ${\begin{array}{l} x + y = 300 \\ 4 \times 20 x = 40 y \end{array}$ D、 ${\begin{array}{l} x + y = 300 \\ 20 x = 4 \times 40 y \end{array}$

查看试题解析
10. 为了解某地区七年级10000名学生的体重情况，现从中抽测了500名学生的体重，就这个问题来说，下面的说法中正确的是（）

A、10000名学生是总体 B、每个学生是个体 C、500名学生是所抽取的一个样本 D、样本容量是500

查看试题解析

二、填空题

11. 如图，直线AB、CD相交于点O，OE平分 $∠ B O D$ ， OF平分 $∠ C O E$ ．若 $∠ A O C = 76 °$ ，则 $∠ B O F$ 的度数为°．

查看试题解析
12. 若 $∠ 1$ 与 $∠ 2$ 是对顶角， $∠ 3$ 与 $∠ 2$ 互余，且 $∠ 3 = 3 7^{∘}$ ，则 $∠ 1$ 的度数为°.

查看试题解析
13. 8的立方根为x，4是 $y + 1$ 的一个平方根，则 $x - y =$ ．

查看试题解析
14. $\sqrt[3]{\frac{1}{64}}$ 的立方根是．

查看试题解析
15. 已知点 $M (2 a + b + 1 ， a - 2 b)$ 在x轴正半轴上，则a的取值范围是．

查看试题解析
16. 已知点 $P (x ， y)$ 的坐标满足 $| x | = 3$ ， $\sqrt{y} = 2$ ，且 $x y < 0$ ，则点 $P$ 的坐标是

查看试题解析
17. 若方程 $x^{2 a - b} - 3 y^{a + b} = 2$ 是关于x、y的二元一次方程，则 $a b =$ ．

查看试题解析
18. 已知关于a，b的方程组 ${\begin{array}{l} 3 a + 2 b = 4 \\ 2 a + 3 b = 5 \end{array}$ ，则a﹣b的值为．

查看试题解析
19. 运行程序如图所示，规定：从“输入一个值x”到“结果是否＞5”为一次程序操作，如果程序操作进行了两次才停止，那么x的取值范围是．

查看试题解析
20. 为了鼓励学生课外阅读，学校公布了“阅读奖励”方案，征求了所有学生的意见，赞成、反对、无所谓三种意见的人数之比为7：2：1，画成扇形统计图后，“赞成”所在扇形的圆心角的度数为°．

查看试题解析

三、计算题

21.

(1)、计算： $\sqrt{16} + \sqrt[3]{- 64} - \sqrt{(- 3)^{2}} + | 1 - \sqrt{3} |$

(2)、解不等式： $\frac{1 + x}{2}$ ﹣ $\frac{2 x + 1}{3}$ ≤1；

(3)、解方程组： ${\begin{array}{l} x - 3 y = - 2 ① \\ 2 x + y = 3 ② \end{array}$

查看试题解析

四、解答题

22. 如图，已知AB∥CD ， CF为∠ACD的平分线，∠A＝110°，∠EFC＝35°．
求证：EF∥CD ．

请将下面的证明过程补充完整．

证明：∵AB∥CD ， (已知)

∴∠_▲_＋∠ACD＝180°．（）

∵∠A＝110°，（已知）

∴∠ACD＝_▲_°．(等量代换)

∵CF为∠ACD的平分线，(已知)

∴∠FCD＝ $\frac{1}{2}$ ∠_▲_＝35°．(角平分线定义)

∵∠EFC＝35°，(已知)

∴∠FCD＝∠EFC ， (等量代换)

∴EF∥CD ．（）

查看试题解析
23. 如图所示，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0)，且a，b满足|a+2|+ $\sqrt{b - 4}$ =0，点C的坐标为(0，3)。

(1)、求a，b的值及S_三角形ABC；

(2)、若点Ｍ在x轴上，且S_三角形ACM= $\frac{1}{3}$ S_三角形ABC ，试求点Ｍ的坐标。

查看试题解析
24. 阅读下列材料，然后解答后面的问题.
已知方程组 ${\begin{array}{l} 3 x + 7 y + z = 20 \\ 4 x + 10 y + z = 27 \end{array}$ ，求x+y+z的值.

解：将原方程组整理得 ${\begin{array}{l} 2 (x + 3 y) + (x + y + z) = 20 ① \\ 3 (x + 3 y) + (x + y + z) = 27 ② \end{array}$ ，

②–①，得x+3y=7③，

把③代入①得，x+y+z=6.

仿照上述解法，已知方程组 ${\begin{array}{l} 6 x + 4 y = 22 \\ - x - 6 y + 4 z = - 1 \end{array}$ ，试求x+2y–z的值.

查看试题解析

五、综合题

25. 如图， $M N ∥ A B$ ，点O是 $M N$ 上一点，直线 $E B ， A C$ 经过点O，且 $E B$ 平分 $∠ M O C$ ，过点A作 $A D ⊥ A C$ 于点A，且 $∠ C O N = 40 °$ ；

(1)、求 $∠ B A D$ 的度数；

(2)、连接 $B D$ ，若 $B D ⊥ A D$ ，求 $∠ D B F$ 的度数．

查看试题解析
26. 2022年是富川县大力发展香芋种植的一年，某香芋种植大户聘请了一些临时工帮种植一批香芋，每个工人每天可以种植一亩香芋，计划9天种完，种植3天后由于气象台预测几天后将会有暴雨，为使香芋的种植不受到暴雨的影响，所以该种植大户又聘请了5个工人一起种植香芋，恰好提前两天完成了种植任务．

(1)、问该香芋种植大户种植了多少亩香芋？第一批请了多少个工人帮种植香芋？

(2)、种植过程中每天中午都要给每个工人提供一份快餐，已知烧鹅饭每个21元，排骨蒸饭每个18元，在种植的最后一天，该种植大户计划帮工人们订快餐的总花费不超过300元，则最多能订多少个烧鹅饭？

查看试题解析
27. 随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小李为了了解他的好友的运动情况，随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别： $A$ （0~5000步）（说明：“0~5000”表示大于等于0，小于等于5000，下同）， $B$ （5001~10000步）， $C$ （10001~15000步）， $D$ （15000步以上），统计结果如图所示：
请依据统计结果回答下列问题：

(1)、本次调查中，一共调查了位好友；

(2)、已知 $A$ 类好友人数是 $D$ 类好友人数的5倍．
①请计算 $A$ 和 $D$ 类好友人数，并补全条形图；
②扇形图中，“ $A$ ”对应扇形的圆心角为 ▲ 度；
③若小李微信朋友圈共有好友150人，请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步？

查看试题解析