2023年中考数学复习考点一遍过——图形的相似
试卷更新日期:2023-03-23 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,点D在的边上,添加一个条件,使得 , 下列错误的是( )
 A、 B、 C、 D、2. 如图,在中,D、E分别是边、上的点,且 , , .则下列说法不正确的是( )
A、 B、 C、 D、2. 如图,在中,D、E分别是边、上的点,且 , , .则下列说法不正确的是( ) A、 B、 C、 D、3. 如图,已知 , , , 则的长为( )
A、 B、 C、 D、3. 如图,已知 , , , 则的长为( )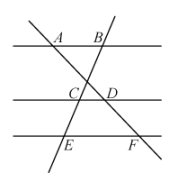 A、2 B、4 C、9 D、104. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( )
A、2 B、4 C、9 D、104. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( ) A、8 B、12 C、16 D、205. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )
A、8 B、12 C、16 D、205. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )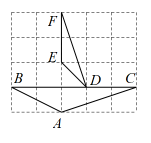 A、 B、 C、 D、6. 两个三角形相似比是3:4,其中小三角形的周长为9,则另一个大三角形的周长是( )A、12 B、16 C、27 D、367. 已知在△ABC中,AB=6,AC=9,D,E分别是AB,AC边上的点,且AD=2. 若△ABC和△ADE相似,则AE=( )A、5 B、3 C、 D、3或8. 如图,若 , , 与交于点 , 且 , , 则等于( )
A、 B、 C、 D、6. 两个三角形相似比是3:4,其中小三角形的周长为9,则另一个大三角形的周长是( )A、12 B、16 C、27 D、367. 已知在△ABC中,AB=6,AC=9,D,E分别是AB,AC边上的点,且AD=2. 若△ABC和△ADE相似,则AE=( )A、5 B、3 C、 D、3或8. 如图,若 , , 与交于点 , 且 , , 则等于( )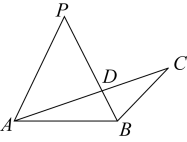 A、3 B、6 C、7 D、129. 如图,在△ABC中,AC=6,BC=8,∠C=90°,∠ABC与∠BAC的平分线交于点D,过点D作DE∥AC交AB于点E,则DE=( )
A、3 B、6 C、7 D、129. 如图,在△ABC中,AC=6,BC=8,∠C=90°,∠ABC与∠BAC的平分线交于点D,过点D作DE∥AC交AB于点E,则DE=( ) A、 B、2 C、 D、310. 如图,边长为5的大正方形是由四个全等的直角三角形和一个小正方形组成,连结并延长交于点M.若 , 则的长为( )
A、 B、2 C、 D、310. 如图,边长为5的大正方形是由四个全等的直角三角形和一个小正方形组成,连结并延长交于点M.若 , 则的长为( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题(每空3分,共27分)
-
11. 如图, , , , 则.
 12. 如图,在▱中,的平分线交于点 , 交于点 , 若 , 则.
12. 如图,在▱中,的平分线交于点 , 交于点 , 若 , 则. 13. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.
13. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.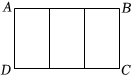 14. 如图,在中,为边上的中线,点G为的重心.若 , 则的长为.
14. 如图,在中,为边上的中线,点G为的重心.若 , 则的长为. 15. 如图,在△ABC中,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则AF:FD= , S△BFD:S△ABC=.
15. 如图,在△ABC中,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则AF:FD= , S△BFD:S△ABC=. 16. 如图,将一张矩形纸片沿折叠,得到两个全等的小矩形.如果矩形矩形 , 那么的值是.
16. 如图,将一张矩形纸片沿折叠,得到两个全等的小矩形.如果矩形矩形 , 那么的值是. 17. 如图,在矩形中, , , E为的中点,G为的中点,F为上的一个动点,当时,的长为.
17. 如图,在矩形中, , , E为的中点,G为的中点,F为上的一个动点,当时,的长为. 18. 如图,菱形中, , 对角线 , E为上一点且 , 连接交于点F,过点F作于点G,则的长度为.
18. 如图,菱形中, , 对角线 , E为上一点且 , 连接交于点F,过点F作于点G,则的长度为.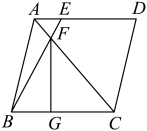
三、综合题(共6题,共63分)
-
19. 如图,已知中, , , 点D、E在边上,.
 (1)、求证:;(2)、当 , 时,求的长.20. 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)、求证:;(2)、当 , 时,求的长.20. 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E. (1)、试说明△ADE∽△PAB;(2)、若PA=x,DE=y,请写出y与x之间的函数关系式.21. 如图,在△ABC中,点D在BC边上,点E在AC边上,且AD=AB,∠DEC=∠B.
(1)、试说明△ADE∽△PAB;(2)、若PA=x,DE=y,请写出y与x之间的函数关系式.21. 如图,在△ABC中,点D在BC边上,点E在AC边上,且AD=AB,∠DEC=∠B. (1)、求证:△AED∽△ADC;(2)、若AE=1,EC=3,求AB的长.22. 如图,E是矩形中边上一点,将沿折叠得到 , 点F落在上.
(1)、求证:△AED∽△ADC;(2)、若AE=1,EC=3,求AB的长.22. 如图,E是矩形中边上一点,将沿折叠得到 , 点F落在上. (1)、求证:;(2)、若 , 求的值;(3)、在中, , , 动点M从点B出发,在边上以每秒的速度向点F匀速运动,同时动点N从点A出发,在边上以每秒的速度向点B匀速运动.设运动时间为 , 连接 , 若与以点B,N,M为顶点的三角形相似,求t的值.23. 我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
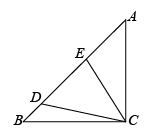
(1)、求证:;(2)、若 , 求的值;(3)、在中, , , 动点M从点B出发,在边上以每秒的速度向点F匀速运动,同时动点N从点A出发,在边上以每秒的速度向点B匀速运动.设运动时间为 , 连接 , 若与以点B,N,M为顶点的三角形相似,求t的值.23. 我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.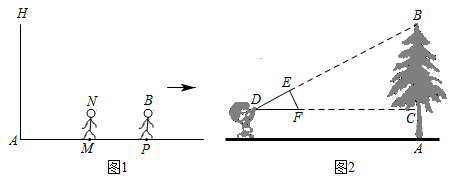 (1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.24.(1)、【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:;
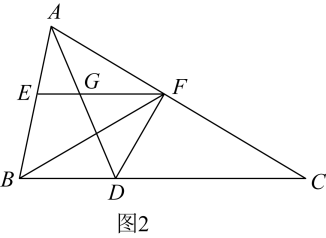
(1)、请在图中画出路灯O和影子端点Q的位置.(2)、估计路灯的高,并求影长的步数.(3)、无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度 , 他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得 , , , 小明眼睛到地面的距离为 , 则树高为m.24.(1)、【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:; (2)、【尝试应用】
(2)、【尝试应用】如图2,在(1)的条件下,连结 , , 若 , 、恰好将三等分,求的值;
 (3)、【拓展延伸】
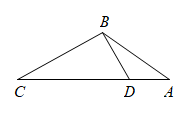
(3)、【拓展延伸】如图3,在等边中, , 连结 , 点E在上,若 , 求的值.