2023年中考数学复习考点一遍过——平移、旋转变换
试卷更新日期:2023-03-23 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 2022年新能源车企迎来了更多的关注,如图是四款新能源汽车的标志,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点A1的坐标为( )A、(-3,5) B、(-3,3) C、(-3,-1) D、(0,2)3. 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
2. 在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点A1的坐标为( )A、(-3,5) B、(-3,3) C、(-3,-1) D、(0,2)3. 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( ) A、90° B、80° C、50° D、30°4. 如图,在平面直角坐标系中,将点A(3,2)绕原点O逆时针旋转90°得到点B,则点B的坐标为( )
A、90° B、80° C、50° D、30°4. 如图,在平面直角坐标系中,将点A(3,2)绕原点O逆时针旋转90°得到点B,则点B的坐标为( ) A、(-2,3) B、(-3,2) C、(-2,-3) D、(-1,3)5. 一个数a在数轴上表示的点是A,当点A在数轴上向左移动了6个单位长度后到点B,点A与点B表示的数恰好互为相反数,则数a是( )A、-3 B、-6 C、6 D、36. 点关于原点的对称点的坐标是( )A、 B、 C、 D、7. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、8. 在图形的旋转过程中,下面有四种说法:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后图形的对应线段相等;④旋转前、后图形的位置一定会改变.上述四种说法正确的有( )A、1个 B、2个 C、3个 D、4个9. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )
A、(-2,3) B、(-3,2) C、(-2,-3) D、(-1,3)5. 一个数a在数轴上表示的点是A,当点A在数轴上向左移动了6个单位长度后到点B,点A与点B表示的数恰好互为相反数,则数a是( )A、-3 B、-6 C、6 D、36. 点关于原点的对称点的坐标是( )A、 B、 C、 D、7. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、8. 在图形的旋转过程中,下面有四种说法:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后图形的对应线段相等;④旋转前、后图形的位置一定会改变.上述四种说法正确的有( )A、1个 B、2个 C、3个 D、4个9. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )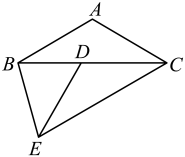 A、30° B、45° C、55° D、75°10. 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
A、30° B、45° C、55° D、75°10. 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( ) A、-2 B、1 C、 D、2
A、-2 B、1 C、 D、2二、填空题(每空3分,共24分)
-
11. 如图,将长5cm,宽3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为 cm2 .
 12. 如图,将绕点A逆时针旋转120°,得到 . 若点D在线段BC的延长线上,则 .
12. 如图,将绕点A逆时针旋转120°,得到 . 若点D在线段BC的延长线上,则 . 13. 将△OAB按如图的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,),将△OAB绕原点O逆时针旋转60°得到点△OA'B′,则点A'的坐标为.
13. 将△OAB按如图的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,),将△OAB绕原点O逆时针旋转60°得到点△OA'B′,则点A'的坐标为. 14. 如图,将绕点O按逆时针方向旋转55°后得到 , 若 , 则的度数是 .
14. 如图,将绕点O按逆时针方向旋转55°后得到 , 若 , 则的度数是 . 15. 如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到的位置, , , 平移距离为6,则阴影部分的面积为 .
15. 如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到的位置, , , 平移距离为6,则阴影部分的面积为 .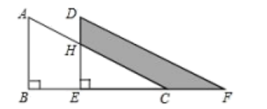 16. 如图,在矩形中, , , 矩形绕点逆时针旋转一定角度得矩形 , 若点的对应点落在边上,则的长为.
16. 如图,在矩形中, , , 矩形绕点逆时针旋转一定角度得矩形 , 若点的对应点落在边上,则的长为. 17. 如图,在矩形中, , .矩形绕点逆时针旋转一定角度得到矩形.若点的对应点落在边上,则的长为.
17. 如图,在矩形中, , .矩形绕点逆时针旋转一定角度得到矩形.若点的对应点落在边上,则的长为. 18. 如图,P是正方形ABCD内一点,且点P到点B、C、D的距离分别为、、4,则的度数为
18. 如图,P是正方形ABCD内一点,且点P到点B、C、D的距离分别为、、4,则的度数为
三、综合题(共6题,共66分)
-
19. 如图,的顶点坐标分别为 , , .将绕原点O逆时针旋转的图形得到.
 (1)、画出的图形;(2)、将点绕原点O逆时针旋转 , 求点旋转后对应点的坐标.(用含m的式子表示)20. 已知:如图,的面积为 , , 现将沿直线向右平移个单位到的位置.
(1)、画出的图形;(2)、将点绕原点O逆时针旋转 , 求点旋转后对应点的坐标.(用含m的式子表示)20. 已知:如图,的面积为 , , 现将沿直线向右平移个单位到的位置. (1)、求中边上的高;(2)、若 ,
(1)、求中边上的高;(2)、若 ,求线段的长;
连接 , 当是等腰三角形时,求的值.
21. 在五边形中,四边形是矩形,是以E为直角顶点的等腰直角三角形.与交于点G,将直线绕点E顺时针旋转交于点F. (1)、求证:;(2)、判断线段 , , 之间的数量关系,并说明理由;(3)、若 , 且 , 求线段的长.22. 在Rt△ABC中,AC=BC,将线段CA绕点C旋转α(0°<α<90°),得到线段CD,连接AD、BD.
(1)、求证:;(2)、判断线段 , , 之间的数量关系,并说明理由;(3)、若 , 且 , 求线段的长.22. 在Rt△ABC中,AC=BC,将线段CA绕点C旋转α(0°<α<90°),得到线段CD,连接AD、BD. (1)、如图1,将线段CA绕点C逆时针旋转α,则∠ADB的度数为 ;(2)、将线段CA绕点C顺时针旋转α时
(1)、如图1,将线段CA绕点C逆时针旋转α,则∠ADB的度数为 ;(2)、将线段CA绕点C顺时针旋转α时①在图2中依题意补全图形,并求∠ADB的度数;
②若∠BCD的平分线CE交BD于点F,交DA的延长线于点E,连结BE.用等式表示线段AD、CE、BE之间的数量关系,并证明.

