2023年中考数学复习考点一遍过——命题与证明

试卷更新日期：2023-03-23 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列语句是命题的是（）

A、作直线AB的垂线 B、在线段AB上取点C C、垂线段最短吗？ D、同旁内角互补

查看试题解析
2. 下列命题中，假命题是（）

A、对顶角相等 B、内错角相等 C、两个全等三角形的面积相等 D、同一平面内，垂直于同一条直线的两条直线平行

查看试题解析
3. 下列命题中，逆命题是真命题的是（）

A、两直线平行，内错角相等 B、若a＝b，那么a²＝b² C、对顶角相等 D、若a＝b，那么|a|＝|b|

查看试题解析
4. 命题：①对顶角相等；②经过直线外一点，有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等．其中假命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 设边长为3的正方形的对角线长为 $a$ ，则下列说法中错误的是（）

A、 $a$ 是无理数 B、 $a$ 可以用数轴上的一个点来表示 C、 $3 < a < 4$ D、 $a$ 是18的算术平方根

查看试题解析
6. 下列说法正确的是（）
① 0是绝对值最小的有理数；②相反数大于本身的数是负数；③一个有理数不是正数就是负数；④两个数比较，绝对值大的反而小

A、①② B、①③ C、①②③ D、①②③④

查看试题解析
7. 下列说法正确的是（）

A、三角形三条高交于三角形内一点 B、一个钝角三角形一定不是等腰三角形，也不是等边三角形 C、有两条边及其中一条边的对角对应相等的两个三角形全等 D、平面上两个全等的图形不一定关于某直线对称

查看试题解析
8. 下列说法正确的是（）

A、有一角和两边对应相等的两个三角形全等 B、三角形的任意两边之和大于第三边 C、线段不是轴对称图形 D、三角形的重心是这个三角形的三条角平分线的交点

查看试题解析
9. 下列说法中，正确的个数为（　　）
⑴在同圆或等圆中，弦相等则所对的弧相等；
⑵优弧一定比劣弧长；
⑶弧相等则所对的圆心角相等；
⑷在同圆或等圆中，圆心角相等则所对的弦相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 下列选项中，能说明命题“若a≤1，则a²≤1”是假命题的反例是（）

A、a=2 B、a=1 C、a=-1 D、a=-2

查看试题解析

二、填空题（每空3分，共30分）

11. 若要举反例来说明命题“如果 $x \neq 0$ ，那么 $x^{2} > x$ ”是假命题，则可取 $x =$ (写出一种即可)．

查看试题解析
12. “同一平面内，若a⊥b，c⊥b，则a∥c”这个命题的条件是，结论是，这个命题是命题．

查看试题解析
13. 命题：“如果a＝b，那么a²＝b²”的逆命题是命题（填“真”或“假”）．

查看试题解析
14. 直角三角形中两锐角互余，这一命题的逆命题是．

查看试题解析
15. 把命题“同位角相等”改写成“如果……那么……”的形式为．

查看试题解析
16. 用反证法证明某一命题的结论“ $a > b$ ”时，应假设.

查看试题解析
17. 用一个a的值说明“若a是实数，则2a一定比a大”是错误的，这个值可以是．

查看试题解析
18. 下列命题：①不相交的直线是平行线；②同位角相等；③如果两个实数的平方相等，那么这两个实数也相等；④对顶角相等．其中真命题的序号是．

查看试题解析

三、综合题（共6题，共60分）

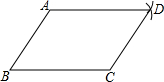
19. 已知命题“如果 $a = b$ ，那么 $| a | = | b |$ ． ”

(1)、写出此命题的条件和结论；

(2)、写出此命题的逆命题；

(3)、判断此命题的逆命题是真命题还是假命题，如果是假命题，请举出一个反例进行说明．

查看试题解析
20. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证．

(1)、在方框中填空，以补全已知和求证；
已知：如图，在四边形ABCD中，

BC＝AD，

AB＝．

求证：四边形ABCD是四边形．

(2)、按嘉淇的想法写出证明：
证明：

(3)、用文字叙述所证命题的逆命题为．

查看试题解析
21. 如图，已知四个关系式：①AC＝DC；②BC＝EC；③∠DCA＝∠ECB：④AB＝DE．

(1)、从上面四个关系式中任取三个为条件，余下的一个为结论，组成一个命题．在组成的命题中真命题的个数是；

(2)、从（1）中选择一个真命题进行证明
已知：

求证：

证明：

查看试题解析
22. 定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”．如图1，在△ABC中，若AB²+AC²-AB⋅AC=BC² ，则△ABC是“和谐三角形”．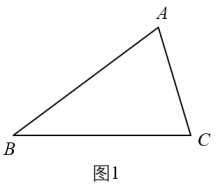

(1)、等边三角形一定是“和谐三角形”，是命题（填“真”或“假”）．

(2)、若Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b>a，若△ABC 是“和谐三角形”，求a：b：c．

查看试题解析
23. 如图，Rt△ABC中，∠ACB＝90°，D、E分别在边AB、AC上，给出下列信息：
①BE平分∠ABC；②CD⊥AB；③∠CFE＝∠CEF.

(1)、请在上述3条信息中选择其中两条作为条件，其余的一条信息作为结论组成一个命题.在保证命题正确的情况下，你选择的条件是，结论是.（只要填写序号）.

(2)、请证明（1）中你组成的命题的正确性.

查看试题解析
24. 探究问题：已知∠ABC ，画一个角∠DEF ，使DE∥AB ， EF∥BC ，且DE交BC于点P ． ∠ABC与∠DEF有怎样的数量关系？

(1)、我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．
①图1中∠ABC与∠DEF数量关系为；图2中∠ABC与∠DEF数量关系为；

请选择其中一种情况说明理由．

②由①得出一个真命题（用文字叙述）：．

(2)、应用②中的真命题，解决以下问题：
若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．

查看试题解析