山东省滨州市阳信县2021-2022学年高一下学期数学期中考试试卷

试卷更新日期：2023-03-23 类型：期中考试

进入出卷网下载

一、单选题

1. 复数 $z$ 满足 $z = - 1 + 2 i$ ，则 $z$ 的虚部为（）

A、 $2 i$ B、 $- 2 i$ C、-1 D、2

查看试题解析
2. 已知 $Δ A B C$ 中， $D$ ， $E$ ， $F$ 分别是 $A B$ ， $A C$ ， $B C$ 的中点，则（）

A、 $\vec{A F} = \frac{3}{2} \vec{A B} + \vec{B E}$ B、 $\vec{A F} = - \frac{3}{2} \vec{A B} + \vec{B E}$ C、 $\vec{A F} = \frac{3}{2} \vec{A B} - \vec{B E}$ D、 $\vec{A F} = - \frac{3}{2} \vec{A B} - \vec{B E}$

查看试题解析

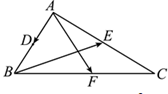3. 袋子中有四张卡片，分别写有“学、习、强、国”四个字，有放回地从中任取一张卡片，将三次抽取后“学”“习”两个字都取到记为事件

A

，用随机模拟的方法估计事件

A

发生的概率，利用电脑随机产生整数0，1，2，3四个随机数，分别代表“学、习、强、国”这四个字，以每三个随机数为一组，表示取卡片三次的结果，经随机模拟产生了以下18组随机数：

232	321	210	023	123	021	132	220	001
231	130	133	231	031	320	122	103	233

由此可以估计事件 $A$ 发生的概率为（）

A、

\frac{2}{9}

B、

\frac{5}{18}

C、

\frac{1}{3}

D、

\frac{7}{18}

查看试题解析

4. 在 $Δ A B C$ 中， $a, b, c$ 分别是角 $A, B, C$ 的对边，满足 $(a + b + c) (a + b - c) = a b$ ，则 $Δ A B C$ 的最大角为（）

A、 $30^{\circ}$ B、 $120^{\circ}$ C、 $90^{\circ}$ D、 $60^{\circ}$

查看试题解析
5. 已知非等向量 $\vec{A B}$ 与 $\vec{A C}$ 满足 $(\frac{\vec{A B}}{| \vec{A B} |} + \frac{\vec{A C}}{| \vec{A C} |}) \cdot \vec{B C} = 0$ ，且 $| \vec{B C} | = \sqrt{3} | \vec{A B} |$ ，则 $△ A B C$ 为（）

A、等腰非等边三角形 B、直角三角形 C、等边三角形 D、三边均不相等的三角形

查看试题解析
6. 走路是“最简单、最优良的锻炼方式”，它不仅可以帮助减肥，还可以增强心肺功能、血管弹性、肌肉力量等.下图为甲、乙两名同学在同一星期内日步数的折线统计图，则下列结论中不正确的是（）

A、这一星期内甲的日步数的中位数为11600 B、这一星期内甲的日步数的平均值大于乙 C、这一星期内甲的日步数的方差大于乙 D、这一星期内乙的日步数的30%分位数是7030

查看试题解析
7. 已知 $△ A B C$ 的外接圆圆心为 $O$ ，且 $2 \vec{A O} = \vec{A B} + \vec{A C} ， | \vec{O A} | = | \vec{A B} |$ ，则向量 $\vec{O C}$ 在向量 $\vec{C A}$ 上的投影向量为（）

A、 $\frac{1}{2} \vec{C A}$ B、 $\frac{\sqrt{3}}{2} \vec{O C}$ C、 $- \frac{1}{2} \vec{C A}$ D、 $- \frac{\sqrt{3}}{2} \vec{O C}$

查看试题解析
8. 已知正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的所有棱长都是2，点M在棱AC上运动，则 $A_{1} M + B M$ 的最小值为（）

A、 $\sqrt{6} + \sqrt{2}$ B、 $\sqrt{3} + 2$ C、 $\frac{\sqrt{6} + \sqrt{2}}{2}$ D、 $\frac{\sqrt{3} + 2}{2}$

查看试题解析

二、多选题

9. 已知复数 $z = \frac{i}{1 - 2 i}$ ，则以下说法正确的是（）

A、 $| z | = \frac{\sqrt{5}}{5}$ B、复数 $z$ 是方程 $5 x^{2} + 4 x + 1 = 0$ 的一个根 C、 $z$ 的共轭复数 $\bar{z} = \frac{2}{5} - \frac{i}{5}$ D、在复平面内与 $z$ 对应的点在第二象限

查看试题解析
10. 下列说法正确的是（）

A、在 $△ A B C$ 中，若 $\vec{A D} = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$ ，则点D是边BC的中点 B、已知 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (x, x - 1)$ ，若 $(\vec{b} - 2 \vec{a}) / / \vec{a}$ ，则 $x = - 1$ C、已知A ， B ， C三点不共线，B ， C ， M三点共线，若 $\vec{A M} = x \vec{A B} + (2 x - 1) \vec{A C}$ ，则 $x = \frac{1}{2}$ D、已知正方形ABCD的边长为1，点M满足 $\vec{D M} = \frac{1}{2} \vec{M C}$ ，则 $\vec{A M} \cdot \vec{A C} = \frac{4}{3}$

查看试题解析
11. 分别抛掷两枚质地均匀的骰子（六个面上的点数分别为1，2，3，4，5，6），设事件 $M =$ “第一枚骰子的点数为奇数”，事件 $N =$ “第二枚骰子的点数为偶数”，则（）

A、M与N互斥 B、 $P (M) = \frac{1}{2}$ C、M与N相互独立 D、 $P (M ∪ N) = \frac{3}{4}$

查看试题解析
12. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别是 $a ， b ， c$ ，下列说法正确的是（）

A、 $A > B$ 是 $s i n A > s i n B$ 的充要条件 B、 $A B = 2 \sqrt{2}$ ， $∠ B = 4 5^{∘}$ ，若 $A C = 3$ ，则这样的三角形有两个 C、若 $\vec{A B} \cdot \vec{B C} < 0$ ，则 $△ A B C$ 为钝角三角形 D、 $△ A B C$ 的面积公式为 $S = \frac{1}{2} a^{2} \frac{s i n B s i n C}{s i n A}$

查看试题解析

三、填空题

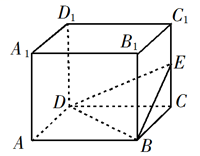
13. 已知向量 $\vec{a} = (1 ， 2) ， \vec{b} = (- 2 ， y)$ ，若 $\vec{a} / / \vec{b}$ ，则 $| 2 \vec{a} - \vec{b} | =$ .

查看试题解析
14. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是120，E为 $C C_{1}$ 的中点，则三棱锥E-BCD的体积是.

查看试题解析
15. 某学校共有教师490人，其中不到40岁的有350人，40岁及以上的有140人，为了了解普通话在该校教师中的推广普及情况，用分层随机抽样的方法，从全体教师中抽取一个容量为70人的样本进行普通话水平测试，其中在不到40岁的教师中应抽取的人数是．

查看试题解析
16. 设 $G$ 为△ $A B C$ 的重心，过点 $G$ 作直线分别交 $A B$ ， $A C$ 于点 $P$ ， $Q$ ，已知 $\vec{A P} = λ \vec{A B}$ ， $\vec{A Q} = μ \vec{A C}$ ，则 $\frac{1}{λ} + \frac{1}{μ} =$ ．

查看试题解析

四、解答题

17. 已知复数 $z$ 使得 $z + 2 i \in R$ ， $\frac{z}{2 - i} \in R$ ，其中 $i$ 是虚数单位.

(1)、求复数 $z$ 的共轭复数 $\bar{z}$ ；

(2)、若复数 ${(z + m i)}^{2}$ 在复平面上对应的点在第四象限，求实数 $m$ 的取值范围.

查看试题解析
18. 已知向量 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (3, - 1)$ .

(1)、若 $(\vec{a} + λ \vec{b}) ⊥ \vec{a}$ ，求实数 $λ$ 的值；

(2)、若 $\vec{c} = 2 \vec{a} - \vec{b}$ ， $\vec{d} = \vec{a} + 2 \vec{b}$ ，求向量 $\vec{c}$ 与 $\vec{d}$ 的夹角.

查看试题解析
19. 在一个如图所示的直角梯形 $A B C D$ 内挖去一个扇形， $E$ 恰好是梯形的下底边的中点，将所得平面图形绕直线 $D E$ 旋转一圈．

(1)、说明所得几何体的结构特征；

(2)、求所得几何体的表面积和体积．

查看试题解析
20. 某中学高一年级举行了一次数学竞赛，从中随机抽取了一批学生的成绩，经统计，这批学生的成绩全部介于50至100之间，将数据按照 $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ 的分组作出频率分布直方图如图所示.

(1)、求频率分布直方图中a的值，并估计本次竞赛成绩的第80百分位数；

(2)、若按照分层随机抽样从成绩在 $[80 ， 90)$ ， $(90 ， 100]$ 的两组中抽取6人，再从这6人中随机抽取2人，求至少有1人的成绩在 $[90 ， 100]$ 内的概率.

查看试题解析
21. 为普及抗疫知识、弘扬抗疫精神，某学校组织防疫知识竞赛.比赛共分为两轮，每位参赛选手均须参加两轮比赛，若其在两轮比赛中均胜出，则视为赢得比赛.已知在第一轮比赛中，选手甲、乙胜出的概率分别为 $\frac{3}{5}$ ， $\frac{3}{4}$ ；在第二轮比赛中，甲、乙胜出的概率分别为 $\frac{2}{3}$ ， $\frac{2}{5}$ .甲、乙两人在每轮比赛中是否胜出互不影响.

(1)、从甲、乙两人中选取1人参加比赛，派谁参赛赢得比赛的概率更大？

(2)、若甲、乙两人均参加比赛，求两人中至少有一人赢得比赛的概率.

查看试题解析
22. 如图，扇形OMN的半径为 $\sqrt{3}$ ，圆心角为 $\frac{π}{3}$ ， A为弧MN上一动点，B为半径上一点且满足 $∠ O B A = \frac{2 π}{3}$ .

(1)、若 $O B = 1$ ，求AB的长；

(2)、求△ABM面积的最大值.

查看试题解析