江西省名校2021-2022学年高一下学期数学期中调研试卷
试卷更新日期:2023-03-23 类型:期中考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 已知向量 , , , 则实数( )A、6 B、3 C、 D、-33. 扇形的弧长为12,面积为24,则圆心角的弧度数为( )A、4 B、3 C、2 D、14. 在 中,内角 , , 的对边分别为 , , ,且 , , ,则 ( )A、 B、 C、 D、5. 已知 , 则( )A、 B、 C、 D、6. 如图所示,每个小正方形的边长都是1,则下列说法正确的是( )
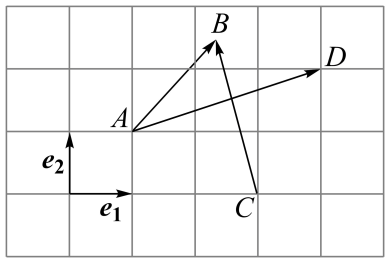 A、 , 是该平面所有向量的一组基底, B、 , 是该平面所有向量的一组基底, C、 , 不是该平面所有向量的一组基底, D、 , 不是该平面所有向量的一组基底,7. 某工厂的烟囱如图所示,底部为 , 顶部为 , 相距为的点 , 与点在同一水平线上,用高为的测角工具在 , 位置测得烟囱顶部在和处的仰角分别为 , .其中 , 和在同一条水平线上,在上,则烟囱的高( )
A、 , 是该平面所有向量的一组基底, B、 , 是该平面所有向量的一组基底, C、 , 不是该平面所有向量的一组基底, D、 , 不是该平面所有向量的一组基底,7. 某工厂的烟囱如图所示,底部为 , 顶部为 , 相距为的点 , 与点在同一水平线上,用高为的测角工具在 , 位置测得烟囱顶部在和处的仰角分别为 , .其中 , 和在同一条水平线上,在上,则烟囱的高( ) A、 B、 C、 D、8. 已知函数的部分图象如下图所示,先将的图象向右平移个单位长度(纵坐标不变),再将横坐标缩小为原来的(纵坐标不变),得到函数的图象,则( )
A、 B、 C、 D、8. 已知函数的部分图象如下图所示,先将的图象向右平移个单位长度(纵坐标不变),再将横坐标缩小为原来的(纵坐标不变),得到函数的图象,则( )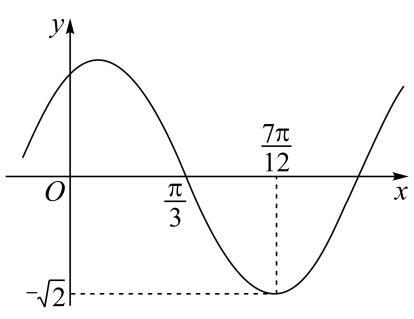 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 设 , 是虚数单位,复数.则下列说法正确的是( )A、若为实数,则 B、若为纯虚数,则 C、当时,在复平面内对应的点为 D、的最小值为10. 下列式子的值为的是( )A、 B、 C、 D、11. 在平面直角坐标系中,为坐标原点, , , 点 , 则下列说法正确的是( )A、 B、若是平行四边形,则 , C、若为的重心,则 , D、若 , , 则向量在向量上的投影向量为12. 已知函数 , 则下列结论正确的是( )A、在上单调递增 B、的图象的一条对称轴方程为 C、的最小正周期为 D、的最大值为
三、填空题
-
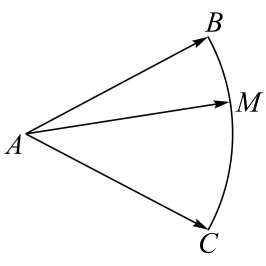
13. 化简14. 已知角的终边上有一点 , 则.15. 已知复数满足 , 则的最大值为.16. 如图所示,扇形中, , 点在上运动(包括端点、),且满足 , 则的最大值是.
四、解答题
-
17. 已知方程的两复数根分别为 , , 其中的虚部大于0(1)、求复数 , ;(2)、若复数 , 且 , 求实数的取值范围18.(1)、证明:(2)、求值:19. 在中,内角 , , 的对边分别为 , , , 且
请在① , ② , ③这三个条件中任选两个,将问题(1)补充完整,然后解答问题
注:如选择多种搭配方式分别解答,按第一个解答计分.
(1)、已知_______,计算的面积;(2)、当时,求的周长的最大值.