沪科版数学七年级下册第8章整式乘法与因式分解章末检测提升卷

试卷更新日期：2023-03-22 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列因式分解正确的是（）

A、 $- 3 x - 3 y = - 3 (x - y)$ B、 $x^{2} - x y + x = x (x - y)$ C、 $a x^{2} - a y^{2} = a (x^{2} - y^{2})$ D、 $a (x - y) - 2 b (y - x) = (x - y) (a + 2 b)$

查看试题解析
2. 若x+m与x﹣5的乘积中不含x的一次项，则m的值是（）

A、﹣5 B、0 C、1 D、5

查看试题解析
3. 已知5⁴－1能被20~30之间的两个整数整除，则这两个整数是（）

A、25，27 B、26，28 C、24，26 D、22，24

查看试题解析
4. 若 $a^{2} - 2 a - 1 = 0$ ，那么代数式 $(a + 2) (a - 2) - 2 a$ 的值为（）

A、 $- 1$ B、 $- 3$ C、1 D、3

查看试题解析
5. 已知 $x + \frac{1}{x} = 8$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值是（）

A、 $66$ B、 $64$ C、62 D、60

查看试题解析
6. 如图，有甲、乙、丙三种纸片各若干张，其中甲、乙分别是边长为a，b的正方形，丙是长为b，宽为a的长方形．若同时用甲、乙、丙纸片分别为4张、9张、12张拼成正方形，则拼成的正方形的边长为（）

A、a+2b B、a+3b C、2a+3b D、3a+2b

查看试题解析
7. 若 $(x - 2021) (x - 2022) = 6$ ，则 ${(2021 - x)}^{2} + {(2022 - x)}^{2}$ 的值是（）

A、11 B、12 C、13 D、14

查看试题解析
8. 下列因式分解正确的是（）

A、 $2 a x^{2} - 4 a x = 2 a (x^{2} - 2 x)$ B、 $- a x^{2} + 4 a x - 4 a = - a {(x - 2)}^{2}$ C、 $x^{2} + 2 x y + 4 y^{2} = {(x + 2 y)}^{2}$ D、 $- m^{2} + n^{2} = (- m + n) (- m - n)$

查看试题解析
9. 现有一张边长为 $a$ 的大正方形卡片和三张边长为 $b$ 的小正方形卡片 $(\frac{1}{2} a < b < a)$ 如图 $1$ ，取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $2$ ，再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $3$ ，已知图 $3$ 中的阴影部分的面积比图 $2$ 中的阴影部分的面积大 $2 a b - 15$ ，则小正方形卡片的面积是（）

A、 $10$ B、 $8$ C、 $2$ D、 $5$

查看试题解析
10. 为了书写简便，数学家欧拉引进了求和符号“ $\sum$ ”．如记 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + ... + (n - 1) + n MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaGaam4Aaiab
g2da9iaaigdacqGHRaWkcaaIYaGaey4kaSIaaG4maiabgUcaRiaac6
cacaGGUaGaaiOlaiabgUcaRmaabmaapaqaa8qacaWGUbGaeyOeI0Ia
aGymaaGaayjkaiaawMcaaiabgUcaRiaad6gaaSqaaiaadUgacqGH9a
qpcaaIXaaabaGaaeOBaaqdcqGHris5aaaa@5506@$ ， $\sum_{k = 3}^{n} (x + k) = (x + 3) + (x + 4) + ... + (x + n) MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaWaaeWaa8aa
baWdbiaadIhacqGHRaWkcaWGRbaacaGLOaGaayzkaaGaeyypa0Zaae
Waa8aabaWdbiaadIhacqGHRaWkcaaIZaaacaGLOaGaayzkaaGaey4k
aSYaaeWaa8aabaWdbiaadIhacqGHRaWkcaaI0aaacaGLOaGaayzkaa
Gaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSYaaeWaa8aabaWdbiaa
dIhacqGHRaWkcaWGUbaacaGLOaGaayzkaaaaleaacaWGRbGaeyypa0
JaaG4maaqaaiaad6gaa0GaeyyeIuoaaaa@5C66@$ ，已知 $\sum_{k = 2}^{n} [(x + k) (x - k + 1)] = 4 x^{2} + 4 x + m MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaawahabeWcpaqaa8qa
caWGRbGaeyypa0JaaGOmaaWdaeaapeGaamOBaaqdpaqaa8qacqGHri
s5aaGcdaWadaWdaeaapeWaaeWaa8aabaWdbiaadIhacqGHRaWkcaWG
RbaacaGLOaGaayzkaaWaaeWaa8aabaWdbiaadIhacqGHsislcaWGRb
Gaey4kaSIaaGymaaGaayjkaiaawMcaaaGaay5waiaaw2faaiabg2da
9iaaisdacaWG4bWdamaaCaaaleqabaWdbiaaikdaaaGccqGHRaWkca
aI0aGaamiEaiabgUcaRiaad2gaaaa@5A83@$ ，则m的值是（）

A、-50 B、-70 C、-40 D、-20

查看试题解析

二、填空题（每空3分，共15分）

11. 已知 $3^{x} = m$ ， $3^{y} = n$ ，用 $m$ 、 $n$ 表示 $3^{3 x + 4 y} - 5 \times 81^{x + 2 y}$ 为．

查看试题解析
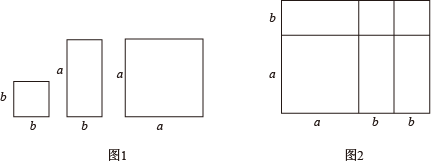
12. 若 $(x - 5) (x + a) = x^{2} - b x + 30$ ，则 $a =$ ， $b =$ ．

查看试题解析
13. 现有若干个长方形和正方形纸片如图1所示，将其拼成一个大长方形如图2，根据面积关系，我们有： $a^{2} + 3 a b + 2 b^{2} = (a + 2 b) (a + b)$ ，请利用拼图分解因式： $2 a^{2} + 5 a b + 2 b^{2} =$ .

查看试题解析
14. 若m²=n+2022，n²=m+2022（m≠n），那么代数式m³-2mn+n³的值．

查看试题解析
15. 如图，在面积为56的长方形ABCD中放入边长分别为6和4的正方形AEFG和CMNK，若三块阴影部分的面积之和为16，则长方形的周长为．

查看试题解析

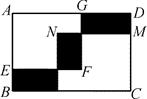
三、计算题（共2题，共18分）

16. 用简便方法计算下列各题：

(1)、 $103^{2} - 102 \times 104$ ；

(2)、 $99^{2}$ .

查看试题解析
17. 分解因式：

(1)、 $m^{4} - 16$ ；

(2)、 $a^{2} (x - y) + 2 a b (y - x) - b^{2} (y - x)$ .

查看试题解析

四、解答题（共2题，共12分）

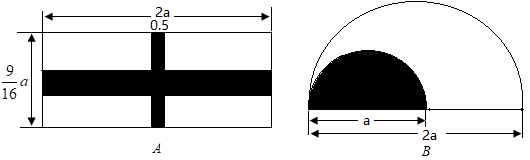
18. 已知多项式 $(x^{2} + p x + q) (x^{2} - 3 x + 2)$ 的结果中不含 $x^{3}$ 项和 $x^{2}$ 项，求 $p$ 和 $q$ 的值.

查看试题解析
19. 如图，公园里有A、B两个花坛，A花坛是长为20米，宽为 $\frac{9}{16} a$ 米的长方形，花坛中间16横竖各铺设一条小路（阴影部分），竖着的小路宽为0.5米，横着的小路宽为1米，剩余部分栽种花卉；B花坛是直径为 $2 a$ 米的半圆，其中修建一个半圆形水池（阴影部分），剩余部分栽种花卉，求B花坛比A花坛栽种花卉的面积大多少？（取 $π$ ）

查看试题解析

五、综合题（共3题，共25分）

20. 如图，有一块长（3a+b）米，宽（2a+b）米的长方形广场，园林部门要对阴影区城进行绿化，空白区城进行广场硬化，阴影部分是边长为（a+b）米的正方形.

(1)、计算广场上需要硬化部分的面积；

(2)、若a＝30，b＝10，求硬化部分的面积.

查看试题解析
21. [学习材料]——拆项添项法
在对某些多项式进行因式分解时，需要把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符号相反的项，这样的分解因式的方法称为拆项添项法．如：

例1：分解因式：x²+2x-3．

解：原式=x²+2x+1-1-3=（x+1）²-4=（x+1-2）（x+1+2）=（x-1）（x+3）．

例2：分解因式：x³+5x-6．

解：原式=x³-x+6x-6=x（x²-1）+6（x-1）=（x-1）（x²+x+6）．

[知识应用]请根据以上材料中的方法，解决下列问题：

(1)、分解因式：x²+14x-51= ．

(2)、化简： $\frac{x^{3} + 3 x^{2} - 4}{x + 2}$

查看试题解析
22. 把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积.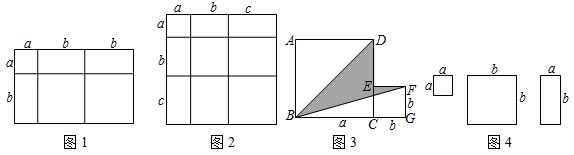

例如，由图1，可得等式：（a+2b）（a+b）＝a²+3ab+2b².

(1)、由图2，可得等式；

(2)、利用（1）所得等式，解决问题：已知a+b+c＝11，ab+bc+ac＝38，求a²+b²+c²的值.

(3)、如图3，将两个边长为a、b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF，若这两个正方形的边长a、b如图标注，且满足a+b＝10，ab＝20.请求出阴影部分的面积.

(4)、图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片，现有足量的这三种纸片.
①请在下面的方框中用所给的纸片拼出一个面积为2a²+5ab+2b²的长方形，并仿照图1、图2画出拼法并标注a、b；

②研究①拼图发现，可以分解因式2a²+5ab+2b²的值。

查看试题解析