沪科版数学七年级下册8.4因式分解同步练习

试卷更新日期：2023-03-22 类型：同步测试

进入出卷网下载

一、单选题（每题2分，共20分）

1. 下列各式从左到右的变形中，是因式分解且完全正确的是（　　）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $x^{2} - 2 x - 3 = x (x - 2) - 3$ C、 $x^{2} - 4 x + 4 = {(x - 2)}^{2}$ D、 $(x + 2) (x - 2) = x^{2} - 4$

查看试题解析
2. 对于①x-3xy=x(1-3y) ，②(x+3)(x-1)=x²+2x-3，从左到右的变形，表述正确的是（）

A、都是因式分解 B、①是因式分解，②是乘法运算 C、都是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
3. 下列多项式中不能运用公式法进行因式分解的是（）

A、 $- a^{2} + 4 b^{2}$ B、 $a^{2} - b^{2}$ C、 $- a^{2} + 2 a b - b {}_{2}$ D、 $- a^{2} + 2 a b + b^{2}$

查看试题解析
4. 下列多项式中，能运用平方差公式分解因式的是 $($ $)$

A、 $a^{2} + b^{2}$ B、 $2 a - b^{2}$ C、 $- a^{2} + b^{2}$ D、 $- a^{2} - b^{2}$

查看试题解析
5. 把 $2 x y - x^{2} - y^{2}$ 分解因式，结果正确的是（）.

A、 ${(x - y)}^{2}$ B、 ${(- x - y)}^{2}$ C、 $- {(x - y)}^{2}$ D、 $- {(x + y)}^{2}$

查看试题解析
6. 将下列各式因式分解，结果中不含因式a-1的是（）

A、 $2 a^{2} - 2 a$ B、 $a^{2} - 2 a - 3$ C、 $a^{3} - a$ D、 ${(a - 2)}^{2} + 2 (a - 2) + 1$

查看试题解析
7. 已知 $(19 x - 31) (13 x - 17) - (13 x - 17) (11 x - 23)$ 可因式分解成 $(a x + b) (8 x + c)$ ，其中a，b，c均为整数，则 $a + b + c =$ （）

A、-12 B、-32 C、38 D、72

查看试题解析
8. 已知二次三项式 $x^{2} - kx - 15$ 能分解成系数为整数的两个一次因式的积，则整数 $k$ 的取值范围有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知甲、乙、丙均为x的一次多项式，且其一次项的系数皆为正整数．若甲与乙相乘为x²－4，乙与丙相乘为x²＋15x－34，则甲与丙相加的结果为（）

A、2x＋19 B、2x－19 C、2x＋15 D、2x－15

查看试题解析
10. 现有边长为a的小正方形卡片一张，长宽分别为a、b的长方形卡片6张，边长为b的大正方形卡片10张，从这17张卡片中取出16张来拼图，能拼成长方形或正方形有（　　）

A、2种 B、3种 C、4种 D、5种

查看试题解析

二、填空题（每空3分，共15分）

11. 因式分解： $25 m^{2} - 10 m n + n^{2} =$ ．

查看试题解析
12. 一个长方形的长与宽分别为a，b，若周长为12，面积为5，则 $a b^{3} + 2 a^{2} b^{2} + a^{3} b$ 的值为．

查看试题解析
13. 如果 $1 + x + x^{2} = 0$ ，那么 $1 + x + x^{2} + x^{3} + \cdot \cdot \cdot + x^{99}$ 的值是．

查看试题解析
14. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式 $x^{4} - y^{4}$ ，因式分解的结果是 $(x - y) (x + y) (x^{2} + y^{2})$ ，若取 $x = 9$ ， $y = 9$ 时，则各个因式的值是： $(x - y) = 0$ ， $(x + y) = 18$ ， $(x^{2} + y^{2}) = 162$ ，于是就可以把“018162”作为一个六位数的密码．对于多项式 $x^{3} - 4 x y^{2}$ ，取 $x = 30$ ， $y = 10$ 时，写出一个用上述方法产生的密码．

查看试题解析
15. 阅读材料：若 $x^{3} + 2 x^{2} - 2 x + m (m$ 为常数 $)$ 有一个因式为 $(x - 1)$ ，则如何因式分解 $x^{3} + 2 x^{2} - 2 x + m$ ？
解：因为 $x^{3} + 2 x^{2} - 2 x + m$ 有一个因式为 $(x - 1)$ ，所以当 $x - 1 = 0$ 时， $x^{3} + 2 x^{2} - 2 x + m = 0$ ，于是把 $x = 1$ 代入 $x^{3} + 2 x^{2} - 2 x + m = 0$ 得 $1 + 2 - 2 + m = 0$ ，解得 $m = - 1$ ，原代数式变为 $x^{3} + 2 x^{2} - 2 x - 1$ ，接着可以通过列竖式做多项式除法的方式求出其它因式，如图所示，则因式分解 $x^{3} + 2 x^{2} - 2 x - 1 = (x - 1) (x^{2} + 3 x + 1)$

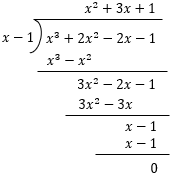
若 $x^{3} + 4 x^{2} + m x + 2 (m$ 为常数 $)$ 有一个因式为 $(x + 2)$ ，则因式分解 $x^{3} + 4 x^{2} + m x + 2 =$ .

查看试题解析

三、计算题（共12分）

16. 分解因式

(1)、 $4 a^{3} b - 2 a^{2} b^{2}$

(2)、 $x^{2} - 4 x + 4$

(3)、 $2 m^{2} - 18$

(4)、 $a^{2} + 7 a - 18$

查看试题解析

四、解答题（共3题，共15分）

17. 求证：对于任意自然数n，（n+7）²-（n-5）²都能被24整除.

查看试题解析
18. 已知 $x^{2} + 2 x + 1$ 是多项式 $x^{3} - x^{2} + a x + b$ 的一个因式，求a，b的值，并将该多项式因式分解.

查看试题解析
19. 阅读例题，解答问题：
例题：已知二次三项式x²+4x+m有一个因式是（x+1），求另一个因式及m的值．

解：设另一个因式为（x+n），得x²+4x+m＝（x+1）（x+n），则

x²+4x+m＝x²+（n+1）x+n ，

∴ ${\begin{matrix} n + 1 = 4 \\ m = n \end{matrix}$ ，

解得 ${\begin{matrix} m = 3 \\ n = 3 \end{matrix}$ ，

∴另一个因式（x+3），m的值为3．

问题：已知二次三项式2x²+x+k有一个因式是（2x﹣3），求另一个因式及k的值．

查看试题解析

五、综合题（共5题，共38分）

20. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
21. 下面是某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行因式分解的过程
解：设 $x^{2} - 4 x = y$ ，
原式 $= (y + 2) (y + 6) + 4$ （第一步）
$= y^{2} + 8 y + 16$ （第二步）
$= {(y + 4)}^{2}$ （第三步）
$= {(x^{2} - 4 x + 4)}^{2}$ （第四步）

(1)、该同学第二步到第三步运用了因式分解的____（填序号）．

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？．（填“是”或“否”）如果否，直接写出最后的结果．

(3)、请你模仿以上方法尝试对多项式 $(x^{2} - 2 x) (x^{2} - 2 x + 2) + 1$ 进行因式分解．

查看试题解析
22. 如图，用一张如图A的正方形硬纸板、三张如图B的长方形硬纸板、两张如图C的正方形硬纸板拼成一个长方形（如图D）.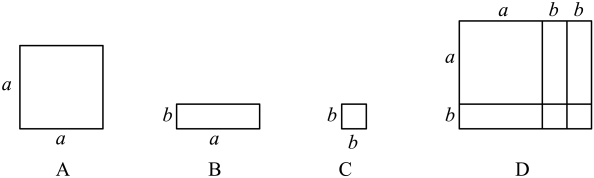

(1)、请用不同的式子表示图D的面积（写出两种即可）；

(2)、根据（1）所得结果，写出一个表示因式分解的等式.

查看试题解析
23. 阅读与思考：
分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式，比如：四项的多项式一般按照“两两”分组或“三一”分组，进行分组分解.

例 $1 ：$ “两两分组” $： a x + a y + b x + b y$ .

解：原式 $= (a x + a y) + (b x + b y)$

$= a (x + y) + b (x + y)$

$= (a + b) (x + y)$

例 $2 ：$ 三一分组” $： 2 x y + x^{2} - 1 + y^{2}$ .

解：原式 $= x^{2} + 2 x y + y^{2} - 1$

$= {(x + y)}^{2} - 1$

$= (x + y + 1) (x + y - 1) .$

归纳总结：用分组分解法分解因式要先恰当分组，然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下，解答下列问题：

分解因式：

(1)、 $x^{2} - x y + 5 x - 5 y$ ；

(2)、 $m^{2} - n^{2} - 4 m + 4$ .

查看试题解析
24. 阅读材料：利用公式法，可以将一些形如ax²+bx+c(a≠0)的多项式变形为a(x+m)²+n的形式，我们把这样的变形方法叫做多项式ax²+bx+c(a≠0)的配方法，运用多项式的配方法及平方差公式能对一些多项式进行因式分解.
例如：
$x^{2} + 4 x - 5 = x^{2} + 4 x + {(\frac{4}{2})}^{2} - {(\frac{4}{2})}^{2} - 5 = {(x + \frac{4}{2})}^{2} - 4 - 5 = {(x + 2)}^{2} - 9 = (x + 2 + 3) (x + 2 - 3) = (x + 5) (x - 1)$ 根据以上材料，解答下列问题

(1)、分解因式 $x^{2} + 2 x - 3$ ；

(2)、求多项式x²+6x-9的最小值；

(3)、已知a，b，c是△ABC的三边长，且满足 $a^{2} + b^{2} + c^{2} + 50 = 6 a + 8 b + 10 c$ ，求△ABC的周长.

查看试题解析