2023年中考数学复习考点一遍过——轴对称变换
试卷更新日期:2023-03-22 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点 , 点关于轴对称,则的平方根为( )A、1 B、2 C、 D、3. 在平面直角坐标系中,点A(-2,3)关于y轴对称的点的坐标( )A、(2,3) B、(2,-3) C、(-2,-3) D、(3,2)4. 点P关于x轴的对称点为 , 关于y轴的对称点为 , 那么点P的坐标是( )A、 B、 C、 D、5. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、等边三角形 B、平行四边形 C、等腰三角形 D、菱形6. 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1 , 再作与△A1B1C1关于x轴对称的△A2B2C2 , 则点A的对应点A2的坐标是( )
2. 点 , 点关于轴对称,则的平方根为( )A、1 B、2 C、 D、3. 在平面直角坐标系中,点A(-2,3)关于y轴对称的点的坐标( )A、(2,3) B、(2,-3) C、(-2,-3) D、(3,2)4. 点P关于x轴的对称点为 , 关于y轴的对称点为 , 那么点P的坐标是( )A、 B、 C、 D、5. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、等边三角形 B、平行四边形 C、等腰三角形 D、菱形6. 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1 , 再作与△A1B1C1关于x轴对称的△A2B2C2 , 则点A的对应点A2的坐标是( ) A、(-3,2) B、(2,-3) C、(1,-2) D、(-1,2)7. 如图,将矩形纸条折叠,折痕为 , 折叠后点 , 分别落在点 , 处,与交于点 , 已知 , 则的度数是( )
A、(-3,2) B、(2,-3) C、(1,-2) D、(-1,2)7. 如图,将矩形纸条折叠,折痕为 , 折叠后点 , 分别落在点 , 处,与交于点 , 已知 , 则的度数是( ) A、77° B、64° C、26° D、87°8. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( )
A、77° B、64° C、26° D、87°8. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( ) A、(4,10) B、(10,6) C、(10,4) D、(10,3)9. 如图,在正方形中,E 为边上一点,沿线段对折后,若比大 , 则的度数是( )
A、(4,10) B、(10,6) C、(10,4) D、(10,3)9. 如图,在正方形中,E 为边上一点,沿线段对折后,若比大 , 则的度数是( ) A、24度 B、20度 C、26度 D、30度10. 如图等边边长为 , D、E分别是、上两点,将沿直线折叠,点A落在处,在外,则阴影部分图形周长为( )
A、24度 B、20度 C、26度 D、30度10. 如图等边边长为 , D、E分别是、上两点,将沿直线折叠,点A落在处,在外,则阴影部分图形周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
11. 在平面直角坐标系中,点关于y轴对称后的点的坐标为 .12. 为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小彬计划制作一个如图所示的简易飞机模型.已知该模型是一个关于AC对称的轴对称图形,若AB=30cm,AC=22cm,则AD=cm.
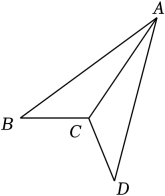 13. 如图, , 点是上一点,点与点关于对称,于点 , 若 , 则的长为 .
13. 如图, , 点是上一点,点与点关于对称,于点 , 若 , 则的长为 . 14. 如图,已知长方形纸片 , 点在上,将三角形沿折叠,点落在点处,连接并延长交于点 , 将对折,点落在直线上的点处,折痕为 , 则的度数是.
14. 如图,已知长方形纸片 , 点在上,将三角形沿折叠,点落在点处,连接并延长交于点 , 将对折,点落在直线上的点处,折痕为 , 则的度数是. 15. 已知点关于轴对称的点在第一象限,则的取值范围是 .16. 如图,矩形ABCD中,AB=6,AD=9,将四边形EFCD沿EF折叠得四边形EFC'D',点D′在AB上,若四边形EFCD的面积为24,则AD'的长度为 .
15. 已知点关于轴对称的点在第一象限,则的取值范围是 .16. 如图,矩形ABCD中,AB=6,AD=9,将四边形EFCD沿EF折叠得四边形EFC'D',点D′在AB上,若四边形EFCD的面积为24,则AD'的长度为 . 17. 如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=.
17. 如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=. 18. 如图,在平面直角坐标系中,将矩形沿直线折叠(点E在边上),折叠后点恰好落在边上的点F处.若点D的坐标为 , 则直线的解析式为.
18. 如图,在平面直角坐标系中,将矩形沿直线折叠(点E在边上),折叠后点恰好落在边上的点F处.若点D的坐标为 , 则直线的解析式为.
三、解答题(共7题,共66分)
-
19. 如图,的三个顶点都在方格纸的格点上,其中A点的坐标是 , B点的坐标是 , C点的坐标是 .
 (1)、作关于y轴对称的图形 , 点A、B、C的对应点分别为D、E、F;则点的坐标为 , 点F的坐标为 .(2)、在(1)的条件下,点P为x轴正半轴上的动点,当为等腰三角形时,请直接写出点P的横坐标 .20. 如图,在平面直角坐标系中, , , .
(1)、作关于y轴对称的图形 , 点A、B、C的对应点分别为D、E、F;则点的坐标为 , 点F的坐标为 .(2)、在(1)的条件下,点P为x轴正半轴上的动点,当为等腰三角形时,请直接写出点P的横坐标 .20. 如图,在平面直角坐标系中, , , . (1)、请画出△关于y轴对称的△;(2)、直接写出△的面积为;(3)、已知点D的横纵坐标都是整数,且△BCD和△BCA全等,请直接写出所有满足条件的点D的坐标;(D与A不重合)21. 如图,在平面直角坐标系中,、、.
(1)、请画出△关于y轴对称的△;(2)、直接写出△的面积为;(3)、已知点D的横纵坐标都是整数,且△BCD和△BCA全等,请直接写出所有满足条件的点D的坐标;(D与A不重合)21. 如图,在平面直角坐标系中,、、. (1)、在图中作出关于y轴对称的图形;(2)、写出 , 的坐标;(3)、求出的面积;22. 已知△ABC在平面直角坐标系中的位置如图所示,A,B,C三点均在格点上.
(1)、在图中作出关于y轴对称的图形;(2)、写出 , 的坐标;(3)、求出的面积;22. 已知△ABC在平面直角坐标系中的位置如图所示,A,B,C三点均在格点上.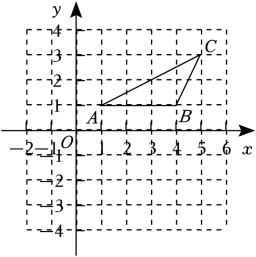 (1)、在直角坐标系内画出△ABC关于x轴对称的△A'B'C',并写出点A',B',C'的坐标;
(1)、在直角坐标系内画出△ABC关于x轴对称的△A'B'C',并写出点A',B',C'的坐标;
(2)、若点P与点C关于y轴对称,则点P的坐标为;
(3)、如果要使△ABD与△ABC全等,那么点D的坐标是.
23. 在△ABC中,AB=AC,∠BAC=90°. 过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD,直线BD交直线AP于点E. (1)、依题意补全图1;(2)、在图1中,若∠PAC=30°,求∠ABD的度数;(3)、若直线AP旋转到如图2所示的位置,请用等式表示线段EB,ED,BC之间的数量关系,并证明.24. 已知△ABC中,∠B= 60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ABE沿DE折叠,点A对应点为F点.
(1)、依题意补全图1;(2)、在图1中,若∠PAC=30°,求∠ABD的度数;(3)、若直线AP旋转到如图2所示的位置,请用等式表示线段EB,ED,BC之间的数量关系,并证明.24. 已知△ABC中,∠B= 60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ABE沿DE折叠,点A对应点为F点. (1)(1)、如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)、如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)、如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG的长.25. 如图,在网格中,每个小正方形的边长都为1.
(1)(1)、如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)、如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)、如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG的长.25. 如图,在网格中,每个小正方形的边长都为1.
( 1 )建立如图所示的平面直角坐标系,若点 , 则点C的坐标____;
( 2 )将向左平移5个单位,向上平移2个单位,则点C的坐标变为____;(无需画图)
( 3 )图中格点的面积是____;
( 4 )在x轴上找一点P,使得最小,请画出点P的位置.