沪科版数学七年级下册8.2整式乘法同步练习
试卷更新日期:2023-03-22 类型:同步测试
一、单选题(每题2分,共20分)
-
1. 下列运算正确的是( )A、x2+x3=x5 B、(x+1)(x﹣2)=x2+x﹣2 C、(1+2x)(2x﹣1)=1﹣4x2 D、﹣3a3÷a4=﹣2. 要使(x2+ax+1)(x-2)的结果中不含x2项,则a为( )A、-2 B、0 C、1 D、23. ( ) , 则括号内应填的代数式( )A、 B、 C、 D、4. 如果A、B都是关于x的单项式,且A·B是一个九次单项式,A+B是一个五次多项式, 那么A-B的次数( )A、一定是四次; B、一定是五次; C、一定是九次; D、无法确定.5. 若 , 则m与n的值分别是( )A、 B、1 C、 D、6. 一个长方形的面积为4a2﹣6ab+2a,它的长为2a,则宽为( )A、2a﹣3b B、4a﹣6b C、2a﹣3b+1 D、4a﹣6b+27. 计算(3x2y﹣xy2+ xy)÷( xy)的结果为( )A、﹣6x+2y﹣1 B、﹣6x+2y C、6x﹣2y D、6x﹣2y+18. 已知 , , , , , , , , ……, , , 的值为( )A、-48 B、-50 C、-98 D、-1009. 已知都是正数,如果( ) , 那么的大小关系是( )A、 B、 C、 D、不确定10. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
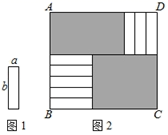 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共15分)
-
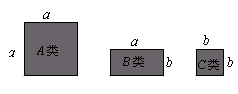
11. (-2a2)3÷a2 =.12. 已知二次三项式与的乘积展开式中不含项,也不含项,则.13. 用图中所示的正方形和长方形卡片若干张,拼成一个长为2a+b,宽为3a+2b的矩形,需要A类卡片张,B类卡片张,C类卡片张.
 14. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
14. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
则当 时,所捂多项式的值是
15. 已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),甲、乙的面积分别为S1 , S2 .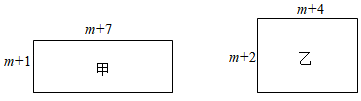 (1)、S1与S2的大小关系为:S1S2;(用“>”、“<”、“=”填空)(2)、若满足条件|S1﹣S2|<n≤2021的整数n有且只有4个,则m的值为 .
(1)、S1与S2的大小关系为:S1S2;(用“>”、“<”、“=”填空)(2)、若满足条件|S1﹣S2|<n≤2021的整数n有且只有4个,则m的值为 .三、计算题(共8分)
-
16. 计算:(1)、;(2)、(x-4y)(2x+3y)(3)、(4)、;
四、解答题(共3题,共16分)
-
17. 先化简后求值:已知a=4,b=-1,求代数式 的值.18. 小明在做一个多项式除以a的题时,由于粗心误认为乘a,结果是8a4b-4a3+2a2 , 那么你能知道正确的结果是多少吗?19. 如图,某市有一块长为 米,宽为 米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像,求绿化的面积是多少平方米?并求出当 时的绿化面积?

五、综合题(共4题,共41分)
-
20. 计算下列各式.(1)、.
.
.
……
(2)、根据以上规律,直接写出下式的结果:(3)、你能否由此归纳出一般性的结论:(其中 为正整数);
(4)、根据(2)的结论写出 的结果.21. 将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm,宽是3acm.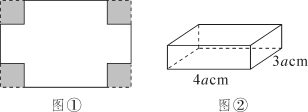 (1)、请用含有a的代数式表示图①中原长方形铁皮的面积;(2)、若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为cm2 , 则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?22. 在“整式乘法与因式分解”这一章的学习过程中,我们常采用构造几何图形的方法对代数式的变形加以说明.例如,利用图中边长分别为a,b的正方形,以及长为a,宽为b的长方形卡片若干张拼成图2(卡片间不重叠、无缝隙),可以用来解释完全平方公式: .
(1)、请用含有a的代数式表示图①中原长方形铁皮的面积;(2)、若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为cm2 , 则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?22. 在“整式乘法与因式分解”这一章的学习过程中,我们常采用构造几何图形的方法对代数式的变形加以说明.例如,利用图中边长分别为a,b的正方形,以及长为a,宽为b的长方形卡片若干张拼成图2(卡片间不重叠、无缝隙),可以用来解释完全平方公式: .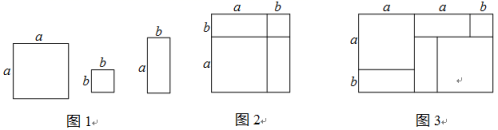
请你解答下面的问题:
(1)、利用图1中的三种卡片若干张拼成图 , 可以解释等式:;(2)、利用图1中三种卡片若干张拼出一个面积为的长方形ABCD,请你分析这个长方形的长和宽.23. 阅读材料:若满足 , 求的值.解:设 , , 则 , ,
所以
请仿照上例解决下面的问题:
(1)、问题发现:若x满足 , 求的值;(2)、类比探究:若x满足.求的值;(3)、拓展延伸:如图,正方形ABCD和正方形和MFNP重叠,其重叠部分是一个长方形,分别延长AD、CD,交NP和MP于H、Q两点,构成的四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形.若正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积为200.求正方形MFNP的面积(结果必须是一个具体数值).
-