浙江省台州市仙居县三校联考2021-2022学年八年级下学期期中考试数学试题

试卷更新日期：2023-03-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列的式子中是二次根式的是（）

A、 $\sqrt{- 1}$ B、 $\sqrt{3 - π}$ C、 $\sqrt[3]{8}$ D、 $\sqrt{3}$

查看试题解析
2. 判断下列几组数据中，可以作为直角三角形的三条边的是（）

A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6

查看试题解析
3. 如图，矩形ABCD中， $A B = 3$ ， $A D = 1$ ，点A、B在数轴上，点A表示数－1，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于点M，则点M表示的数为（）

A、 $\sqrt{10}$ B、 $\sqrt{10} - 1$ C、 $\sqrt{5}$ D、2.5

查看试题解析
4. 如图，在平行四边形ABCD中，AE平分∠DAB，∠AED＝26°，则∠C的度数为（）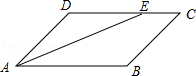

A、26° B、42° C、52° D、56°

查看试题解析
5. 用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）．

A、①②③ B、①④⑤ C、①②⑤ D、②⑤⑥

查看试题解析
6. 如图，▱ABCD的对角线AC ， BD交于点O ， AC⊥AB ， AB＝ $\sqrt{5}$ ，BO＝3，那么AC的长为（）

A、2 $\sqrt{2}$ B、 $\sqrt{5}$ C、3 D、4

查看试题解析
7. $\sqrt{a^{2} + 2 a + 1}$ -2的最小值是（）

A、-2 B、-1 C、0 D、2

查看试题解析
8. 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO．若∠DAC＝28°，则∠OBC的度数为（　　）

A、28° B、52° C、62° D、72°

查看试题解析
9. 如图，有一长、宽、高分别是5cm，4cm，4cm的长方体木块，一只蚂蚁沿如图所示路径从顶点A处在长方体的表面爬到长方体上和A相对的中点B处，则需要爬行的最短路径长为（）

A、 $\sqrt{85}$ cm B、 $\sqrt{61}$ cm C、 $\sqrt{97}$ cm D、 $\sqrt{\frac{281}{2}}$ cm

查看试题解析
10. 如图，在正方形ABCD中，点M是线段AB上的一个动点，点E是CM的中点，AE绕点E顺时针旋转90°得到EF，连接DE，DF.给出结论：① $D E = D F$ ；② $∠ C D F = 45 °$ ；③若正方形的边长为2，则CF的最小值是 $\sqrt{2}$ ；其中正确的结论有（）个.

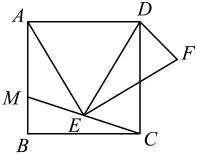A、0 B、3 C、2 D、1

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{2 + x}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
12. 请写出一个图象经过原点的函数的解析式.

查看试题解析
13. 如图，在平行四边形ABCD中，CE⊥AB于点E．若∠D=65°，则∠BCE=度．

查看试题解析
14. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $10$ 尺)，中部一处折断，竹梢触地面处离竹根 $3$ 尺，试问折断处离地面尺．

查看试题解析
15. 如图在正方形 $A B C D$ 中， $B E = 1$ ，将 $B C$ 沿 $C E$ 翻折，使点 $B$ 对应点刚好落在对角线 $A C$ 上，将 $A D$ 沿 $A F$ 翻折，使点 $D$ 对应点落在对角线 $A C$ 上，求 $E F =$ .

查看试题解析
16. 设n，k为正整数， $A_{1} = \sqrt{(n + 3) (n - 1) + 4}$ ， $A_{2} = \sqrt{(n + 5) A_{1} + 4}$ ， $A_{3} = \sqrt{(n + 7) A_{2} + 4}$ … $A_{k} = \sqrt{(n + 2 k + 1) A_{k - 1} + 4}$ ，已知 $A_{100} = 2021$ ，则 $n =$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{8} + | \sqrt{2} - 3 | + (π - 1)^{0}$ ；

(2)、 $(\sqrt{5} - \sqrt{2}) (\sqrt{5} + \sqrt{2}) + (\sqrt{3} - 2)^{2}$ .

查看试题解析
18. 如图，在平行四边形ABCD中，AE＝CF，求证：四边形BFDE是平行四边形．

查看试题解析

19. 今年发生了民航空难，令人痛心！2018年5月14日川航3U8633航班挡风玻璃在高空爆裂，机组临危不乱，果断应对.避免了一场灾难的发生，下面表格是成都当日海拔高度h（千米）与相应高度处气温t（℃）的关系【成都地处四川盆地，海拔高度较低，为方便计算，在此题中近似为0米】.

海拔高度h（千米）	0	1	2	3	4	5	…
气温t（℃）	20	14	8	2	$- 4$	$- 10$

根据上表，回答以下问题：

(1)、由上表可知海拔5千米的上空气温约为℃；

(2)、由表格中的规律请写出当日气温t与海拔高度h的关系式为.

(3)、如图是当日飞机下降过程中海拔高度与玻璃破了后立即返回地面所用的时间关系图.根据图像回答以下问题

①飞机在2千米高空水平面上大约盘旋了 ▲ 分钟；

②挡风玻璃在高空爆裂，机长在高空经历了很大的艰险.求当时飞机所处高空的气温为多少摄氏度？

查看试题解析

20. 图①、②均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形边长为1，点A、C在格点上.在给定的网格中按要求画图，所画图形的顶点均在格点上.
（ 1 ）在图①中画出以AC为底边的等腰直角三角形ABC；
（ 2 ）在图②中作一个平行四边形ACMN，使平行四边形ACMN的面积为（1）中 $△ A B C$ 面积的2倍.

查看试题解析
21. 如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，试求机器人行走的路程BC是多少？

查看试题解析
22. 如图，平行四边形ABCD中，对角线AC和BD交于点O ，过点A作AE⊥BC于点E ，延长BC到点F ，使CF＝BE ，连接DF和OF ．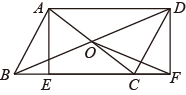

(1)、求证：四边形AEFD是矩形；

(2)、若AD＝5，CE＝3，∠ABF＝60°，求OF的长．

查看试题解析
23. 定义：我们将 $(\sqrt{a} + \sqrt{b})$ 与 $(\sqrt{a} - \sqrt{b})$ 称为一对“对偶式”，因为 $(\sqrt{a} + \sqrt{b}) (\sqrt{a} - \sqrt{b})$
$= {(\sqrt{a})}^{2} - {(\sqrt{b})}^{2} = a - b$ ，所以构造“对偶式”再将其相乘可以有效的将 $(\sqrt{a} + \sqrt{b})$ 中的“根号”去掉，于是二次根式除法可以这样计算：如 $\frac{2 + \sqrt{2}}{2 - \sqrt{2}} = \frac{{(2 + \sqrt{2})}^{2}}{(2 - \sqrt{2}) (2 + \sqrt{2})}$ .像这样，通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化.
根据以上材料，理解并运用材料提供的方法，解答以下问题：

(1)、对偶式 $2 + \sqrt{3}$ 与 $2 - \sqrt{3}$ 之间的关系为____.

A、互为相反数 B、互为倒数 C、绝对值相等 D、没有任何关系

(2)、已知 $x = \frac{1}{\sqrt{5} - 2}$ ， $y = \frac{1}{\sqrt{5} + 2}$ ，求 $\frac{x - y}{x^{2} y + x y^{2}}$ 的值.

(3)、解方程： $\sqrt{24 - x} - \sqrt{8 - x} = 2$ （提示：利用“对偶式”相关知识，令 $\sqrt{24 - x} + \sqrt{8 - x} = t$ ）.

查看试题解析
24. 如图，四边形ABCD是菱形，点M在CD边上，点N在菱形ABCD外部，且满足MN∥AD，CM＝MN，连接AN，CN，取AN的中点E，连接BE，AC.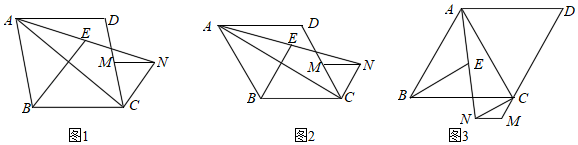

(1)、探究BE与AC的关系；

(2)、若∠ABC＝120°，探究线段BE、AD、CM所满足的等量关系；

(3)、若∠ABC＝60°，M在DC的延长线上时，其余条件不变，CM＝1，AD＝3，请求出BE的长度.

查看试题解析