浙江省台州市温岭市团队八校2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 以下四组木棒中，哪一组的三条能够刚好做成直角三角形的木架（）

A、7厘米，12厘米，15厘米 B、7厘米，12厘米，13厘米 C、8厘米，15厘米，16厘米 D、3厘米，4厘米，5厘米

查看试题解析
3. 在实数范围内， $\sqrt{3 - x}$ 有意义，则x的取值范围是（）

A、x＞3 B、x≥3 C、x≤3 D、x＜3

查看试题解析
4. 如图，在▱ABCD中，AD＝6，AB=4，DE平分∠ADC交BC于点E，则BE的长是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 如图一棵大树在离地面9米高的B处断裂，树顶A落在离树底部C的12米处，则大树断裂之前的高度为（）

A、9米 B、15米 C、21米 D、24米

查看试题解析
6. 若0＜x＜1，则x，x² ， $\sqrt{x}$ 的大小关系是（　　）

A、x＜x²＜ $\sqrt{x}$ B、x²＜x＜ $\sqrt{x}$ C、 $\sqrt{x}$ ＜x²＜x D、x＜ $\sqrt{x}$ ＜x²

查看试题解析
7. 为了研究特殊四边形，李老师制作了这样一个教具（如图1）：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C、B与D两点之间分别用一根橡皮筋拉直固定，课上，李老师右手拿住木条BC，用左手向右推动框架至AB⊥BC（如图2）观察所得到的四边形，下列判断正确的是（）

A、∠BCA＝45° B、AC＝BD C、BD的长度变小 D、AC⊥BD

查看试题解析
8. 如图，过平行四边形ABCD对角线交点O的直线交AD于E，交BC于F，若AB＝4，BC＝6，OE＝1.5，那么四边形EFCD周长是（）

A、16 B、15 C、14 D、13

查看试题解析
9. 如图，菱形ABCD的对角线AC，BD相交于点O，过点A作AH⊥BC于点H，连接OH，若OB＝4.5，S_菱形ABCD＝36，则OH的长为（）

A、3 B、3.5 C、4 D、4.5

查看试题解析
10. 如图，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG于点E，BF $∥$ DE且交AG于点F，若AB = 4EF，则 $S_{阴影} ：$ S_正方形ABCD的值为（）

A、9：16 B、17：32 C、17：36 D、18：35

查看试题解析

二、填空题

11. 计算： $\sqrt{8}$ =

查看试题解析
12. 如图，在正方形ABCD的外侧，作等边△ADE，则∠EBD= ．

查看试题解析
13. 如图，某研究性学习小组为测量学校A与河对岸工厂B之间的距离，在学校附近选一点C，利用测量仪器测得∠A＝60°，∠C＝90°，AC＝2km，据此可得学校与工厂之间的距离AB等于 km；

查看试题解析
14. 如图，矩形纸片ABCD中，AB＝4，BC＝6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF＝.

查看试题解析
15. 勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为．

查看试题解析
16. 如图，把一张矩形纸片ABCD沿EF，MN对折，得到五边形GEFNM.其中，顶点A与D重合于点G，重叠部分GHIJ为正方形，顶点I在EM上，若FN = $4 \sqrt{5}$ cm，EM =10cm，则BC长为cm.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{{(- 3)}^{2}} + {(\sqrt{5})}^{2} - \sqrt{16}$

(2)、 $(\sqrt{12} - \sqrt{\frac{1}{3}}) \div \sqrt{3}$

查看试题解析
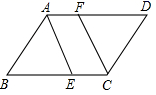
18. 已知x＝ $\sqrt{3}$ ﹣1，y＝1+ $\sqrt{3}$ ，求x²﹣xy+y²的值．

查看试题解析
19. 如图，在▱ABCD中，E、F分别是BC、AD上的点，且AE∥CF，AE与CF相等吗？说明理由.

查看试题解析
20. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点.
（ 1 ）在图①中，以格点为端点，画线段MN= $\sqrt{13}$ ；
（ 2 ）在图②中，以格点为顶点，画正方形ABCD，使它的面积为10.

查看试题解析
21. 如图，点E是正方形ABCD的边BC上的动点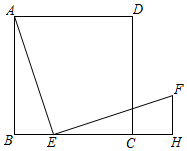， $∠ A E F = 90 °$ ，且 $E F = A E$ ， $F H ⊥ B H$ .

(1)、求证： $B E = C H$ ；

(2)、若 $A B = 3$ ， $B E = x$ ，用x表示DF的长.

查看试题解析
22. 四边形 $A B C D$ 是平行四边形，对角线 $A C$ ， $B D$ 交于点 $O$ .

(1)、如图是 $▱ A B C D$ 的一部分，请用尺规补全图形（不写作法，保留作图痕迹）；

(2)、如图，在射线 $B D$ 上作一点 $E$ ，使得 $∠ A C E =$ 60°若 $△ A C E$ 是等边三角形，求证： $▱ A B C D$ 是菱形；

(3)、在（2）的条件下，若 $∠ A E D = 2 ∠ E A D$ ，求证：菱形 $A B C D$ 是正方形.

查看试题解析
23. 已知在平面直角坐标系中，四边形ACBO是矩形，A（a，0）、B（0，b）满足 $\sqrt{a - b} + | a - 2 \sqrt{2} | = 0$ ， P是对角线AB上一动点，D是 $x$ 轴正半轴上一点，且PO =PD，DE⊥AB于E.

(1)、求a、b的值.

(2)、当P点运动时，PE的值是否发生变化？若变化，说明理由；若不变，请求PE的值.

(3)、若∠OPD =45°，求点D的坐标.

查看试题解析
24. 定义：四边形EFGH的四个顶点在 $▱$ ABCD四条边上（不与 $▱$ ABCD的顶点重合），我们称四边形EFGH为 $▱$ ABCD的内接四边形.

(1)、如图1，若 $▱$ ABCD的内接四边形EFGH为平行四边形，求证：AE=CG.

(2)、若 $∠ A = 60 °$ 的 $▱$ ABCD 的内接四边形EFGH为正方形，
①如图2，H为AD的中点，若AB =12，求AD的长；
②在①的条件下， $\frac{S_{Δ D H G} + S_{Δ A H E}}{S_{▱ A B C D}} =$ ▲ .

(3)、已知 $▱$ ABCD的内接四边形EFGH为平行四边形，且 $S_{▱ A B C D} = 2 S_{▱ E F G H}$ ，求证：点E、F、G、H中至少存在两个点是 $▱$ ABCD 边的中点.

查看试题解析