浙江省绍兴市柯桥区联盟校2021-2022学年八年级下学期期中考试数学试题
试卷更新日期:2023-03-22 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 最近北京2022年冬奥会的吉祥物“冰墩墩”成为了互联网的“顶流”,他呆萌的形象受到了人们的青睐,结合你所学知识,能够通过如图平移得到的选项是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 用配方法解一元二次方程x2-4x-7=0,可变形为( )A、(x-2)2=7 B、(x-2)2=11 C、(x+2)2=7 D、(x+2)2=114. 一组数据2,2,4,7,2,4的中位数是( )A、2 B、3 C、4 D、75. 四个一元二次方程:①x2−2x−3=0;②x2−2x+1=0;③x2−2x+2=0;④x2=0.其中没有实数根的方程的序号是( ).A、① B、② C、③ D、④6. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( )
3. 用配方法解一元二次方程x2-4x-7=0,可变形为( )A、(x-2)2=7 B、(x-2)2=11 C、(x+2)2=7 D、(x+2)2=114. 一组数据2,2,4,7,2,4的中位数是( )A、2 B、3 C、4 D、75. 四个一元二次方程:①x2−2x−3=0;②x2−2x+1=0;③x2−2x+2=0;④x2=0.其中没有实数根的方程的序号是( ).A、① B、② C、③ D、④6. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( ) A、40° B、50° C、60° D、70°7. 用反证法证明命题“四边形中至少有一个角是钝角或直角”时,首先应该假设这个四边形中( )A、有一个角是钝角或直角 B、每一个角都是锐角 C、每一个角都是直角 D、每一个角都是钝角8. 取一张长与宽之比为5:2的长方形纸板,剪去四个边长为的小正方形(如图),并用它做一个无盖的长方体形状的包装盒.要使包装盒的容积为(纸板的厚度略去不计),问这张长方形纸板的长与宽分别为多少厘米?若设这张长方形纸板的长为厘米,则由题意可列出的方程是( )
A、40° B、50° C、60° D、70°7. 用反证法证明命题“四边形中至少有一个角是钝角或直角”时,首先应该假设这个四边形中( )A、有一个角是钝角或直角 B、每一个角都是锐角 C、每一个角都是直角 D、每一个角都是钝角8. 取一张长与宽之比为5:2的长方形纸板,剪去四个边长为的小正方形(如图),并用它做一个无盖的长方体形状的包装盒.要使包装盒的容积为(纸板的厚度略去不计),问这张长方形纸板的长与宽分别为多少厘米?若设这张长方形纸板的长为厘米,则由题意可列出的方程是( ) A、 B、 C、 D、9. 如图,四边形ABCD中,AB=AD,AD//BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是( )
A、 B、 C、 D、9. 如图,四边形ABCD中,AB=AD,AD//BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是( ) A、 B、 C、2 D、10. 如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S▱ABCD=a,S▱EFGH=b(a<b),则S阴影为( )
A、 B、 C、2 D、10. 如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S▱ABCD=a,S▱EFGH=b(a<b),则S阴影为( )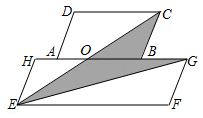 A、b﹣a B、 (b﹣a) C、 a D、 b
A、b﹣a B、 (b﹣a) C、 a D、 b二、填空题
-
11. 使 有意义的x的取值范围是 .12. 一个四边形四个内角的度数之比为1:1:0.6:1,则该四边形最小内角的度数为.13. 随机从甲、乙两块试验田中各抽取10株麦苗测量高度,计算平均数和方差的结果为 , , , , 则小麦长势比较整齐的试验田是.14. 一个十二边形有条对角线.15. 若关于x的一元二次方程的一个根是2,则另一个根为.16. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是。
 17. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD= , 则以A,B,C,D为顶点的四边形的面积是.
17. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD= , 则以A,B,C,D为顶点的四边形的面积是. 18. 在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程 的两个实数根,则△ABC的周长为 .19. 如图,在中, , 点、分别在边、上,且.将四边形沿直线翻折,点、的对应点分别是点、 , 如果四边形是平行四边形,那么度.
18. 在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程 的两个实数根,则△ABC的周长为 .19. 如图,在中, , 点、分别在边、上,且.将四边形沿直线翻折,点、的对应点分别是点、 , 如果四边形是平行四边形,那么度. 20. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是.
20. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是.
三、解答题
-
21. 计算:(1)、;(2)、(+)2﹣(+)(﹣).22. 选用适当的方法解下列方程.(1)、;(2)、x2+ 2x-5=0.23. 如图,▱ABCD的对角线AC,BD相交于点O,E,F分别是OB,OD的中点,连接AE,AF,CE,CF.
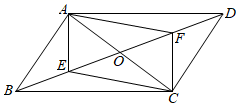 (1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5,求AE的长.24. 为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5,求AE的长.24. 为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题: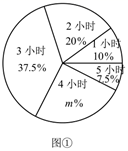
 (1)、该校抽查九年级学生的人数为 , 图①中的m值为;(2)、求统计的这组数据的众数、中位数和平均数.(3)、根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于 的学生人数.25. 某服装厂生产一批服装,2019年该类服装的出厂价是200元/件,2020年,2021年连续两年改进技术,降低成本,2021年该类服装的出厂价调整为162元/件.(1)、这两年此类服装的出厂价下降的百分比相同,求平均下降率.(2)、2021年某商场从该服装厂以出厂价购进若干件此类服装,以200元/件销售时,平均每天可销售20件.为了减少库存,商场决定降价销售.经调查发现,单价每降低5元,每天可多售出10件,如果每天盈利1150元,单价应降低多少元?26. 问题:如图,在中, , , ∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
(1)、该校抽查九年级学生的人数为 , 图①中的m值为;(2)、求统计的这组数据的众数、中位数和平均数.(3)、根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于 的学生人数.25. 某服装厂生产一批服装,2019年该类服装的出厂价是200元/件,2020年,2021年连续两年改进技术,降低成本,2021年该类服装的出厂价调整为162元/件.(1)、这两年此类服装的出厂价下降的百分比相同,求平均下降率.(2)、2021年某商场从该服装厂以出厂价购进若干件此类服装,以200元/件销售时,平均每天可销售20件.为了减少库存,商场决定降价销售.经调查发现,单价每降低5元,每天可多售出10件,如果每天盈利1150元,单价应降低多少元?26. 问题:如图,在中, , , ∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
答案:.
探究:
(1)、把“问题”中的条件“”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值.27.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2 ,P是AC上的一个动点.
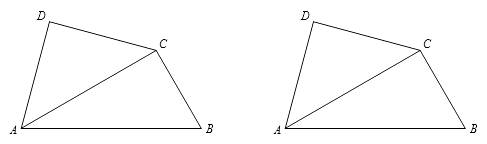 (1)、当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;(2)、当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;(3)、当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时平行四边形的面积.
(1)、当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;(2)、当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;(3)、当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时平行四边形的面积.