浙江省金华市义乌五校2021-2022学年八年级下学期期中考试数学试题

试卷更新日期：2023-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{3 x - 6}$ 有意义，则x的取值范围是（）

A、 $x \geq 0$ B、 $x \geq 2$ C、 $x \geq - 2$ D、 $x \leq 2$

查看试题解析
2. 下列方程中是一元二次方程的是（）

A、 $2 x - 1 = 0$ B、 $x^{2} + \frac{1}{x} - 2 = 0$ C、 $x^{2} - y^{2} = 0$ D、 $x^{2} - 2 x - 3 = 0$

查看试题解析
3. 甲、乙、两、丁四人各进行20次射击测试，他们的平均成绩相同，方差分别是 $s_{甲}^{2} = 0.8$ ， $s_{乙}^{2} = 0.6$ ， $s_{丙}^{2} = 0.9$ ， $s_{丁}^{2} = 1.0$ ，则射击成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 如图，所给图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是（）

A、 $(- \sqrt{16})^{2} = 16$ B、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ C、 $\sqrt{(- 4)^{2}} = - 4$ D、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$

查看试题解析
6. 如果关于x的一元二次方程 $k^{2} x^{2} - (2 k + 1) x + 1 = 0$ 有两个不相等的实数根，那么k的取值范围是（）

A、k>－ $\frac{1}{4}$ B、k>－ $\frac{1}{4}$ 且 $k \neq 0$ C、k<－ $\frac{1}{4}$ D、k $\geq$ － $\frac{1}{4}$ 且 $k \neq 0$

查看试题解析
7. 电影《长津湖》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，全国第一天票房约3亿元，假设以后每天票房按相同的增长率增长，第三天的票房收入约4亿元，若把增长率设为x，则下列方程正确的是（）

A、（1+x）²=4 B、3（1+x）²=4 C、3（1+x）³=4 D、（1+x）³=4

查看试题解析
8. 某班级共有41人，在一次体质测试中，有1人未参加集体测试，老师对集体测试的成绩按40人进行了统计，得到测试成绩分数的平均数是88，中位数是85.缺席集体测试的同学后面进行了补测，成绩为88分，关于该班级41人的体质测试成绩，下列说法正确的是（）

A、平均数不变，中位数变大 B、平均数不变，中位数无法确定 C、平均数变大，中位数变大 D、平均数不变，中位数变小

查看试题解析
9. 设关于x的方程 $a x^{2} + (a + 2) x + 9 a = 0$ ，有两个不相等的实数根 $x_{1} ， x_{2}$ ，且 $x_{1} < 1 < x_{2}$ ，那么实数a的取值范围是（）

A、 $a < - \frac{2}{11}$ B、 $\frac{2}{7} < a < \frac{2}{5}$ C、 $a > \frac{2}{5}$ D、 $- \frac{2}{11} < a < 0$

查看试题解析
10. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 交于点O， $A E$ 平分 $∠ B A D$ ，交 $B C$ 于点E，且 $∠ A D C = 60 °$ ， $A B = \frac{1}{2} B C$ ，连接 $O E$ ，下列结论：① $∠ C A D = 30 °$ ；② $O D = A B$ ；③ $S_{▱ A B C D} = A C \cdot C D$ ；④ $S_{四边形 O E C D} = \frac{3}{2} S_{△ A O D}$ ；⑤ $O E = \frac{1}{4} B C$ ，其中成立的个数为（）

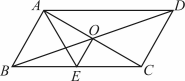A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 一元二次方程（x+1）²＝4的解为．

查看试题解析
12. 用反证法证明某一命题的结论“ $a > b$ ”时，应假设.

查看试题解析
13. 用配方法解关于x的一元二次方程 $x^{2} - 4 x - 3 = 0$ ，配方后的方程可以是.

查看试题解析
14. 一组数据的方差计算如下： $s^{2} = \frac{1}{6} [{(x_{1} - 2)}^{2} + {(x_{2} - 2)}^{2} + \cdot \cdot \cdot + {(x_{n} - 2)}^{2}]$ ，则这组数据的和是.

查看试题解析
15. 在 $▱ A B C D$ 中， $A E$ 平分 $∠ B A D$ 交 $B C$ 边于点 $E$ ， $D F$ 平分 $∠ A D C$ 交 $B C$ 边于点 $F$ ，若 $A D = 15$ ， $E F = 5$ ，则 $A B =$ .

查看试题解析
16. 已知：a，b，c都是正整数，且 $a + b + c = 342$ ， $a - b c = 331$ .则 $a b c$ 的最大值为，最小值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{5} - \sqrt{45} + 3 \sqrt{\frac{1}{5}}$ ；

(2)、 $(\sqrt{5} - \sqrt{2})^{2} + (2 + \sqrt{3}) (2 - \sqrt{3})$ .

查看试题解析
18. 解方程：

(1)、 ${(y - 1)}^{2} - 4 = 0$ ；

(2)、 $x^{2} + 2 x - 1 = 0$ .

查看试题解析
19. 已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点.

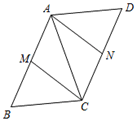(1)、求证：四边形AMCN是平行四边形；

(2)、若AC＝BC＝5，AB＝6，求四边形AMCN的面积.

查看试题解析
20. 图①、图②、图③、图④都是 $4 \times 4$ 的正方形网格，每个小正方形的边长均为1，每个小正方形顶点叫做格点．图①中的△ABC的顶点都在格点上．

(1)、沿BC边上的高将其剪成两个三角形，用这两个三角形在图②、图③、图④中各拼成一个平行四边形，所拼得的三个平行四边形不能够完全重合．

(2)、直接写出所拼得的平行四边形较长的对角线的长．

查看试题解析
21. 某学校第二课堂要创办“足球特色班”，大量的热爱足球的同学踊跃报名参加，但由于名额有限，所以需要考核选拔，考核的最终评价成绩是由足球知识、身体素质、足球技能三项成绩构成的，如果最终评价成绩80分以上（含80分），则评为“优秀”.下面表中是小张和小王两位同学的成绩记录：

足球知识
身体素质
足球技能
小张
70
90
80
小王
90
75

(1)、若按三项成绩的平均分记为最终评价成绩，请计算小张的最终评价成绩；

(2)、根据实际情况，学校决定足球知识、身体素质、足球技能三项成绩按 $1 ： 4 ： 5$ 的权重来确定最终评价成绩.
①请计算小张的最终评价成绩为多少分？
②小王在足球技能应该最少考多少分才能达到优秀？

查看试题解析
22. 一家水果店以每斤6元的价格购进某种水果若干斤，然后以每斤12元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出10斤.为保证每天至少售出360斤，水果店决定降价销售.

(1)、若将这种水果每斤的售价降低x元，则每天的销售量是多少斤（用含x的代数式表示）；

(2)、销售这种水果要想每天盈利1200元，那么水果店需将每斤的售价降低多少元？

查看试题解析
23. 如图，以n边形的n个顶点和它内部的x个点作为顶点，把原n边形分割成若干个互不重叠的小三角形.

(1)、以三角形的3个顶点和它内部的1个点作为顶点，把原三角形分割成3个互不重叠的小三角形；
以三角形的3个顶点和它内部的2个点作为顶点，把原三角形分割成5个互不重叠的小三角形；
以三角形的3个顶点和它内部的3个点作为顶点，可把原三角形分割成个互不重叠的小三角形；
以三角形的3个顶点和它内部的x个点作为顶点，可把原三角形分割成个互不重叠的小三角形（用含x的代数式表示）.

(2)、以四边形的4个顶点和它内部的1个点作为顶点，可把原四边形分割成4个互不重叠的小三角形；
以四边形的4个顶点和它内部的2个点作为顶点，可把原四边形分割成6个互不重叠的小三角形；
以四边形的4个顶点和它内部的3个点作为顶点，可把原四边形分割成个互不重叠的小三角形；
以四边形的4个顶点和它内部的x个点作为顶点，可把原四边形分割成个互不重叠的小三角形（用含x的代数式表示）.

(3)、以五边形的5个顶点和它内部的4个点作为顶点，可把原五边形分割成个互不重叠的小三角形；
以n边形的n个顶点和它内部的x个点作为顶点，可把原n边形分割成个互不重叠的小三角形（用含n，x的代数式表示）.

(4)、以n边形的n个顶点和它内部的x个点作为顶点，且 $x = \frac{1}{4} n$ （x，n均是整数），可把原n边形分割成3034个互不重叠的小三角形.求这个n边形的边数.

查看试题解析
24. 如图，在直角梯形 $A B C D$ 中， $A D ∥ B C$ ， $∠ A = 90 °$ ， $A B = 12$ ， $B C = 21$ ， $A D = 16$ .动点P从点B出发，沿射线 $B C$ 的方向以每秒3个单位长度的速度运动，动点Q从点D出发，在线段 $D A$ 上以每秒1个单位长度的速度向点A运动，点P、Q分别从点B、D同时出发，当点Q运动到点A时，点P随之停止运动，设运动的时间为t秒.

(1)、当t为何值时，P、Q两点之间的距离是13？

(2)、当t为何值时，以P、Q、C、D为顶点的四边形为平行四边形？

(3)、是否存在某一时刻t，使直线 $P Q$ 恰好把直角梯形 $A B C D$ 的周长和面积同时等分？如存在，求出此时t的值；若不存在，说明理由.

查看试题解析

	足球知识	身体素质	足球技能
小张	70	90	80
小王	90	75