浙江省金华市开发区2021-2022学年八年级下学期数学期中试题

试卷更新日期：2023-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{\frac{12}{7}}$ C、 $\sqrt{8}$ D、 $\sqrt{3}$

查看试题解析
3. 下列方程中是一元二次方程的是（）

A、2（x+1）=3 B、y²+x=0 C、x²+4=0 D、（x﹣2）²﹣x²=0

查看试题解析
4. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

尺码

$39$

$40$

$41$

$42$

$43$

平均每天销售数量（件）

$10$

$12$

$20$

$12$

$12$

该店主决定本周进货时，增加了一些 $41$ 码的衬衫，影响该店主决策的统计量是（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
5. 要使式子 $\frac{\sqrt{a + 2}}{a}$ 有意义，则a的取值范围是（）

A、a≠0 B、a＞-2且 a≠0 C、a＞2或 a≠0 D、a≥-2且 a≠0

查看试题解析
6. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使四边形AECF是平行四边形，则添加的条件不能是（）

A、AE＝CF B、BE＝FD C、BF＝DE D、∠1＝∠2

查看试题解析
7. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m².若设道路的宽为xm，则下面所列方程正确的是（）.

A、（32-2x）（20-x）=570 B、32x+2×20x=32×20-570 C、（32-x）（20-x）=32×20-570 D、32x+2×20x-2x²=570

查看试题解析
8. 若关于 $x$ 的方程 $x^{2} + 2 x - k = 0$ 没有实数根，则 $k$ 的值可以是（）.

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
9. 用反证法证明命题“三角形中必有一个内角小于或等于60°时，首先应假设这个三角形中（）

A、有一个内角小于60° B、有一个内角大于60° C、每一个内角都小于60° D、每一个内角都大于60°

查看试题解析
10. 如图，在平面直角坐标系中， $▱ O A B C$ 的边 $O C$ 落在x轴的正半轴上，且点 $C (4 ， 0) ， B (6 ， 2)$ ，直线 $y = 2 x + 1$ 以每秒1个单位的速度向下平移，经过（）秒该直线可将平行四边形 $O A B C$ 的面积平分.

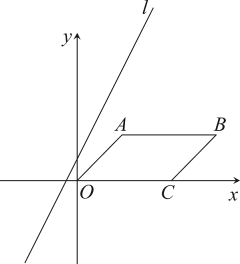A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 在平面直角坐标系中，点 $P (3 ， - 5)$ 关于原点对称的点的坐标是．

查看试题解析
12. 为了比较甲乙两种水稻秧苗是否出苗更整齐，每种秧苗各取 $10$ 株分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙方差分别是 $3.9$ 、 $15.8$ ，则（填“甲”或“乙”）秧苗出苗更整齐.

查看试题解析
13. 若一个n边形的内角和是外角和的3倍，则n=.

查看试题解析
14. 已知 $y = \sqrt{x - 4} + \sqrt{4 - x} - 5$ ，则 ${(x + y)}^{2021} =$ .

查看试题解析
15. 对于三个数 $a ， b ， c$ ，我们规定用 $M {a ， b ， c}$ 表示这三个数的平均数，用 $m i n {a ， b ， c}$ 示这三个数中最小的数.例如： $M {- 1 ， 2 ， 3} = \frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ， $m i n {- 1 ， 2 ， 3} = - 1$ ，如果 $M {3 ， 2 x + 1 ， 4 x - 1} = m i n {2 ， - x + 3 ， 5 x}$ ，那么x=.

查看试题解析
16. 如图，平行四边形ABCD，点F是BC上的一点，连接AF，∠FAD＝60°，AE平分∠FAD，交CD于点E，且点E是CD的中点，连接EF，已知AD＝5，CF＝3，则EF＝.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{{(- 1)}^{2}} - {(\sqrt{3})}^{2} + \sqrt{12}$ ；

(2)、 $(2 - \sqrt{2}) (3 + 2 \sqrt{2})$ .

查看试题解析
18. 解下列方程：

(1)、 $x^{2} = 3 x$ ；

(2)、 $x^{2} + 2 x - 1 = 0$ .

查看试题解析
19. 在抗击“新冠肺炎疫情”的日子里，某校积极开展“停课不停学”的线上教学活动.为了解全校 $1200$ 名学生一周内平均每天在家进行体育锻炼时间的情况，随机调查了该校 $100$ 名学生一周内平均每天在家进行体育锻炼时间的情况，结果如表：
时间 $（$ 分 $）$
$15$
$20$
$25$
$30$
$35$
$40$
$45$
$50$
$55$
$60$
人数
$16$
$24$
$14$
$10$
$8$
$6$
$8$
$4$
$6$
$4$
完成下列问题：

(1)、根据统计表信息，写出这 $100$ 名学生一周内平均每天在家体育锻炼时间的中位数和众数.

(2)、请估计该校一周内平均每天在家体育锻炼时间不少于 $35$ 分钟的学生大约有多少人？

查看试题解析
20. 如图，在▱ABCD中，点E，点F在对角线AC上且AE＝EF＝FC.

(1)、求证：四边形DEBF是平行四边形；

(2)、若∠CDE＝90°，DC＝8，DE＝6，求▱DEBF的周长.

查看试题解析
21. 某商场在去年底以每件 $120$ 元的进价购进一批同型号的服装，一月份以每件 $150$ 元的售价销售了 $320$ 件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计知三月份的销量达到了 $500$ 件.

(1)、求二、三月份服装销售量的平均月增长率；

(2)、从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价 $5$ 元，月销售量增加 $10$ 件，当每件降价多少元时，四月份可获利 $10400$ 元？

查看试题解析
22. 已知 $x_{1} ， x_{2}$ 是关于x的一元二次方程 $x^{2} - 2 (m + 1) x + m^{2} + 10 = 0$ 的两实数根.

(1)、求m的取值范围；

(2)、已知等腰 $△ A B C$ 的一边长为 $7$ ，若 $x_{1} ， x_{2}$ 恰好是 $△ A B C$ 另外两边的边长，求m的值和 $△ A B C$ 的周长.

查看试题解析
23. 在四边形 $A B C D$ 中， $A B ∥ C D ， ∠ B C D = 90 ° ， A B = A D = 10 c m ， B C = 8 c m$ ，点P从点A出发，沿折线 $A B C D$ 方向以 $3 c m / s$ 的速度匀速运动；点Q从点D出发，沿线段 $D C$ 方向以 $2 c m / s$ 的速度匀速运动.已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为 $t (s)$ .

(1)、求 $C D$ 的长；

(2)、当四边形 $P B Q D$ 为平行四边形时，求四边形 $P B Q D$ 的周长；

(3)、在点P、Q的运动过程中，是否存在某一时刻，使得 $△ B P Q$ 的面积为 $16 c m^{2}$ ？若存在，请求出所有满足条件的t的值；若不存在，请说明理由.

查看试题解析
24. 我们规定：有一组邻边相等，且这组邻边的夹角为 $60 °$ 的凸四边形叫做“准筝形”.

(1)、如图1，在四边形 $A B C D$ 中， $∠ A = 120 °$ ， $∠ C = 150 °$ ， $∠ D = 30 °$ ， $A B = B C = 2$ ，则 $A D =$ ； $C D =$ .

(2)、小军同学研究“准筝形”时，思索这样一道题：如图 $2$ ， “准筝形” $A B C D ， A D = B D ， ∠ B A D = ∠ B C D = 60 ° ， B C = 5 ， C D = 3$ ，求 $A C$ 的长.
小军研究后发现，可以 $C D$ 为边向外作等边三角形，构造手拉手全等模型，用转化的思想来求 $A C ．$ 请你按照小军的思路求 $A C$ 的长.

(3)、如图 $3$ ，在 $△ A B C$ 中， $∠ A = 45 ° ， ∠ A B C = 120 ° ， B C = 2 \sqrt{3}$ ，设D是 $△ A B C$ 所在平面内一点，当四边形 $A B C D$ 是“准筝形”时，请直接写出四边形 $A B C D$ 的面积.

查看试题解析

尺码	$39$	$40$	$41$	$42$	$43$
平均每天销售数量（件）	$10$	$12$	$20$	$12$	$12$

时间 $（$ 分 $）$	$15$	$20$	$25$	$30$	$35$	$40$	$45$	$50$	$55$	$60$
人数	$16$	$24$	$14$	$10$	$8$	$6$	$8$	$4$	$6$	$4$