浙江省金华市金东区孝顺教育集团2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-21 类型:期中考试
一、单选题
-
1. 下列方程中,属于一元二次方程的是( )A、x+y=1 B、x2+x=1 C、x+ =1 D、x3+x2=12. 以下图案属于中心对称图形的是( )A、
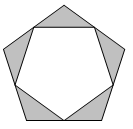 B、
B、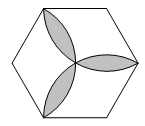 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、标准差5. 用反证法证明“”,应假设( )A、 B、 C、 D、6. 已知一元二次方程 , 下列判断正确的是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程无实数根 D、该方程根的情况无法确定7. 一个多边形的每个内角都等于108°,则这个多边形的边数为( ).A、5 B、6 C、7 D、88. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、标准差5. 用反证法证明“”,应假设( )A、 B、 C、 D、6. 已知一元二次方程 , 下列判断正确的是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程无实数根 D、该方程根的情况无法确定7. 一个多边形的每个内角都等于108°,则这个多边形的边数为( ).A、5 B、6 C、7 D、88. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( ) A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分9. 《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )A、 B、 C、 D、10. 矩形纸片按如图1的方式分割成三个直角三角形①,②,③,又把这三个直角三角形按如图2的方式重叠放置在一起,其中直角三角形①的斜边一端点恰好落在直角三角形②的斜边上,若 , 则图2中的长为( )
A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分9. 《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )A、 B、 C、 D、10. 矩形纸片按如图1的方式分割成三个直角三角形①,②,③,又把这三个直角三角形按如图2的方式重叠放置在一起,其中直角三角形①的斜边一端点恰好落在直角三角形②的斜边上,若 , 则图2中的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使 有意义的x的取值范围是 .12. 甲、乙两位同学在几次测验中,平均分都是分,甲的方差是 , 乙的方差是 , 你认为成绩较稳定的是.(填“甲”或“乙”)13. 如图,在平行四边形中,交于O,试添加一个条件使四边形成为矩形.你添加的条件是.(只填一个即可)
 14. 已知x=1是方程的一个根,则2a-2b+2024=.15. 如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=4,BC=5,则四边形EFGH的周长是.
14. 已知x=1是方程的一个根,则2a-2b+2024=.15. 如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=4,BC=5,则四边形EFGH的周长是. 16. 如图1是伸缩式雨棚的实物图,由骨架与伞面两部分组成,可抽象成矩形ABCD(如图2),其中实线部分表示雨棚的骨架,矩形ABCD为雨棚的伞面,CD固定不动,当横杆AB自由伸缩时,骨架与伞面也跟着伸缩,伸缩过程中伞面ABCD始终是矩形.若点D,G,E在一条直线上时,雨棚伞面面积最大.现测得AB=5m,DG=CH=2m,GE=HF=1.5m,AE=BF=0.5m.
16. 如图1是伸缩式雨棚的实物图,由骨架与伞面两部分组成,可抽象成矩形ABCD(如图2),其中实线部分表示雨棚的骨架,矩形ABCD为雨棚的伞面,CD固定不动,当横杆AB自由伸缩时,骨架与伞面也跟着伸缩,伸缩过程中伞面ABCD始终是矩形.若点D,G,E在一条直线上时,雨棚伞面面积最大.现测得AB=5m,DG=CH=2m,GE=HF=1.5m,AE=BF=0.5m. (1)、当雨棚伞面面积最大时,AD=m;(2)、当∠DGE=90°时,雨棚伞面的面积等于.
(1)、当雨棚伞面面积最大时,AD=m;(2)、当∠DGE=90°时,雨棚伞面的面积等于.三、解答题
-
17. 计算:.18. 解方程:2x2-3x=0.19. 如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上,试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形
 (1)、以A为顶点的平行四边形;(2)、以A为对角线交点的平行四边形.20. 如图,在▱ABCD中,E、F分别是BC、AD上的点,且AE∥CF,AE与CF相等吗?说明理由.
(1)、以A为顶点的平行四边形;(2)、以A为对角线交点的平行四边形.20. 如图,在▱ABCD中,E、F分别是BC、AD上的点,且AE∥CF,AE与CF相等吗?说明理由. 21. 我市开展“创全国文明城市”活动,学校倡议学生利用双休日参加志愿者服务活动,为了解同学们的活动情况,学校随机调查了部分同学的活动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
21. 我市开展“创全国文明城市”活动,学校倡议学生利用双休日参加志愿者服务活动,为了解同学们的活动情况,学校随机调查了部分同学的活动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题: (1)、这次抽样共调查了 名学生,并补全条形统计图.(2)、这组数据的众数是小时,中位数是小时.(3)、求这组数据的平均数.22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不小于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件(1)、若降价5元,则平均每天的销售量为件,每天的盈利是元;(2)、当每件商品降价多少元时,该商店每天的盈利为1200元?23. 类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)、这次抽样共调查了 名学生,并补全条形统计图.(2)、这组数据的众数是小时,中位数是小时.(3)、求这组数据的平均数.22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不小于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件(1)、若降价5元,则平均每天的销售量为件,每天的盈利是元;(2)、当每件商品降价多少元时,该商店每天的盈利为1200元?23. 类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.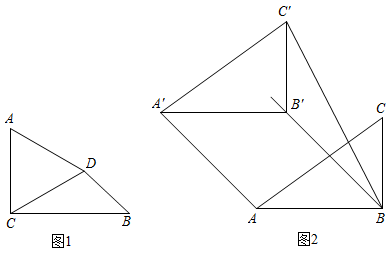 (1)、如图1,已知∠ACB=90°,AC=4, , 将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)、如图1,已知∠ACB=90°,AC=4, , 将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.①四边形ACBD (填“是”或“不是”)等邻边四边形;
②求线段DB的长度.
(2)、如图2,在△ABC中,∠ABC=90°,AB=4,BC=3,将Rt△ABC沿∠B的平分线方向平移得到 , 连接 , .若平移后的四边形是“等邻边四边形”,则平移的距离(即线段的长)为.24. 如图1,在平面直角坐标系中,点A(0,6),点B是x轴正半轴上的一个动点,连接AB,取AB的中点M,将线段MB绕着点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(2t,0).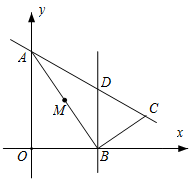 (1)、当t=2时,点M的坐标是.(2)、求点C的坐标(用含t的代数式表示).(3)、在点B的运动过程中,
(1)、当t=2时,点M的坐标是.(2)、求点C的坐标(用含t的代数式表示).(3)、在点B的运动过程中,①若四边形AOBD为矩形,求t的值;
②若△ABD为等腰三角形,求t的值.