浙江省温州市瓯海区第三教育集团2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示， $∠ B$ 与 $∠ 2$ 是一对（）

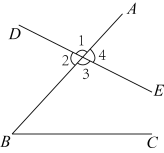A、同位角 B、内错角 C、同旁内角 D、对顶角

查看试题解析
2. 在下列图形中，不能通过其中一个四边形平移得到的是（）

A、 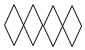B、 C、 D、

查看试题解析
3. 可乐中含有大量的咖啡因，世界卫生组织建议青少年每天咖啡因的摄入量不能超过 $0.000085 kg$ .则 $0 .000085$ 这个数字可用科学记数法表示为（）

A、 $8.5 \times 10^{- 5}$ B、 $85 \times 10^{- 6}$ C、 $8.5 \times 10^{- 6}$ D、 $0.85 \times 10^{- 4}$

查看试题解析
4. 已知 ${\begin{array}{l} x = - 3 \\ y = 10 \end{array}$ 是方程 $x + a y = 17$ 的一个解，则 $a$ 的值为 $($ $)$

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、2 D、-1

查看试题解析
5. 下列运算中，正确的是（）

A、（a²）³＝a⁵ B、a²+a³＝a⁵ C、a⁶÷a²＝a⁴ D、a·a³＝a³

查看试题解析
6. 如图所示，在下列四组条件中，不能判定 $A D ∥ B C$ 的是（）

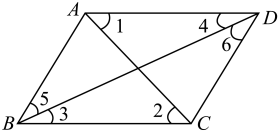A、∠1＝∠2 B、∠BAD+∠ABC＝180° C、∠3＝∠4 D、∠5＝∠6

查看试题解析
7. 下列各式中，不能用平方差公式计算的是（）

A、（a-b）（a+b） B、（-a+b）（-b-a） C、（-2x-3y）（2x+3y） D、（-2x+3y）（3y+2x）

查看试题解析
8. 如图，CE平分∠ACB，过点E作 $E F ∥ B C$ ，交AC于点F.已知∠AFE＝68°，则∠FEC的度数为（）

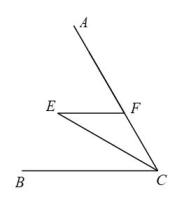A、68° B、34° C、32° D、22°

查看试题解析
9. 若方程组 ${\begin{array}{l} 5 x - 3 y = 7 \\ 7 x - 5 y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 6.5 \\ y = 8.5 \end{array}$ ，则方程组 ${\begin{array}{l} 5 (x - 13) - 3 (y + 1) = 7 \\ 7 (x - 13) - 5 (y + 1) = 3 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 19.5 \\ y = 9.5 \end{array}$ B、 ${\begin{array}{l} x = 19.5 \\ y = 7.5 \end{array}$ C、 ${\begin{array}{l} x = - 6.5 \\ y = 9.5 \end{array}$ D、 ${\begin{array}{l} x = - 6.5 \\ y = 7.5 \end{array}$

查看试题解析
10. 甲、乙、丙三名工人共承担装搭一批零件.已知甲乙丙丁四人聊天时的对话信息如下：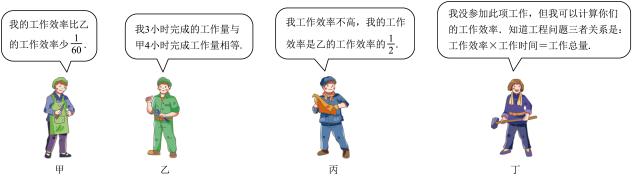
如果每小时只安排1名工人，那么按照甲、乙、丙的轮流顺序至完成工作任务，共需（）小时.

A、20 B、21 C、19 $\frac{1}{4}$ D、19 $\frac{3}{4}$

查看试题解析

二、填空题

11. 计算：-3a·（4b）＝.

查看试题解析
12. 已知2x+3y=1，用关于x的代数式表示y，则y=.

查看试题解析
13. 已知（x+p）（x+q）＝x²-6x+8，则p+q＝.

查看试题解析
14. 端午节时，王老师用72元钱买了荷包和五彩绳共20个.其中荷包每个4元，五彩绳每个3元，设王老师购买荷包x个，五彩绳y个，根据题意，列出的方程组是.

查看试题解析
15. 已知a^m＝4，aⁿ＝5，则 $a^{2 m + n}$ 的值是．

查看试题解析
16. 某中学开展“筑梦冰雪，相约冬奥”的学科活动，设计几何图形作品表达对冬奥会的祝福.小冬以长方形ABCD的四条边为边向外作四个正方形，设计出“中”字图案，如图所示.若四个正方形的周长之和为32，面积之和为12，则长方形ABCD的面积为 .

查看试题解析
17. “格子乘法”作为两个数相乘的一种计算方法最早在 $15$ 世纪由意大利数学家帕乔利提出，在明代的《算法统宗》一书中被称为“铺地锦”.如图1，计算 $47 \times 51$ ，将乘数 $47$ 计入上行，乘数 $51$ 计入右行，然后以乘数 $47$ 的每位数字乘以乘数 $51$ 的每位数字，将结果计入相应的格子中，最后按斜行加起来，得 $2397$ .如图 $2$ ，用“格子乘法”表示两个两位数相乘，则 $a$ 的值为.

查看试题解析

三、解答题

18. 计算及化简：

(1)、 $(- \frac{1}{2})^{- 1} + (π - 3.14)^{0}$ ；

(2)、 $[a^{2} - a (4 a^{2} + a - 3 b)] \div (2 a)$ .

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} 3 x + y = 10 \\ y = 2 x \end{array}$ ；

(2)、 ${\begin{array}{l} x - 2 y = 2 \\ \frac{3}{8} x - \frac{1}{4} y = 1 \end{array}$ .

查看试题解析
20. 如图，在正方形网格中，每个小正方形的边长均为1，三角形ABC的顶点均在格点上，将三角形ABC向右平移4格，再向上平移2格，得到三角形 $A^{'} B^{'} C^{'}$ （点A，B，C的对应点分别为 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ）.

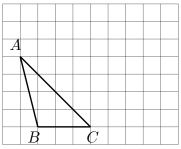(1)、请画出平移后的三角形 $A^{'} B^{'} C^{'}$ ，并标明对应字母；

(2)、若将三角形ABC经过一次平移得到图（1）中的三角形 $A^{'} B^{'} C^{'}$ ，则线段AB在平移过程中扫过区域的面积为.

查看试题解析
21. 如图，某小区有一块长为（2a+3b）米，宽为（2a-3b）米的长方形地块，角上有四个边长为（a-b）米的小正方形空地，开发商计划将阴影部分进行绿化.

(1)、用含有a、b的式子表示绿化的总面积（结果写成最简形式）.

(2)、若a＝25，b＝10，绿化成本为50元/平方米，则完成绿化共需要多少元钱？

查看试题解析
22. 如图，一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A，G，H，D，且∠1＝∠2，∠B＝∠C.

(1)、判断EC与BF的位置关系，并说明理由；

(2)、若∠BFC＝3∠B-40°，求∠C的度数.

查看试题解析
23. 三垟瓯柑享誉世界.水果商贩李大姐从三垟柑农处批发进货，她获知Ⅰ级瓯柑每箱60元，Ⅱ级瓯柑每箱40元.李大姐本次购得的Ⅰ级瓯柑比Ⅱ级瓯柑多10箱，共花费了3100元.

(1)、求Ⅰ级瓯柑和Ⅱ级瓯柑各购买了多少箱？

(2)、李大姐有甲、乙两家店铺，每售出一箱不同级别的瓯柑获利不同，具体见表.

Ⅰ级瓯柑每箱获利（单位：元/箱）
Ⅱ级瓯柑每箱获利（单位：元/箱）
甲店
15
20
乙店
12
16
设李大姐将购进的瓯柑分配给甲店Ⅰ级瓯柑a箱，Ⅱ级瓯柑b箱，其余都分配给乙店.因善于经营，两家店都很快卖完了这批瓯柑.
①李大姐在甲店获利660元，则她在乙店获利多少元？
②若李大姐希望获得总利润为1000元，则分配给甲店共 ▲ 箱水果.（直接写出答案）

查看试题解析

	Ⅰ级瓯柑每箱获利（单位：元/箱）	Ⅱ级瓯柑每箱获利（单位：元/箱）
甲店	15	20
乙店	12	16