浙江省台州市五校联考2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案是由图中所示的图案通过平移后得到的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列各数： $π ， \frac{5}{12} ， 5 ， 3.121212 \dots ， \sqrt{7}$ 中无理数的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 点P（−5，3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，下列条件中，不能判断直线a//b的是（）

A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°

查看试题解析
5. 在平面直角坐标系内，线段CD是由线段AB平移得到的，点A（-2，3）的对应点为C（2，5），则点B（-4，-1）的对应点D的坐标为（）

A、 $(- 8 ， - 3)$ B、 $(4 ， 2)$ C、 $(0 ， 1)$ D、 $(1 ， 8)$

查看试题解析
6. 下列各式正确的是（）

A、 $(- 3)^{2} = 6$ B、 $\sqrt[3]{8} = \pm 2$ C、 $- 1^{4} = - 1$ D、 $\sqrt{9} = \pm 3$

查看试题解析
7. 下列命题是假命题的是（）

A、两条直线被第三条直线所截，内错角相等 B、实数和数轴上的点是一一对应的 C、坐标平面内的点与有序实数对是一一对应的 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
8. 如图，数轴上有A，B，C，D四点，则所表示的数与 $\sqrt{11}$ -2最接近的是（）

A、点A B、点B C、点C D、点D

查看试题解析
9. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A₁（0，1），A₂（1，1），A₃（1，0），A₄（2，0），…那么点A₂₀₂₂的坐标为（）.

A、（1009，0） B、（1010，0） C、（1010，1） D、（1011，1）

查看试题解析
10. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内CD上方的一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β.下列各式：①α+β，②α﹣β，③β﹣α，④180°﹣α﹣β，⑤360°﹣α﹣β中，∠AEC的度数可能是（　　）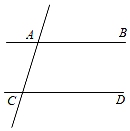

A、①②③ B、①②④⑤ C、①②③⑤ D、①②③④⑤

查看试题解析

二、填空题

11. $\sqrt{81}$ 的平方根是．

查看试题解析
12. 如图，从位置P到直线公路MN共有四条小道PA、PB、PC、PD，若用相同的速度行走，能最快到达公路MN的小道是，理由是．

查看试题解析
13. 已知 $\sqrt{2}$ ≈1.414， $\sqrt{20}$ ≈4.472，则 $\sqrt{0.2}$ ≈

查看试题解析
14. 如果点P (m+3，m－2)在x轴上，那么点P的坐标．

查看试题解析
15. 如图，工程队铺设一公路，他们从点A处铺设到点B处时，由于水塘挡路，他们决定改变方向经过点C，再拐到点D，然后沿着与AB平行的DE方向继续铺设，如果∠ABC＝120°，∠CDE＝140°，则∠BCD的度数是．

查看试题解析
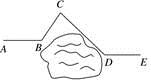16. 在平面直角坐标系中，以任意两点 P（x₁ ， y₁），Q（x₂ ， y₂）为端点的线段的中点坐标为 $(\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2})$ .现有 A（3，4），B（1，8），C（-2，6）三点，点D为线段AB的中点，点C 为线段AE的中点，则线段DE的中点坐标为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{16} - \sqrt[3]{64} \times \sqrt[3]{- 8}$ ；

(2)、 $| \sqrt{2} - 3 | + \sqrt{(- 3)^{2}} - (- 1)^{2019}$ .

查看试题解析
18. 求下列各式中x的值：

(1)、 ${(2 x + 7)}^{3} = - 27$

(2)、 ${(x - 2)}^{2} - 36 = 0$

查看试题解析
19. 如图，已知∠1=∠3，CD∥EF，试说明∠1=∠4.请将过程填写完整.
证明：∵∠1=∠3，
又∠2=∠3（    ），
∴∠1=  ▲   ，
∴  ▲  ∥  ▲  （    ），
又∵CD∥EF，
∴AB∥  ▲   ，
∴∠1=∠4（    ）.

查看试题解析
20. 已知a的立方根是2，b是 $\sqrt{13}$ 的整数部分，c是9的平方根，求a+b+c的算术平方根.

查看试题解析
21. 如图，点D、F在线段AB上，点E、G分别在线段BC和AC上， $C D ∥ E F$ ， $∠ 1 = ∠ 2$ .

(1)、求证： $D G ∥ B C$ ；

(2)、若DG是角 $∠ A D C$ 的平分线， $∠ 3 = 85 °$ ，且 $∠ D C E ： ∠ D C G = 9 ： 10$ ，请说明AB和CD怎样的位置关系？

查看试题解析
22. 如图，三角形ABC中任一点P（m，n）经平移后对应点为P₁（m+4，n-3），将三角形ABC作同样的平移得到三角形A₁B₁C₁ ．

(1)、直接写出A₁、C₁的坐标分别为A₁ ， C₁ ；

(2)、在图中画出△A₁B₁C₁；

(3)、求出△A₁B₁C₁的面积；

(4)、点M在y轴上，若三角形MOC₁的面积的面积为6，直接写出点M的坐标．

查看试题解析
23. 先阅读下列一段文字，再解答问题.已知在平面内有两点P₁（ $x_{1}$ ， $y_{1}$ ），P₂（ $x_{2}$ ， $y_{2}$ ），其两点间的距离公式为 $p_{1} p_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为 $| x_{2} - x_{1} |$ 或 $| y_{2} - y_{1} |$ .

(1)、已知点A（7，3），B（2， $- 9$ ），试求A，B两点间的距离；

(2)、已知点A，B在平行于 $x$ 轴的直线上，点A的横坐标为6，点B的横坐标为 $- 2$ ，试求A，B两点间的距离；

(3)、应用平面内两点间的距离公式，求代数式 $\sqrt{x^{2} + {(y + 1)}^{2}} + \sqrt{{(x + 6)}^{2} + {(y - 7)}^{2}}$ 的最小值.

查看试题解析
24. 如图所示，A(2，0)，点 B 在 y 轴上，将三角形 OAB 沿 x 轴负方向平移，平移后的图形为三角形 DEC，且点 C 的坐标为(-6，4) .

(1)、直接写出点 E 的坐标；

(2)、在四边形 ABCD 中，点 P 从点 B 出发，沿“BC→CD”移动.若点 P 的速度为每秒 2 个单位长度，运动时间为 t 秒，回答下列问题：
①求点 P 在运动过程中的坐标，(用含 t 的式子表示，写出过程)；

②当 3 秒＜t＜5 秒时，设∠CBP＝x°，∠PAD＝y°，∠BPA＝z°，试问 x，y，z 之间的数量关系能否确定？若能，请用含 x，y 的式子表示 z，写出过程；若不能，说明理由.

查看试题解析