浙江省台州市温岭团队八校2021-2022学年七年级下学期期中考试数学试题

试卷更新日期：2023-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 如右图，小手盖住的点的坐标可能是（）

A、（3， $-$ 4） B、（3，4） C、（ $-$ 3， $-$ 4） D、（ $-$ 3，4）

查看试题解析
2. 如图所示的车标，可以看作由平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 下列从左到右的变形中，正确的是（）

A、 $\sqrt[3]{- 5} = - \sqrt[3]{5}$ B、 $- \sqrt{3.6}$ =-0.6 C、 $\sqrt{{(- 10)}^{2}} = - 10$ D、 $\sqrt{81} = \pm 9$

查看试题解析
4. 在实数 $3.14 ， \sqrt[3]{8} ， 1.010010001 ⋯ ， \sqrt{5 ，} \frac{π}{3} ， \frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列命题中：①有公共顶点和一条公共边的两个角一定是邻补角；②垂直于同一条直线的两条直线互相垂直；③相等的角是对顶角；④经过直线外一点，有且只有一条直线与已知直线平行；其中真命题的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 如图， $A B$ $∥$ $C D$ ， $M P$ $∥$ $A B$ ， MN平分∠AMD，∠A=40°，∠D=30°，则∠NMP等于（）

A、15° B、10° C、7.5° D、5°

查看试题解析
7. 点P位于x轴下方，y轴左侧，距离x轴4个单位长度，距离y轴2个单位长度，那么点P的坐标是（）

A、 $(4 ， 2)$ B、 $(- 2 ， - 4)$ C、 $(- 4 ， - 2)$ D、 $(2 ， 4)$

查看试题解析
8. 如图，长方形ABCD位于第一象限，AB $∥$ $x$ 轴，AD $∥$ $y$ 轴.已知P（ $a$ ， $b$ ）是长方形ABCD（含边界）内的一个动点，A、C的坐标如图所示，则 $\frac{b}{a}$ 的最大值与最小值分别是（）

A、4， $\frac{1}{4}$ B、3， $\frac{1}{4}$ C、4， $\frac{1}{3}$ D、3， $\frac{1}{3}$

查看试题解析
9. 设 $(x]$ 表示小于 $x$ 的最大整数，如 $(3] = 2$ ， $(- 1.6] = - 2$ ，则下列结论中正确的是（）

A、 $(0] = 0$ B、 $x - (x]$ 的最小值是0 C、 $x - (x]$ 的最大值是1 D、不存在实数 $x$ ，使 $x - (x] = 0.2$

查看试题解析
10. 某同学去蛋糕店买面包，面包有A，B两种包装，每个面包品质相同，且只能整盒购买，商品信息如下：

A包装盒
B包装盒
每盒面包个数（个）
3
8
每盒价格（元）
5
11
若某同学正好买了50个面包，则他最少需要花（）元；

A、71 B、74 C、75 D、81

查看试题解析

二、填空题

11. 如图所示，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是．

查看试题解析
12. 已知 $\sqrt{2} \approx 1.414$ ，则 $\sqrt{0.02}$ = .

查看试题解析
13. 已知 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是方程 $2 x - a y = 8$ 的一个解，则 $a$ 的值是.

查看试题解析
14. 已知点A（3，2），AB∥x轴，且AB=4，则B点坐标为.

查看试题解析
15. 平方根节是数学爱好者的节日，这一天的月份和日期的数字正好是当年年份最后两位数字的平方根，例如2009年的3月3日。请你写出本世纪内你喜欢的一个平方根节（题中所举例子除外）：年月日.

查看试题解析
16. 如图，已知AB，CD，EF互相平行，且∠ABE＝70°，∠ECD＝150°，则∠BEC＝°.

查看试题解析
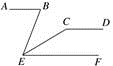17. 如图，一块直尺与缺了一角的等腰直角三角形如图摆放，若∠1=115°，则下列结论：①∠2=65°；②∠2=∠4；③∠2与∠3互余；④∠2+∠4=135°；其中正确的是（填序号）.

查看试题解析
18. 已知 $A_{1} (2 ， 1)$ ， $A_{2} (- 1 ， 0)$ ， …， $A_{k} (x_{k} ， y_{k})$ ， …，（k为正整数），且满足 $x_{k} = \frac{1}{1 - x_{k - 1}}$ ， $y_{k} = 1 - y_{k - 1}$ ，则A₂₀₂₂的坐标为.

查看试题解析

三、解答题

19. 计算 $\sqrt{16} + \sqrt[3]{- 27} + | 1 - \sqrt{3 |}$

查看试题解析
20. 解方程组：

(1)、 ${\begin{array}{l} x = 5 - y \\ 2 x - y = 4 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 5 y = 25 \\ 4 x + 3 y = 15 \end{array}$

查看试题解析
21. 如图，在平面直角坐标系中，已知点 $A (- 3 ， 3) ， B (- 5 ， 1) ， C (- 2 ， 0)$ ， $P (a ， b)$ 是 $△ A B C$ 的边 $A C$ 上任意一点， $△ A B C$ 经过平移后得到 $△ A_{1} B_{1} C_{1}$ ，点 $P$ 的对应点为 $P_{1} (a + 7 ， b - 3)$ .

(1)、在图中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积 $S$ .

查看试题解析
22. 已知：如图，GD $∥$ CA，∠1+∠2＝180°.

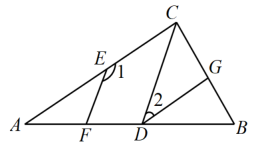(1)、试说明EF $∥$ CD成立的理由（完成下面填空）
证明：∵GD $∥$ CA
∴∠2＝  ▲  （              ）
又∵∠1+∠2＝180°（已知）
∴∠1+∠ECD＝  ▲  （              ）
∴EF $∥$ CD（              ）

(2)、若CD平分∠ACB，DG平分∠CDB，且∠A＝40°，求∠ACB的度数.

查看试题解析
23. 已知 $\sqrt[3]{389017}$ 为整数，为计算它的值，请你思考并回答下列问题.

(1)、整数1至9中，立方后，个位数字为7的是；

(2)、 $1 0^{3} = 1000$ ， $10 0^{3} = 1000000$ ，由此可知： $\sqrt[3]{389017}$ 是位数；

(3)、计算 $6 0^{3}$ ， $7 0^{3}$ ， $8 0^{3}$ ，再求 $\sqrt[3]{389017}$ 的值.

查看试题解析
24. 定理：任何两条夹在平行线间的垂线段长度相等.如图1，若直线a∥b，则有MN=PQ.运用此定理可得结论：如图2，直线a∥b，三角形ABC与三角形BCD，若都将BC看成底，则两三角形的高相等，从而面积相等，可记为S_三角形ABC=S_三角形BCD.
利用所得结论解决下列问题：

(1)、图2中，除S_三角形ABC=S_三角形BCD外，还有其它面积相等的三角形，请你写出所有面积相等的三角形；

(2)、如图3，已知三角形ABC，平面内有一点D，满足S_三角形ABC=S_三角形ABD，试画出所有符合题意的点D形成的图形（不要求写作法，作图工具不限）；

(3)、如图4，在一个8 $\times$ 8的网格中，我们把小正方形的顶点称为格点，每个小正方形的边长为1.若要在网格中找到格点C，使三角形ABC面积为2，则点C位置有几种可能.

查看试题解析
25. 有一条纸带ABCD，现小强对纸带进行了下列操作：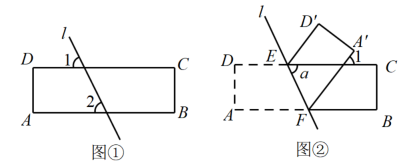

(1)、为了检验纸带的两条边线AB与CD是否平行，小强如图①所示画了直线 $l$ 后，量得∠1=∠2，则 $A B ∥ C D$ ，理由为；

(2)、将这条上下两边互相平行的纸带折叠，如图②所示，设∠1为70°，请求出∠ $α$ 的度数；

(3)、如图③，已知这是一条长方形纸带，点E在折线AD→DC上运动，点F是AB上的动点，连接EF将纸带沿着EF折叠，使点A的对应点 $A^{'}$ 落在DC上，若 $∠ C A^{'} F = x$ ，请用含x的代数式来表示 $∠ E A A^{'}$ 的度数为.（直接写出答案）

查看试题解析
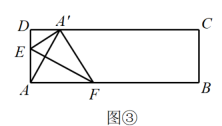26. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（ $a$ ， 0），B（ $b$ ， 0），C（-1，2），且 ${(a + 2)}^{2} + \sqrt{b - 4} = 0$ .

(1)、求 $a ， b$ 的值；

(2)、若点M在 $x$ 轴上运动，使三角形COM的面积是三角形ABC面积的2倍，请求出M的坐标；

(3)、过点C作AB的平行线，交y轴于点D，连接BD，过A作BD的平行线AE，交直线CD于点E，再作EG⊥ $x$ 轴于G.动点P从D出发，沿DE→EG方向运动，速度为每秒1个单位长度，设运动时间为t秒，请回答：
①求P在运动过程中的坐标（用含t的式子表示出来）；
②当6秒﹤t﹤8秒时，设∠EDP= $α$ ， ∠PBG= $β$ ， ∠DPB= $γ$ ，请求出 $α 、 β 、 γ$ 之间的数量关系.

查看试题解析

	A包装盒	B包装盒
每盒面包个数（个）	3	8
每盒价格（元）	5	11