福建省三明市四地四校2021-2022学年高二下学期数学期中联考试卷
试卷更新日期:2023-03-20 类型:期中考试
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 设命题 , 则的否定为( )A、 B、 C、 D、3. 已知命题 , 命题 , 则p是q的( )A、充分但不必要条件 B、必要但不充分条件 C、充分且必要条件 D、既不充分也不必要条件4. 已知函数 , 则的值为( )A、 B、-5 C、5 D、35. 已知函数的图象如图所示,则函数的图象可能是图中的( )
 A、
A、 B、
B、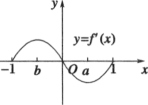 C、
C、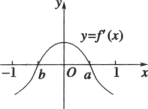 D、
D、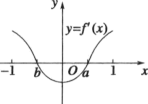 6. 甲、乙两人独立地去译一个密码,译出的概率分别、 , 现两人同时去译此密码,则该密码能被译出的概率是( )A、 B、 C、 D、7. 若正实数满足 , 则( )A、有最大值 B、有最大值4 C、有最小值 D、有最小值28. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图由四个全等的直角三角形和一个正方形构成.现用5种不同的颜色对这四个直角三角形和一个正方形区域涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
6. 甲、乙两人独立地去译一个密码,译出的概率分别、 , 现两人同时去译此密码,则该密码能被译出的概率是( )A、 B、 C、 D、7. 若正实数满足 , 则( )A、有最大值 B、有最大值4 C、有最小值 D、有最小值28. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图由四个全等的直角三角形和一个正方形构成.现用5种不同的颜色对这四个直角三角形和一个正方形区域涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( ) A、180 B、192 C、300 D、420
A、180 B、192 C、300 D、420二、多选题
-
9. 已知 , 则m可能的取值是( )A、0 B、1 C、2 D、310. 下列函数中,是同一函数的有( )A、 B、 C、 D、11. 若随机变量服从两点分布,其中 , 则下列结论正确的是( )A、 B、 C、 D、12. 4月23日为世界读书日,已知某高校学生每周阅读时间服从正态分布 , 则( )
(附: , , , . )
A、该校学生每周平均阅读时间为9小时; B、该校学生每周阅读时间的标准差为4; C、该校学生每周阅读时间不超过3小时的人数占0.15%; D、若该校有10000名学生,则每周阅读时间在3-5小时的人数约为210.三、填空题
-
13. 已知为奇函数,当时, , 则.14. 函数 的定义域为.15. 甲袋中有3个红球和2个白球,乙袋中有4个红球和1 个白球(除颜色外,球的大小、形状完全相同).先从甲袋中随机取出1球放入乙袋,再从乙袋中随机取出1球.分别以、表示由甲袋取出的球是红球和白球的事件,以表示由乙袋取出的球是红球的事件,则 , .16. 已知函数在区间上存在单调增区间,则m的取值范围为 .
四、解答题
-
17. 已知集合 , 集合 ,(1)、求;(2)、求 .18. 某班主任对本班40名同学每天参加课外活动的时间进行统计,并绘制成如图所示的频率分布直方图,其中[10,20),[20,30),[30,40),[40,50),[50,60)在纵轴上对应的高度分别为m,0.02,0.0375,0.0175,m.
 (1)、求实数m的值以及参加课外活动时间在[10,20)中的人数;(2)、从每天参加活动不少于50分钟的同学(含男生甲)中任选3人,求男生甲被选中的概率.19. 已知幂函数 为偶函数.(1)、求 的解析式;(2)、若函数 在区间 上的最大值为 ,求实数 的值.20. 已知5名同学站成一排,要求甲站在正中间,乙不站在两端,记满足条件的所有不同的排法种数为m.(1)、求m的值;(2)、求二项式的展开式中的常数项.21. 2022年2月20日,北京冬奥会在鸟巢落下帷幕,中国队创历史最佳战绩.北京冬奥会的成功举办推动了我国冰雪运动的普及,让越来越多的青少年爱上了冰雪运动.某校组织了一次全校冰雪运动知识竞赛,并抽取了100名参赛学生的成绩制作成如下频率分布表:
(1)、求实数m的值以及参加课外活动时间在[10,20)中的人数;(2)、从每天参加活动不少于50分钟的同学(含男生甲)中任选3人,求男生甲被选中的概率.19. 已知幂函数 为偶函数.(1)、求 的解析式;(2)、若函数 在区间 上的最大值为 ,求实数 的值.20. 已知5名同学站成一排,要求甲站在正中间,乙不站在两端,记满足条件的所有不同的排法种数为m.(1)、求m的值;(2)、求二项式的展开式中的常数项.21. 2022年2月20日,北京冬奥会在鸟巢落下帷幕,中国队创历史最佳战绩.北京冬奥会的成功举办推动了我国冰雪运动的普及,让越来越多的青少年爱上了冰雪运动.某校组织了一次全校冰雪运动知识竞赛,并抽取了100名参赛学生的成绩制作成如下频率分布表:竞赛得分
频率
(1)、如果规定竞赛得分在为“良好”,竞赛得分在为“优秀”,从成绩为“良好”和“优秀”的两组学生中,使用分层抽样抽取5人.现从这5人中抽取2人进行座谈,求两人竞赛得分都是“优秀”的概率;(2)、以这100名参赛学生中竞赛得分为“优秀”的频率作为全校知识竞赛中得分为“优秀”的学生被抽中的概率.现从该校学生中随机抽取3人,记竞赛得分为“优秀”的人数为 , 求随机变量的分布列及数学期望.22. 已知 .(1)、若曲线在点处的切线斜率为0,求的单调区间;(2)、若在上恒成立,求实数的取值范围.