福建省泉州市两校2021-2022学年高二下学期数学期中联考试卷
试卷更新日期:2023-03-20 类型:期中考试
一、单选题
-
1. 下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是 ( )
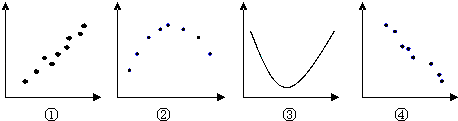 A、①③ B、①④ C、②③ D、①②2. 已知P(B|A)= ,P(A)= ,则P(AB)等于( )
A、①③ B、①④ C、②③ D、①②2. 已知P(B|A)= ,P(A)= ,则P(AB)等于( )
A、 B、 C、 D、3. 设等差数列 的前n项和为 ,若 ,则 ( )A、4 B、17 C、68 D、1364. 下列说法中正确的是( )A、已知随机变量服从二项分布 , 则 B、“与是互斥事件”是“与互为对立事件”的充分不必要条件 C、已知随机变量的方差为 , 则 D、已知随机变量的分布列为 , ,则=5. 已知函数 , 以下结论中错误的是( )A、是偶函数 B、有无数个零点 C、的最小值为 D、的最大值为6. 已知抛物线的焦点为 , 过点的直线交抛物线于 , 两点,延长交准线于点 , 若 , 则的值是( )A、 B、 C、 D、7. 莆田妈祖城有一钟楼,其顶部可视为正四棱柱与正四棱锥的组合体,如图,四个大钟分布在正四棱柱的四个侧面,则每天0点至12点(包含0点,不含12点)相邻两钟面上的时针成60°角的次数是( ) A、2 B、4 C、6 D、88. 已知 , 且 , 则( )A、 B、 C、 D、
A、2 B、4 C、6 D、88. 已知 , 且 , 则( )A、 B、 C、 D、二、多选题
-
9. 若的展开式中第3项与第8项的系数相等,则展开式中二项式系数最大的项为( )A、第4项 B、第5项 C、第6项 D、第7项10. 在网课期间,为了掌握学生们的学习状态,某省级示范学校对高二一段时间的教学成果进行测试.高二有1 000名学生,某学科的期中考试成绩(百分制且卷面成绩均为整数)Z服从正态分布 , 则(人数保留整数) ( )
参考数据:若 , .
A、年级平均成绩为82.5分 B、成绩在95分以上(含95分)人数和70分以下(含70分)人数相等 C、成绩不超过77分的人数少于150 D、超过98分的人数为111. “杨辉三角”是中国古代数学杰出的研究成果之一.如图所示,由杨辉三角的左腰上的各数出发,引一组平行线,从上往下每条线上各数之和依次为1,1,2,3,5,8,13, , 则下列选项正确的是( ) A、在第9条斜线上,各数之和为55 B、在第条斜线上,各数自左往右先增大后减小 C、在第条斜线上,共有个数 D、在第11条斜线上,最大的数是12. 已知椭圆的左、右焦点分别为、 , 长轴长为4,点在椭圆内部,点在椭圆上,则以下说法正确的是( )A、离心率的取值范围为 B、当离心率为时,的最大值为 C、存在点使得 D、的最小值为1
A、在第9条斜线上,各数之和为55 B、在第条斜线上,各数自左往右先增大后减小 C、在第条斜线上,共有个数 D、在第11条斜线上,最大的数是12. 已知椭圆的左、右焦点分别为、 , 长轴长为4,点在椭圆内部,点在椭圆上,则以下说法正确的是( )A、离心率的取值范围为 B、当离心率为时,的最大值为 C、存在点使得 D、的最小值为1三、填空题
-
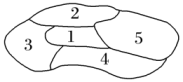
13. 的展开式中常数项是 .14. 已知 在 单调递减,则 的取值范围为 .15. 如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,共有5种颜色可供选择,则不同的着色方法共有种(以数字作答).
 16. 已知正方体的棱长为2,点E是棱的中点,点在平面内,若 , , 则的最小值为 .
16. 已知正方体的棱长为2,点E是棱的中点,点在平面内,若 , , 则的最小值为 .
四、解答题
-
17. 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:(1)、第1次抽到代数题且第2次抽到几何题的概率;(2)、在第1次抽到代数题的条件下,第2次抽到几何题的概率.18. 已知数列是等比数列,公比 , 且是的等差中项, .(1)、求数列的通项公式;(2)、若 , 求数列的前项和 .19. 如图所示的几何体中, , , 都是等腰直角三角形, , 且平面平面 , 平面平面 .
 (1)、求证:平面;(2)、求平面与平面夹角的余弦值.20. 2021年10月16日,神舟十三号载人飞船与天宫空间站组合体完成自主快速交会对接,航天员翟志刚、王亚平、叶光富顺利进驻天和核心舱,由此中国空间站开启了有人长期驻留的时代.为普及航天知识,某航天科技体验馆开展了一项“摸球过关”领取航天纪念品的游戏,规则如下:不透明的口袋中有3个红球,2个白球,这些球除颜色外完全相同.参与者每一轮从口袋中一次性取出3个球,将其中的红球个数记为该轮得分X,记录完得分后,将摸出的球全部放回袋中.当参与完成第n轮游戏,且其前n轮的累计得分恰好为2n时,游戏过关,可领取纪念品,同时游戏结束,否则继续参与游戏.若第3轮后仍未过关,则游戏也结束.每位参与者只能参加一次游戏.(1)、求随机变量X的分布列及数学期望;(2)、若甲参加该项游戏,求甲能够领到纪念品的概率.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值.20. 2021年10月16日,神舟十三号载人飞船与天宫空间站组合体完成自主快速交会对接,航天员翟志刚、王亚平、叶光富顺利进驻天和核心舱,由此中国空间站开启了有人长期驻留的时代.为普及航天知识,某航天科技体验馆开展了一项“摸球过关”领取航天纪念品的游戏,规则如下:不透明的口袋中有3个红球,2个白球,这些球除颜色外完全相同.参与者每一轮从口袋中一次性取出3个球,将其中的红球个数记为该轮得分X,记录完得分后,将摸出的球全部放回袋中.当参与完成第n轮游戏,且其前n轮的累计得分恰好为2n时,游戏过关,可领取纪念品,同时游戏结束,否则继续参与游戏.若第3轮后仍未过关,则游戏也结束.每位参与者只能参加一次游戏.(1)、求随机变量X的分布列及数学期望;(2)、若甲参加该项游戏,求甲能够领到纪念品的概率.