初中数学同步训练必刷题（北师大版七年级下册第四章三角形全章测试卷）

试卷更新日期：2023-03-18 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 三角形的两边长分别为 $4 c m$ 和 $7 c m$ ，此三角形第三边长可能是（）

A、 $2 c m$ B、 $3 c m$ C、 $6 c m$ D、 $11 c m$

查看试题解析
2. 如图， $△ A B C ≌ △ A D C$ ，若 $∠ B = 25 °$ ，则 $∠ D$ 的度数为（）

A、20° B、25° C、30° D、50°

查看试题解析
3. 如图的两个三角形是全等三角形，其中角和边的大小如图所示，那么∠1的度数是（）

A、 $43 °$ B、 $35 °$ C、 $55 °$ D、 $47 °$

查看试题解析
4. 如图是用尺规作 $∠ A O B$ 的平分线 $O C$ 的示意图，那么这样作图的依据是（）

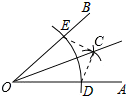A、SSS B、SAS C、ASA D、AAS

查看试题解析
5. 如图， $B C = B D$ ，那么添加下列选项中的一个条件后，仍无法判定 $△ A B C ≌ △ A B D$ 的是（）

A、 $A C = A D$ B、 $∠ B A C = ∠ B A D$ C、 $∠ A B C = ∠ A B D$ D、 $∠ C = ∠ D = 90 °$

查看试题解析
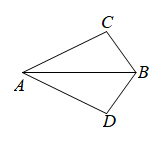6. 如图，将两块大小相同的三角板（∠B=∠C=30°的直角三角形）按图中所示的位置摆放.若BE交CF于点D交AC于点M，AB交CF于点N，则下列结论：①∠EAM=∠FAN；②△ACN≌△ABM；③∠EAF+∠BAC=120°；④EM=FN；⑤CF⊥BE中，正确的结论有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
7. 如图，点E、F在 $B C$ 上， $A B = C D$ ， $A F = D E$ ， $A F 、 D E$ 相交于点G，添加下列哪一个条件，可使得 $△ A B F ≌ △ D C E$ （）

A、 $∠ B = ∠ C$ B、 $A G = D G$ C、 $∠ A F E = ∠ D E F$ D、 $B E = C F$

查看试题解析
8. 如图是作△ABC的作图痕迹，则此作图的已知条件是（）

A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角

查看试题解析
9. 根据下列已知条件，能唯一画出△ABC的是（　　）

A、AB=3，BC=4，AC=8 B、∠C=90°，AB=6 C、AB=3，BC=3，∠C=30° D、∠A=60°，∠B=45°，AB=4

查看试题解析
10. 如图，为测量桃李湖两端AB的距离，南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C，测得∠ACB的度数，在AC的另一侧测得∠ACD=∠ACB，CD=CB，再测得AD的长，就是AB的长．那么判定△ABC≌△ADC的理由是（）

A、SAS B、SSS C、ASA D、AAS

查看试题解析

二、填空题（每空3分，共24分）

11. 若一个三角形三个内角的度数之比为1：2：3，则这个三角形是三角形(填“锐角”、“直角”或“钝角”) ．

查看试题解析
12. 如图，若 $△ A B C ≌ △ D E F$ ， $A C = 4$ ， $A B = 3$ ， $E F = 5$ ，则 $△ A B C$ 的周长为．

查看试题解析
13. 如图， $△ A B E ≌ △ A D C ≌ △ A B C$ ，若 $∠ 1 = 150 °$ ，则 $∠ α$ 的度数为．

查看试题解析
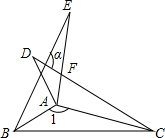14. 三个全等三角形摆成如图所示的形式，则 $∠ α + ∠ β + ∠ γ$ 的度数为.

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B = ∠ C$ ， D，E，F分别是边 $B C$ ， $A C$ ， $A B$ 上的点，且 $B F = C D$ ， $B D = C E$ ．若 $∠ A = 104 °$ ，则 $∠ E D F$ 的度数为°．

查看试题解析
16. 如图，点D，E分别在线段 $A B ， A C$ 上， $C D$ 与 $B E$ 相交于O点，已知 $A B = A C$ ，添加一个条件能直接用“ $A A S$ ”判定 $△ A B E ≌ △ A C D$ ，符合要求的条件是．

查看试题解析
17. 已知线段a ， b ， c ，求作△ABC ，使BC=a ， AC=b ， AB=c ，下面作法的合理顺序为 (填序号)①分别以B ， C为圆心，c ， b为半径作弧，两弧交于点A；②作直线BP ，在BP上截取BC=a；③连接AB ， AC ， △ABC为所求作的三角形。

查看试题解析
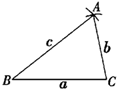18. 如图， $A C = D B$ ， $A O = D O$ ， $C D = 55 m$ ，则 $A$ 、 $B$ 两点之间的距离为 $m$ ．

查看试题解析

三、作图题（共2题，共15分）

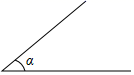
19. 已知：∠α．
求作：∠CAB，使得∠CAB＝∠α．

（尺规作图，保留作图痕迹，不写作法．）

查看试题解析
20. 小明站在池塘边的 $A$ 点处，池塘的对面（小明的正北方向） $B$ 处有一棵小树，他想知道这棵树距离他有多远，于是他向正东方向走了12步到达电线杆 $C$ 旁，接着再往前走了12步，到达 $D$ 处，然后他改向正南方向继续行走，当小明看到电线杆 $C$ 、小树 $B$ 与自己现处的位置 $E$ 在一条直线上时，他共走了60步.

(1)、根据题意，画出示意图（写出作图步骤）；

(2)、如果小明一步大约40 $c m$ ，估算出小明在点 $A$ 处时小树与他的距离为多少米，并说明理由.

查看试题解析

四、解答题（共6题，共51分）

21. 【实际问题】在拓展训练过程中，小明和组员为了完成测河宽的任务，在不能过河测量又没有任何测量工具的情况下，设计出下面的方案：小明面向河对岸的方向站好，然后调整帽子，使视线通过帽檐正好落在河对岸一点；然后，他转过身，保持刚才的姿态，这时视线通过帽檐落在了自己所在岸的某一点上；接着，他用步测的方法量出自己与那个点的距离，这个距离就是河的宽度．
【数学建模】将小明看成一条线段 $A B$ ，河对岸一点为点 $C$ ，自己所在岸的那个点为点 $D$ ，示意图如图所示，请你根据示意图帮助小明同学将问题补充完整，并解释其中的道理．
如图，如果 $A B ⊥ C D$ 于点 $A$ ， ▲ ，那么 $A C = A D$ ．
【问题解决】说明AC=AD的理由．

查看试题解析
22. 淇淇同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：如图 $A B ∥ O H ∥ C D$ ， AC与BD相交于点O，且 $O B = O D$ ．已知AB＝20米，请根据上述信息求标语CD的长度．

查看试题解析
23. 如图，点D在 $B C$ 上， $∠ A D B = ∠ B ， ∠ B A D = ∠ C A E$ .

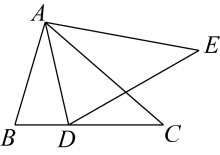(1)、添加条件：（只需写出一个），使 $△ A B C ≅ △ A D E$ ；

(2)、根据你添加的条件，写出证明过程.

查看试题解析
24. 如图所示，在 $△ A B C$ 中， $A D ⊥ B C$ 于D， $C E ⊥ A B$ 于E， $A D$ 与 $C E$ 交于点F，且 $A D = C D$ ．

(1)、 $△ A B D$ 与 $△ C F D$ 全等吗？请说明理由；

(2)、若 $B C = 9$ ， $A D = 7$ ，请求出AF的长．

查看试题解析
25. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = C B$ ，过点C作直线 $M N$ ， $A M ⊥ M N$ 于点M， $B N ⊥ M N$ 于点N．

(1)、若 $M N$ 在 $△ A B C$ 外（如图1），求证： $M N = A M + B N$ ；

(2)、若 $M N$ 与线段 $A B$ 相交（如图2），且 $A M = 2.6$ ， $B N = 1.1$ ，则 $M N =$ ．

查看试题解析
26. 如图，在五边形 $A B C D E$ 中， $A B = D E$ ， $A C = A D$ ．

(1)、请你添加一个条件，使得 $△ A B C ≌ △ D E A$ ，并说明理由；

(2)、在(1)的条件下，若 $∠ C A D = 66 °$ ， $∠ B = 110 °$ ，求 $∠ B A E$ 的度数．

查看试题解析

初中数学同步训练必刷题（北师大版七年级下册 第四章 三角形 全章测试卷）

一、单选题（每题3分，共30分）

二、填空题（每空3分，共24分）

三、作图题（共2题，共15分）

四、解答题（共6题，共51分）

初中数学同步训练必刷题（北师大版七年级下册第四章三角形全章测试卷）