初中数学同步训练必刷题(北师大版七年级下册4.1 认识三角形)
试卷更新日期:2023-03-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 某兴趣小组想用3根木棍组成一个三角形,3根木棍的长度不可能是( )A、2,3,4 B、3,4,5 C、2,5,7 D、4,7,72. 如图,是钝角三角形,以下是同学们作出的边上的高,其中作法正确的是( )A、
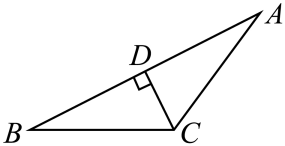 B、
B、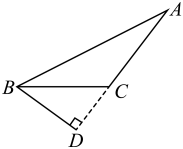 C、
C、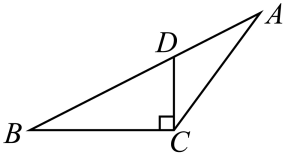 D、
D、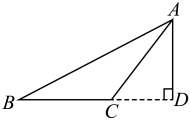 3. 长度为3,7,的三条线段构成三角形,则的值可能是( )A、3 B、4 C、8 D、124. 如图表示的是三角形的分类,则正确的表示是( )
3. 长度为3,7,的三条线段构成三角形,则的值可能是( )A、3 B、4 C、8 D、124. 如图表示的是三角形的分类,则正确的表示是( ) A、M表示三边均不相等的三角形,N表示等腰三角形,P表示等边三角形 B、M表示三边均不相等的三角形,N表示等边三角形,P表示等腰三角形 C、M表示等腰三角形,N表示等边三角形,P表示三边均不相等的三角形 D、M表示等边三角形,N表示等腰三角形,P表示三边均不相等的三角形5. 将一副三角板按如图所示放置,则下列结论:
A、M表示三边均不相等的三角形,N表示等腰三角形,P表示等边三角形 B、M表示三边均不相等的三角形,N表示等边三角形,P表示等腰三角形 C、M表示等腰三角形,N表示等边三角形,P表示三边均不相等的三角形 D、M表示等边三角形,N表示等腰三角形,P表示三边均不相等的三角形5. 将一副三角板按如图所示放置,则下列结论:①∠1=∠3;
②如果∠2=30°,则有AC∥DE;
③如果∠2=30°,则有BC∥AD;
④如果∠2=30°,必有∠4=∠C.其中正确的有( )
 A、①③ B、①②④ C、③④ D、①②③④6. 在△ABC中, , 则△ABC的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、形状无法确定7. 为估计池塘两岸间的距离,如图,小明在池塘一侧选取了一点 , 测得 , 那么之间的距离不可能是( )
A、①③ B、①②④ C、③④ D、①②③④6. 在△ABC中, , 则△ABC的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、形状无法确定7. 为估计池塘两岸间的距离,如图,小明在池塘一侧选取了一点 , 测得 , 那么之间的距离不可能是( ) A、5m B、15m C、20m D、30m8. 在中,如果 , 那么等于( )A、 B、 C、 D、9. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( )
A、5m B、15m C、20m D、30m8. 在中,如果 , 那么等于( )A、 B、 C、 D、9. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( ) A、 B、 C、 D、10. 如图:已知 , BD、CD、BE分别平分的内角、外角、外角 , 其中点D、C、E在同一条直线上,以下结论:错误的是( )
A、 B、 C、 D、10. 如图:已知 , BD、CD、BE分别平分的内角、外角、外角 , 其中点D、C、E在同一条直线上,以下结论:错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分, 共27分)
-
11. 在中,若 , , 则是三角形.(填“锐角”、“直角”、或“钝角”)12. 在中, , , 则°,°.13. 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=70°,∠C=40°,则∠DAE的度数为 .
 14. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .15. 如图,若 , 且于点C,若 , 则的度数为.
14. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .15. 如图,若 , 且于点C,若 , 则的度数为. 16. 如图,在中, , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.
16. 如图,在中, , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是. 17. 已知 AD、AE 分别是△ABC 的高和中线,若 BD=2,CD=1,则DE的长为 .18. 如图,AD是△ABC的中线,若AB=16,AC=10,则△ABD的周长与△ACD的周长的差为 .
17. 已知 AD、AE 分别是△ABC 的高和中线,若 BD=2,CD=1,则DE的长为 .18. 如图,AD是△ABC的中线,若AB=16,AC=10,则△ABD的周长与△ACD的周长的差为 .
三、解答题(共8题,共63分)
-
19. 如图,已知△ABC,请利用尺规作图法在AC上求作一点P,使得BP平分∠ABC.(保留作图痕迹,不写作法)
 20. 如图,在△ABC中,AD为∠BAC的角平分线,FE垂直平分AD,垂足为E,EF交BC的延长线于点F,若∠CAF=50°,求∠B的度数.
20. 如图,在△ABC中,AD为∠BAC的角平分线,FE垂直平分AD,垂足为E,EF交BC的延长线于点F,若∠CAF=50°,求∠B的度数. 21. 已知a、b、c为△ABC的三边长;
21. 已知a、b、c为△ABC的三边长;①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
22. 如图,在△ABC中,∠ABC=∠ACB=2∠A,BD是边AC上的高. (1)、依题意补全图形;(2)、求∠DBC的度数.23. 已知 为三角形三边的长, 化简: .24. 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
(1)、依题意补全图形;(2)、求∠DBC的度数.23. 已知 为三角形三边的长, 化简: .24. 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.