冲刺2023中考——数学模拟考场仿真演练卷六
试卷更新日期:2023-03-18 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 的绝对值是( )A、 B、 C、 D、2. 下列计算正确的是( )A、2ab﹣ab=ab B、2ab+ab=2a2b2 C、4a3b2﹣2a=2a2b D、﹣2ab2﹣a2b=﹣3a2b23. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
4. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )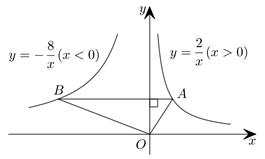 A、3 B、5 C、6 D、105. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A、3 B、5 C、6 D、105. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、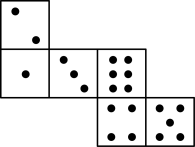 B、
B、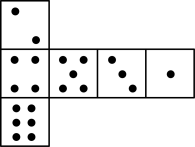 C、
C、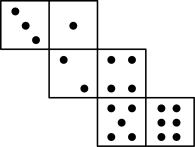 D、
D、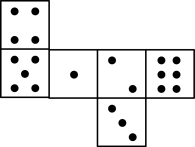 6. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
6. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )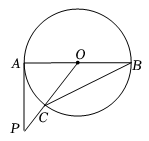 A、25° B、35° C、40° D、50°8. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
A、25° B、35° C、40° D、50°8. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )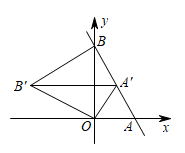 A、 B、 C、2 D、9. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( )
A、 B、 C、2 D、9. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( ) A、 B、2 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、 B、2 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每空3分,共18分)
-
11. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 .
 12. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .
12. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .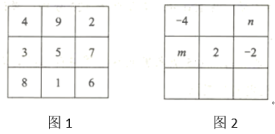 13. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
13. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )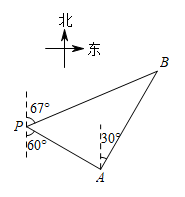 14. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
14. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .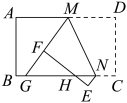 15. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
15. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).
 16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
三、解答题(共8题,共72分)
-
17.(1)、先化简再求值: , 其中m=4.(2)、解不等式组并将解集表示在所给的数轴上.
 18. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.
18. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.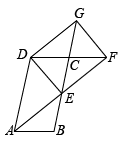 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.19. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.19. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.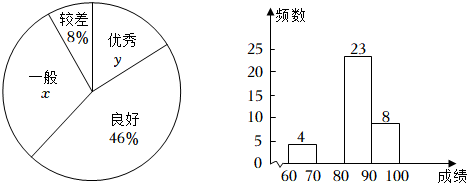
请根据统计图提供的信息,回答如下问题:
(1)、x= ▲ , y= ▲ , 并将直方图补充完整;(2)、已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是 , 众数是;(3)、若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;(4)、本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.20. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .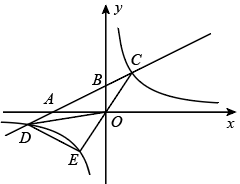 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.21. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)、我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.21. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)、我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)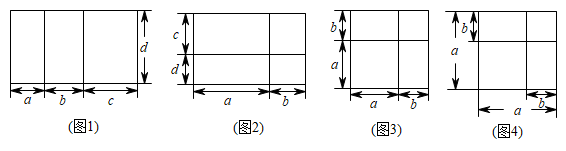
公式①:
公式②:
公式③:
公式④:
图1对应公式 , 图2对应公式 , 图3对应公式 , 图4对应公式;
(2)、《几何原本》中记载了一种利用几何图形证明平方差公式的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)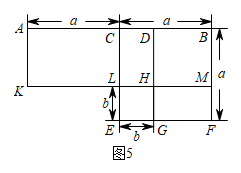 (3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.
(3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.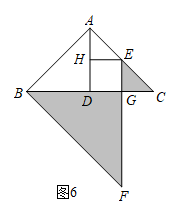
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
22. 如图是直径,A是上异于C,D的一点,点B是延长线上一点,连接、、 , 且 .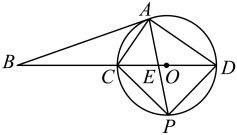 (1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.23. 如图,直线分别与x轴、y轴交于点A、B,点C为线段上一动点(不与A、B重合),以C为顶点作 , 射线交线段于点D,将射线绕点O顺时针旋转交射线于点E,连接.
(1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.23. 如图,直线分别与x轴、y轴交于点A、B,点C为线段上一动点(不与A、B重合),以C为顶点作 , 射线交线段于点D,将射线绕点O顺时针旋转交射线于点E,连接.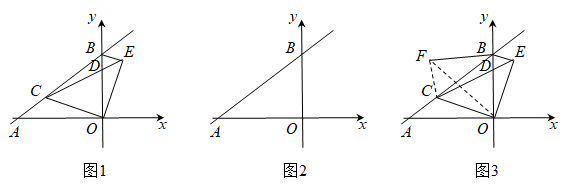 (1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)24. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)24. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.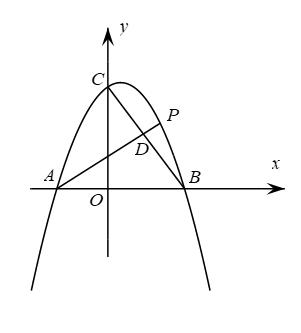 (1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,
(1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,①当与x轴平行时,求的值;
②当与x轴不平行时,求的最大值;
(3)、连接 , 是否存在点P,使得 , 若存在,求m的值,若不存在,请说明理由.