冲刺2023中考——数学模拟考场仿真演练卷五

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图是某几何体的三视图，该几何体是（）

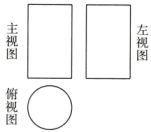A、圆柱 B、球 C、圆锥 D、正四棱柱

查看试题解析
2. 实数a、b在数轴.上的对应点位置如图所示，下列结论中正确的是（）

A、 $b > - 2$ B、 $| b | > a$ C、 $a + b > 0$ D、 $a - b < 0$

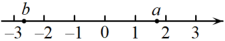查看试题解析
3. 如图，一条河两岸互相平行，为测得此河的宽度PT（PT与河岸PQ垂直），测P、Q两点距离为m米， $∠ P Q T = α$ ，则河宽PT的长度是（）

A、 $m s i n α$ B、 $m c o s α$ C、 $m t a n α$ D、 $\frac{m}{t a n α}$

查看试题解析
4. $1 - \sqrt{2}$ 的绝对值是（）

A、 $1 - \sqrt{2}$ B、 $\sqrt{2} - 1$ C、 $1 + \sqrt{2}$ D、 $\pm (\sqrt{2} - 1)$

查看试题解析
5. 下面四幅图是我国一些博物馆的标志，其中既是轴对称图形又是中心对称图形的是（）

A、温州博物馆 B、西藏博物馆 C、广东博物馆 D、湖北博物馆

查看试题解析
6. 如图， $a ∥ b$ ，将一个等腰直角三角板放置到如图所示位置．若 $∠ 1 = 15 °$ ，则 $∠ 2$ 的大小是（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $45 °$

查看试题解析
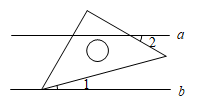7. 某校开展岗位体验劳动教育活动，设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位，每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动，则这两名同学恰好在同一岗位体验的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{1}{8}$ D、 $\frac{1}{16}$

查看试题解析
8. 甲、乙两人沿同一直道从 $A$ 地到 $B$ 地，在整个行程中，甲、乙离 $A$ 地的距离 $S$ 与时间 $t$ 之间的函数关系如图所示，下列说法错误的是（）

A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达，则甲用时10分钟 D、若甲出发时的速度为原来的2倍，则甲比乙提前1分钟到达 $B$ 地

查看试题解析
9. 如图，在▱ABCD中，AB＝8，点E是AB上一点，AE＝3，连接DE，过点C作CF∥DE，交AB的延长线于点F，则BF的长为（）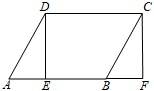

A、5 B、4 C、3 D、2

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的对称轴为直线 $x = 1$ ，抛物线与x轴的一个交点坐标为 $(- 1 ， 0)$ ），下列结论：① $a b c < 0$ ；② $3 a + c = 0$ ；③当 $y > 0$ 时，x的取值范围是 $- 1 ⩽ x < 3$ ；④点 $(- 2 ， y_{1})$ ， $(2 ， y_{2})$ 都在抛物线上，则有 $y_{1} < 0 < y_{2}$ ．其中结论正确的个数是（）

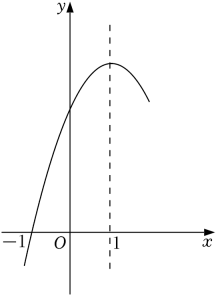A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空3分，共18分）

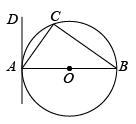
11. 已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m²﹣n²的值是．

查看试题解析
12. 关于x的不等式组 ${\begin{array}{l} - x + a < 2 \\ \frac{3 x - 1}{2} ⩽ x + 1 \end{array}$ 恰有3个整数解，则a的取值范围是.

查看试题解析
13. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
14. 如图， $△ A B C$ 内接于 $⊙ O ， A B$ 是直径，过点A作 $⊙ O$ 的切线 $A D$ ．若 $∠ B = 35 °$ ，则 $∠ D A C$ 的度数是度．

查看试题解析
15. 如图，反比例函数 $y = \frac{k}{x}$ 的图象经过矩形 $A B C D$ 对角线的交点E和点A，点B、C在x轴上， $△ O C E$ 的面积为6，则 $k =$ ．

查看试题解析
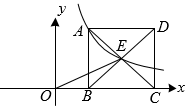16. 2021年5月7日，《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家，他是第一个将圆周率 $π$ 精确到小数点后第七位的人，他给出 $π$ 的两个分数形式： $\frac{22}{7}$ （约率）和 $\frac{355}{113}$ （密率）.同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数 $x$ 的不足近似值和过剩近似值分别为 $\frac{b}{a}$ 和 $\frac{d}{c}$ （即有 $\frac{b}{a} < x < \frac{d}{c}$ ，其中 $a$ ， $b$ ， $c$ ， $d$ 为正整数），则 $\frac{b + d}{a + c}$ 是 $x$ 的更为精确的近似值.例如：已知 $\frac{157}{50} < π < \frac{22}{7}$ ，则利用一次“调日法”后可得到 $π$ 的一个更为精确的近似分数为： $\frac{157 + 22}{50 + 7} = \frac{179}{57}$ ；由于 $\frac{179}{57} \approx 3.1404 < π$ ，再由 $\frac{179}{57} < π < \frac{22}{7}$ ，可以再次使用“调日法”得到 $π$ 的更为精确的近似分数……现已知 $\frac{7}{5} < \sqrt{2} < \frac{3}{2}$ ，则使用两次“调日法”可得到 $\sqrt{2}$ 的近似分数为.

查看试题解析

三、解答题（共8题，共72分）

17.

(1)、解不等式组 ${\begin{array}{l} x - 3 (x - 2) > 4 ① \\ \frac{2 x - 1}{3} \geq \frac{3 x + 2}{6} - 1 ② \end{array}$ ，并写出该不等式组的最小整数解．

(2)、先化简，再求值：（ $\frac{a^{2} - 9}{a^{2} - 6 a + 9}$ +1）÷ $\frac{a^{2}}{2 a - 6}$ ，其中a＝4sin30°﹣（π﹣3）⁰ ．

查看试题解析
18. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $B D$ 为 $⊙ O$ 的直径， $A C$ 平分 $∠ B A D ， C D = 2 \sqrt{2}$ ，点E在 $B C$ 的延长线上，连接 $D E$ ．

(1)、求直径 $B D$ 的长；

(2)、若 $B E = 5 \sqrt{2}$ ，计算图中阴影部分的面积．

查看试题解析
19. 某学校为满足学生多样化学习需求，准备组建美术、劳动、科普、阅读四类社团．学校为了解学生的参与度，随机抽取了部分学生进行调查，将调查结果绘制成如图所示的不完整的统计图．请根据图中的信息，解答下列问题：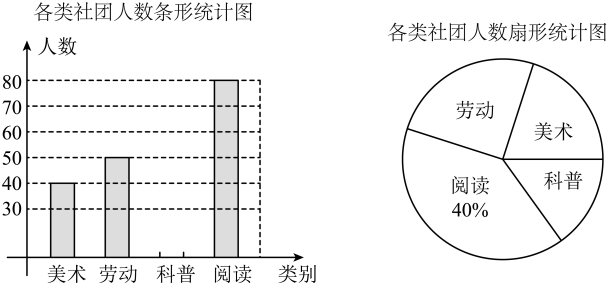

(1)、求本次调查的学生人数，并补全条形统计图；

(2)、若全校共有学生3600人，求愿意参加劳动类社团的学生人数；

(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团，请用树状图或列表法表示出所有等可能结果，并求出恰好选中同一社团的概率．

查看试题解析
20. 知识再现：如图1，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c．
∵ $s i n A = \frac{a}{c}$ ， $s i n B = \frac{b}{c}$

∴ $c = \frac{a}{s i n A}$ ， $c = \frac{b}{s i n B}$

∴ $\frac{a}{s i n A} = \frac{b}{s i n B}$

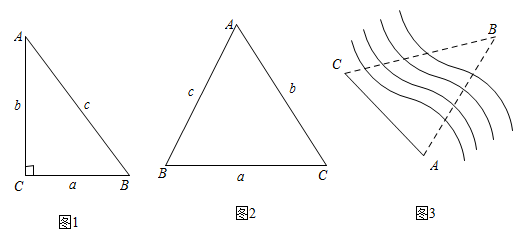(1)、拓展探究：如图2，在锐角ABC中，∠A，∠B，∠C的对边分别为a，b，c．请探究 $\frac{a}{s i n A}$ ， $\frac{b}{s i n B}$ ， $\frac{c}{s i n C}$ 之间的关系，并写出探究过程．

(2)、解决问题：如图3，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC＝60m，∠A＝75°，∠C＝60°．请用拓展探究中的结论，求点A到点B的距离．

查看试题解析
21. 如图，已知一次函数y＝ax+b与反比例函数y＝ $\frac{m}{x}$ （x＜0）的图像交于A（﹣2，4），B（﹣4，2）两点，且与x轴和y轴分别交于点C、点D．

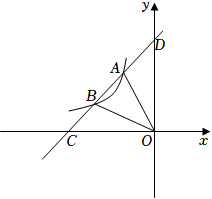(1)、根据图像直接写出不等式 $\frac{m}{x}$ ＜ax+b的解集；

(2)、求反比例函数与一次函数的解析式；

(3)、点P在y轴上，且S_△AOP＝ $\frac{1}{2}$ S_△AOB ，请求出点P的坐标．

查看试题解析
22. 如图，平行四边形 $A B C D$ 中， $A B = 5 ， B C = 10 ， B C$ 边上的高 $A M = 4$ ，点E为 $B C$ 边上的动点（不与B、C重合，过点E作直线 $A B$ 的垂线，垂足为F，连接 $D E 、 D F$ ．

(1)、求证： $△ A B M ∽ △ E B F$ ；

(2)、当点E为 $B C$ 的中点时，求 $D E$ 的长；

(3)、设 $B E = x ， △ D E F$ 的面积为y，求y与x之间的函数关系式，并求当x为何值时，y有最大值，最大值是多少？

查看试题解析
23. 已知，点 $E$ 、 $F$ 、 $G$ 、 $H$ 分别在正方形 $A B C D$ 的边 $A B$ 、 $B C$ 、 $C D$ 、 $A D$ 上．

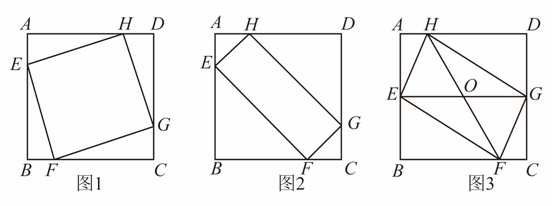(1)、如图1，当四边形 $E F G H$ 是正方形时，求证： $A E + A H = A B$ ；

(2)、如图2，已知 $A E = A H$ ， $C F = C G$ ，当 $A E$ 、 $C F$ 的大小有关系时，四边形 $E F G H$ 是矩形；

(3)、如图3， $A E = D G$ ， $E G$ 、 $F H$ 相交于点 $O$ ， $O E ： O F = 4 ： 5$ ，已知正方形 $A B C D$ 的边长为16， $F H$ 长为20，当 $△ O E H$ 的面积取最大值时，判断四边形 $E F G H$ 是怎样的四边形？证明你的结论．

查看试题解析
24. 如图，抛物线y＝ax²＋bx＋c交x轴于A(-1，0)，B两点，交y轴于点C(0，3)，顶点D的横坐标为1．

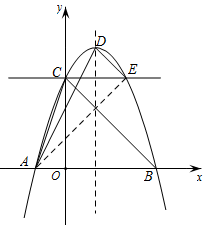(1)、求抛物线的解析式；

(2)、在y轴的负半轴上是否存在点P使∠APB＋∠ACB＝180°．若存在，求出点P的坐标，若不存在，请说明理由；

(3)、过点C作直线l与y轴垂直，与抛物线的另一个交点为E，连接AD，AE，DE，在直线l下方的抛物线上是否存在一点M，过点M作MF⊥l，垂足为F，使以M，F，E三点为顶点的三角形与ΔADE相似？若存在，请求出M点的坐标，若不存在，请说明理由．

查看试题解析