江西省南昌市2023年九年级下学期中考第一次学习效果检测数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( )
 A、相切 B、相交 C、相离 D、平行2. 下列函数中,满足y的值随x的值增大而减小的是( )A、 B、 C、 D、3. 公园中的休闲桌如图所示,下面为其俯视图的是( )
A、相切 B、相交 C、相离 D、平行2. 下列函数中,满足y的值随x的值增大而减小的是( )A、 B、 C、 D、3. 公园中的休闲桌如图所示,下面为其俯视图的是( ) A、
A、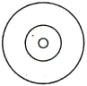 B、
B、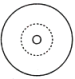 C、
C、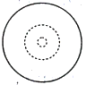 D、
D、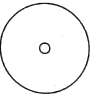 4. 某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
4. 某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( ) A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率; B、任意写一个整数,它能被2整除的概率; C、掷一枚质地均匀正六面体骰子,向上的面点数是2的概率 D、暗箱中有1个红球和2个白球,它们只有颜色上的区别,从中任取一球是白球的概率5. 某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流与电阻的关系图象,该图象经过点 . 根据图象可知,下列说法正确的是( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率; B、任意写一个整数,它能被2整除的概率; C、掷一枚质地均匀正六面体骰子,向上的面点数是2的概率 D、暗箱中有1个红球和2个白球,它们只有颜色上的区别,从中任取一球是白球的概率5. 某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流与电阻的关系图象,该图象经过点 . 根据图象可知,下列说法正确的是( ) A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是6. 如图,是抛物线 的图象,根据图象信息分析下列结论:① ;② ;③ ;④ .其中正确的结论是( )
A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是6. 如图,是抛物线 的图象,根据图象信息分析下列结论:① ;② ;③ ;④ .其中正确的结论是( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
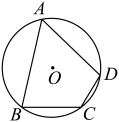
7. 如图,四边形为圆内接四边形,若 , 则 .
 8. 在中, , 则 .9. 如图是某高铁站扶梯的示意图,扶梯AB的坡度 . 李老师乘扶梯从底端A以的速度用时到达顶端B,则李老师上升的垂直高度为 .
8. 在中, , 则 .9. 如图是某高铁站扶梯的示意图,扶梯AB的坡度 . 李老师乘扶梯从底端A以的速度用时到达顶端B,则李老师上升的垂直高度为 . 10. 已知是方程的两个实数根,求的值为 .11. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中图形的周长为 .
10. 已知是方程的两个实数根,求的值为 .11. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中图形的周长为 .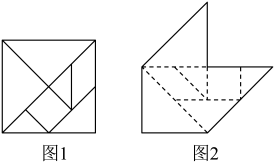 12. 已知点 , 的半径为1,OA切于点A,点P为上的动点,连接OP,AP,若是等腰三角形,则点P的坐标为 .
12. 已知点 , 的半径为1,OA切于点A,点P为上的动点,连接OP,AP,若是等腰三角形,则点P的坐标为 .
三、解答题
-
13.(1)、解方程: .(2)、为了测量校园内一棵树的高度,学校数学应用实践小组做了如下的探索实践.根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树的水平地面点E处,然后一同学沿着直线后退到点D,这时该同学恰好在镜子里看到树梢顶点A,再用皮尺量得 , 该同学身高 . 请你计算树()的高度.
 14. 如图1是一张折叠型方桌子,图2是其侧面结构示意图,支架与交于点O,测得 , .
14. 如图1是一张折叠型方桌子,图2是其侧面结构示意图,支架与交于点O,测得 , . (1)、若 , 求的长;(2)、将桌子放平后,要使距离地面的高为 , 求两条桌腿需叉开角度 .15. 已知四边形是正方形, , 请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法)
(1)、若 , 求的长;(2)、将桌子放平后,要使距离地面的高为 , 求两条桌腿需叉开角度 .15. 已知四边形是正方形, , 请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法)
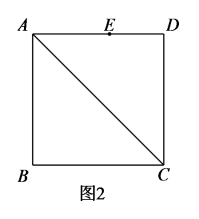 (1)、在图1中,将线段绕着点A顺时针旋转;(2)、在图2中,连接 , 将线段绕着点C顺时针旋转得到 .16. 如图,有一个质地均匀且四个面上分别标有数字“1”“2”“3”“4”的正四面体骰子,小明与小红按照以下规则进行游戏活动:两人轮流掷这枚骰子,骰子朝下的数字是几,就将棋子前进几格;开始棋子在数字“1”的那一格,小明先掷骰子,请解答下列问题:
(1)、在图1中,将线段绕着点A顺时针旋转;(2)、在图2中,连接 , 将线段绕着点C顺时针旋转得到 .16. 如图,有一个质地均匀且四个面上分别标有数字“1”“2”“3”“4”的正四面体骰子,小明与小红按照以下规则进行游戏活动:两人轮流掷这枚骰子,骰子朝下的数字是几,就将棋子前进几格;开始棋子在数字“1”的那一格,小明先掷骰子,请解答下列问题: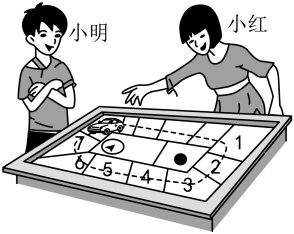 (1)、小明掷出骰子,数字“6”朝下的是____事件;A、不可能 B、必然 C、随机(2)、用列表或画树状图的方法求小红第一次掷完骰子后,棋子前进到数字“6”那一格的概率.17. 如图,在平面直角坐标系中,点A是y轴正半轴上一点,过点A作直线交反比例函数的图象于点B,E,过点A作轴,交反比例函数的图象于点C,连接 , .
(1)、小明掷出骰子,数字“6”朝下的是____事件;A、不可能 B、必然 C、随机(2)、用列表或画树状图的方法求小红第一次掷完骰子后,棋子前进到数字“6”那一格的概率.17. 如图,在平面直角坐标系中,点A是y轴正半轴上一点,过点A作直线交反比例函数的图象于点B,E,过点A作轴,交反比例函数的图象于点C,连接 , .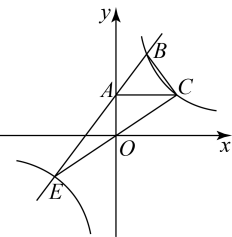 (1)、求反比例函数的表达式;(2)、求的面积.18. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为 , 主臂长为 , 测得主臂伸展角 .
(1)、求反比例函数的表达式;(2)、求的面积.18. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为 , 主臂长为 , 测得主臂伸展角 .(参考数据:)
 (1)、求点P到地面的高度;(2)、若挖掘机能挖的最远处点Q到点N的距离为 , 求的度数.19. 学校某数学调查小组通过随机调查了某社交App的6000名用户(男性4000人,女性2000人),从中随机抽取了60人(其中女性20人),统计他们在日常消费时是否使用手机支付的情况,定义:使用手机支付的为“手机支付族”,其他的为“非手机支付族”.根据抽样数据,绘制如下统计表.
(1)、求点P到地面的高度;(2)、若挖掘机能挖的最远处点Q到点N的距离为 , 求的度数.19. 学校某数学调查小组通过随机调查了某社交App的6000名用户(男性4000人,女性2000人),从中随机抽取了60人(其中女性20人),统计他们在日常消费时是否使用手机支付的情况,定义:使用手机支付的为“手机支付族”,其他的为“非手机支付族”.根据抽样数据,绘制如下统计表.手机支付族
非手机支付族
合计
男
30
10
40
女
a
8
20
合计
42
b
60
(1)、① ▲ , b ▲ ;②用样本估计总体,若从该社交App女性用户中随机抽取1位,这位女性用户是“手机支付族”的概率是多少?
(2)、某商场对“手机支付族”和“非手机支付族”有奖酬宾活动:凡购物满100元,均可得到一次抽奖的机会.在一个纸盒里装有2个红球和2个白球,它们除颜色外其他都相同,抽奖者一次从中摸出两个球,根据球的颜色决定赠送相应券值的礼金券.(如下表)手机支付族:
球
两红
一红一白
两白
礼金券/元
5
10
5
非手机支付族:
球
两红
一红一白
两白
礼金券/元
10
5
10
①用树状图表示某顾客进行一次摸奖的结果的所有情况;
②如果只考虑中奖因素,你将会选择哪种付费方式?请说明理由.
20. 点A是矩形边上的点,以为直径的圆交于点D和点C, , 连接 .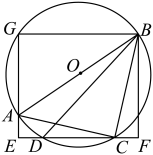 (1)、求证: .(2)、已知 , 求CD的长.21. 小黄做小商品的批发生意,其中某款“中国结”每件的成本为15元,该款“中国结”的批发单价y(元)与一次性批发量x(x为正整数)(件)之间满足如图所示的函数关系.
(1)、求证: .(2)、已知 , 求CD的长.21. 小黄做小商品的批发生意,其中某款“中国结”每件的成本为15元,该款“中国结”的批发单价y(元)与一次性批发量x(x为正整数)(件)之间满足如图所示的函数关系. (1)、当时,求y与x的函数关系式.(2)、某零售商在小黄处一次性批发该款“中国结”,共支付7280元,求此次批发量.(3)、某零售商在小黄处一次性批发该款“中国结”x()件,小黄获得的利润为w元,当x为何值时,小黄获得的利润最大?最大利润是多少元?22. 某公司为城市广场上一雕塑安装喷水装置.喷水口位于雕塑的顶端点B处,喷出的水柱轨迹呈现抛物线型.据此建立平面直角坐标系,如图.若喷出的水柱轨迹上某一点与支柱的水平距离为x(单位:m),与广场地面的垂直高度为y(单位:m).下面的表中记录了y与x的五组数据:
(1)、当时,求y与x的函数关系式.(2)、某零售商在小黄处一次性批发该款“中国结”,共支付7280元,求此次批发量.(3)、某零售商在小黄处一次性批发该款“中国结”x()件,小黄获得的利润为w元,当x为何值时,小黄获得的利润最大?最大利润是多少元?22. 某公司为城市广场上一雕塑安装喷水装置.喷水口位于雕塑的顶端点B处,喷出的水柱轨迹呈现抛物线型.据此建立平面直角坐标系,如图.若喷出的水柱轨迹上某一点与支柱的水平距离为x(单位:m),与广场地面的垂直高度为y(单位:m).下面的表中记录了y与x的五组数据:0
2
6
10
3
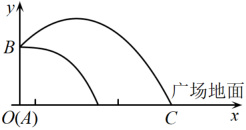
根据上述信息,解决以下问题:
(1)、求出与之间的函数关系;(2)、求水柱落地点与雕塑的水平距离;(3)、为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:在喷出水柱轨迹的形状不变的前提下,把水柱喷水的半径(动态喷水时,点C到AB的距离)控制在到之间,请探究改建后喷水池水柱的最大高度和b的取值范围.23. 如图,两个全等的四边形和 , 其中四边形的顶点O位于四边形的对角线交点O.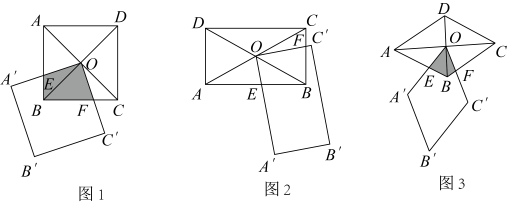 (1)、如图1,若四边形和都是正方形,则下列说法正确的有 . (填序号)
(1)、如图1,若四边形和都是正方形,则下列说法正确的有 . (填序号)①;②重叠部分的面积始终等于四边形的;③ .
(2)、应用提升:如图2,若四边形和都是矩形, , 写出与之间的数量关系,并证明.(3)、类比拓展:如图3,若四边形和都是菱形, , 判断(1)中的结论是否依然成立;如不成立,请写出你认为正确的结论(可用表示),并选取你所写结论中的一个说明理由.