河北省秦皇岛市2023年中考数学一模测试卷
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 经过直线 l 外一点O的四条直线中,与直线l相交的直线至少有( )
 A、1条 B、2条 C、3条 D、4条2. 下列四个数中,最小的数是( )A、0 B、3 C、 D、3. 如图,甲、乙、丙三个几何体均由四个大小相同的正方体组合而成,则下列说法错误的是( )
A、1条 B、2条 C、3条 D、4条2. 下列四个数中,最小的数是( )A、0 B、3 C、 D、3. 如图,甲、乙、丙三个几何体均由四个大小相同的正方体组合而成,则下列说法错误的是( ) A、甲与乙的主视图不同,左视图与俯视图都相同 B、甲与丙的主视图不相同,左视图与俯视图都不相同 C、甲与丙的主视图与俯视图相同,左视图不相同 D、甲、乙和丙的俯视图都相同4. 如果将一组数据中的每个数都减去2022,那么所得的一组新数据( )A、平均数不变 B、中位数不变 C、众数不变 D、方差不变5. 如图,已知与 , 分别以 , 为圆心,以同样长为半径画弧,分别交 , 于点 , , 交 , 于点 , . 以为圆心,以长为半径画弧,交弧于点H.下列结论错误的是( )
A、甲与乙的主视图不同,左视图与俯视图都相同 B、甲与丙的主视图不相同,左视图与俯视图都不相同 C、甲与丙的主视图与俯视图相同,左视图不相同 D、甲、乙和丙的俯视图都相同4. 如果将一组数据中的每个数都减去2022,那么所得的一组新数据( )A、平均数不变 B、中位数不变 C、众数不变 D、方差不变5. 如图,已知与 , 分别以 , 为圆心,以同样长为半径画弧,分别交 , 于点 , , 交 , 于点 , . 以为圆心,以长为半径画弧,交弧于点H.下列结论错误的是( ) A、 B、 C、 D、6. 如果单项式与是同类项,那么关于x的方程的解为( )A、 B、 C、 D、7. 若分式则在“”处的运算符号( )A、只能是“” B、可以是“”或“” C、不能是“” D、可以是“”或“”8. 如图,用四张同样大小的正方形纸片围出一个菱形 . 一个小孩顺次在这四张纸片上轮流走动,每一步都踩在一张纸片的中心,则这个小孩走的路线所围成的图形是( )
A、 B、 C、 D、6. 如果单项式与是同类项,那么关于x的方程的解为( )A、 B、 C、 D、7. 若分式则在“”处的运算符号( )A、只能是“” B、可以是“”或“” C、不能是“” D、可以是“”或“”8. 如图,用四张同样大小的正方形纸片围出一个菱形 . 一个小孩顺次在这四张纸片上轮流走动,每一步都踩在一张纸片的中心,则这个小孩走的路线所围成的图形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形9. 若x、y均为正整数,且 , 则的值为( )A、22 B、7 C、0 D、-1310. 如图,轮船在A处观测灯塔C位于北偏西方向上,轮船从A处以每小时40海里的速度沿南偏西方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西方向上,则下列说法正确的是( )
A、平行四边形 B、矩形 C、菱形 D、正方形9. 若x、y均为正整数,且 , 则的值为( )A、22 B、7 C、0 D、-1310. 如图,轮船在A处观测灯塔C位于北偏西方向上,轮船从A处以每小时40海里的速度沿南偏西方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西方向上,则下列说法正确的是( ) A、 B、点B到的距离为海里 C、海里 D、点B在点C的南偏东的方向上11. 如图,为的直径,C为圆上一点,为的内心,交于D,于 , 连接 , 则与的关系是( )
A、 B、点B到的距离为海里 C、海里 D、点B在点C的南偏东的方向上11. 如图,为的直径,C为圆上一点,为的内心,交于D,于 , 连接 , 则与的关系是( ) A、 B、 C、 D、12. 如图1,将一张长20cm,宽10cm的长方形硬纸片裁剪掉图中阴影部分之后,恰好折成如图2的有盖长方体纸盒,纸盒底面积为 , 则该有盖纸盒的高为( )
A、 B、 C、 D、12. 如图1,将一张长20cm,宽10cm的长方形硬纸片裁剪掉图中阴影部分之后,恰好折成如图2的有盖长方体纸盒,纸盒底面积为 , 则该有盖纸盒的高为( )
 A、4cm B、3cm C、2cm D、1cm13. 如图,在反比例函数的图象上有点 , 它们的纵坐标依次为6,2,1,分别过这些点作x轴与y轴的垂线段.图中阴影部分的面积记为 . 若 , 则的值为( )
A、4cm B、3cm C、2cm D、1cm13. 如图,在反比例函数的图象上有点 , 它们的纵坐标依次为6,2,1,分别过这些点作x轴与y轴的垂线段.图中阴影部分的面积记为 . 若 , 则的值为( ) A、3 B、4 C、5 D、614. “幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现将填入如图2所示的“幻方”中,部分数据已填入,则的值为( )
A、3 B、4 C、5 D、614. “幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现将填入如图2所示的“幻方”中,部分数据已填入,则的值为( )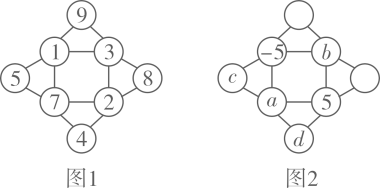 A、-50 B、 C、50 D、15. 定义一种运算:则函数的图象大致是( )A、
A、-50 B、 C、50 D、15. 定义一种运算:则函数的图象大致是( )A、 B、
B、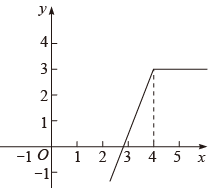 C、
C、 D、
D、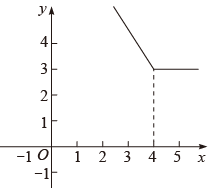 16. 如图,在中, , 点D为线段上一动点(不与点B,C重合),连接 , 作 , 交线段于点E.
16. 如图,在中, , 点D为线段上一动点(不与点B,C重合),连接 , 作 , 交线段于点E.下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若 , 则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
 A、只有甲同学符合题意 B、乙和丙同学都符合题意 C、甲和丙同学符合题意 D、三个同学都符合题意
A、只有甲同学符合题意 B、乙和丙同学都符合题意 C、甲和丙同学符合题意 D、三个同学都符合题意二、填空题
-
17. 若 , 则代数式的值为 .18. 如图,将一副直角三角板如图摆放, .
 (1)、与的位置关系是;(2)、在不标字母的情况下,找出与相等的角是 .19. 如图1,在 中, , , .动点 , 从点 同时出发,点 以每秒5个单位的速度沿边 向终点 匀速运动,点 以每秒6个单位的速度沿边 向终点 匀速运动,连接 ,以 为边作正方形 ,使得点 , 始终在 的同侧.设点 运动的时间为 秒.
(1)、与的位置关系是;(2)、在不标字母的情况下,找出与相等的角是 .19. 如图1,在 中, , , .动点 , 从点 同时出发,点 以每秒5个单位的速度沿边 向终点 匀速运动,点 以每秒6个单位的速度沿边 向终点 匀速运动,连接 ,以 为边作正方形 ,使得点 , 始终在 的同侧.设点 运动的时间为 秒. (1)、线段 的垂直平分线点 (填“经过”或“不经过”);(2)、 (用含 的式子表示);(3)、如图2,当点 落在边 上时, .
(1)、线段 的垂直平分线点 (填“经过”或“不经过”);(2)、 (用含 的式子表示);(3)、如图2,当点 落在边 上时, .三、解答题
-
20. 如图,数轴上的三个点A,B,C分别表示实数a,b,c.
 (1)、如果点C是的中点,那么a,b,c之间的数量关系是 ,(2)、比较与的大小,并说明理由;(3)、化简: .21. 为迎接七一建党节,某社区党委在广场上设计了一座三角形展台,需在它的每条边上摆放上相等盆数的鲜花进行装饰.若每条边上摆放两盆鲜花,共需要3盆鲜花;若每条边上摆放3盆鲜花,共需要6盆鲜花;……,按此要求摆放下去(如图所示,每个小圆圈表示一盆鲜花).
(1)、如果点C是的中点,那么a,b,c之间的数量关系是 ,(2)、比较与的大小,并说明理由;(3)、化简: .21. 为迎接七一建党节,某社区党委在广场上设计了一座三角形展台,需在它的每条边上摆放上相等盆数的鲜花进行装饰.若每条边上摆放两盆鲜花,共需要3盆鲜花;若每条边上摆放3盆鲜花,共需要6盆鲜花;……,按此要求摆放下去(如图所示,每个小圆圈表示一盆鲜花). (1)、填写下表:
(1)、填写下表:每条边上摆放的盆数(n)
2
3
4
5
6
…
需要的鲜花总盆数(y)
3
6
9
…
(2)、写出需要的鲜花总盆数y与n之间的关系式:(3)、能否用2023盆鲜花作出符合要求的摆放?如果能,请计算出每条边上应摆放的盆数;如果不能,请说明理由.22. 河北省某校为了增强学生的体质,引导同学们积极参加体育锻炼,学校购买了一批跳绳供学生借用,现从九年级随机抽取了部分学生对跳绳进行测试,并绘制了如下的两幅不完整的统计表和统计图.请根据相关信息,解答下列问题.一分钟跳绳成绩的频数统计表
组别
跳绳次数分段
频数
A
n
B
70
C
76
D
34
一分钟跳绳成绩的扇形统计图
 (1)、本次接受随机抽样调查的学生人数为多少人?统计表中的n的值是多少?扇形统计图中B组所对的圆心角是多少度?(2)、求抽取学生一分钟跳绳成绩的中位数所在的组别;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,请用画树状图或列表法求出恰好分组是一男一女的概率是多少?23. 如图,已知是等腰三角形, , 是锐角,点在边上,点在边上点、点不与所在线段端点重合 , , 连接 , , 射线AGBC,延长交射线于点 , 点在的延长线上,且 .
(1)、本次接受随机抽样调查的学生人数为多少人?统计表中的n的值是多少?扇形统计图中B组所对的圆心角是多少度?(2)、求抽取学生一分钟跳绳成绩的中位数所在的组别;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,请用画树状图或列表法求出恰好分组是一男一女的概率是多少?23. 如图,已知是等腰三角形, , 是锐角,点在边上,点在边上点、点不与所在线段端点重合 , , 连接 , , 射线AGBC,延长交射线于点 , 点在的延长线上,且 . (1)、与全等吗?请说明理由;(2)、请求出的度数.用含的代数式表示24. 某游泳馆推出了两种收费方式.
(1)、与全等吗?请说明理由;(2)、请求出的度数.用含的代数式表示24. 某游泳馆推出了两种收费方式.方式一:顾客先缴纳200元会员费,顾客本人一年内每次游泳再付费30元即可.
方式二:顾客不加入会员,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为(元),选择方式二的总费用为(元).
(1)、请分别写出 , 与x之间的函数表达式.(2)、小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.(3)、受疫情影响,有意向办年卡的会员由1800人减少到1600人,游泳馆打算更改会员制度,经调查发现,会员费每增加10元,减少40位顾客,游泳馆如何定价才能与以往的会员费收入持平?25. 如图1,已知矩形中, , , 点P是对角线的中点,点O为射线上的一个动点,连接 , 以为半径作 .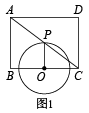
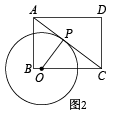
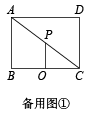
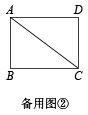 (1)、如图2,当与相切时,求的半径长;(2)、当点O运动到何处,的半径最小?(3)、在点O的运动过程中,与的三条边有四个交点,求的取值范围.26. 如图,抛物线L:与x轴交于点 , 两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为 .
(1)、如图2,当与相切时,求的半径长;(2)、当点O运动到何处,的半径最小?(3)、在点O的运动过程中,与的三条边有四个交点,求的取值范围.26. 如图,抛物线L:与x轴交于点 , 两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为 . (1)、求抛物线L和直线l的解析式;(2)、当点P在L上时,求m的值;(3)、过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.
(1)、求抛物线L和直线l的解析式;(2)、当点P在L上时,求m的值;(3)、过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.①当线段 , 求m的值;
②若P,M,N三点不重合,当其中两点关于第三点对称时,直接写出m的值.