广东省汕头市潮阳区2023年九年级数学一模试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 与 $\frac{1}{5}$ 互为倒数的数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、-5

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(2 a^{2})}^{3} = 6 a^{6}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $2 a - a = 2$

查看试题解析
3. 有一组数据：2，﹣2，2，4，6，7这组数据的中位数为（）

A、2 B、3 C、4 D、6

查看试题解析
4. 如图，AB＝AD，∠BAC＝∠DAC＝25°， $∠ D = 80 °$ ，则∠BCA的度数为（）

A、25° B、50° C、65° D、75°

查看试题解析
5. 下列说法正确的个数是（）
①0.01的立方根是0.000001；②如果一个角的两边分别平行于另一个角的两边，则两个角一定相等；③正三角形既是中心对称又是轴对称图形；④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形；⑤三角形的内心到三角形的三个顶点的距离相等

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 如图，在 $△ A B C$ 中，AB＝AC，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点.若BC＝4， $△ A B C$ 面积为10，则BM+MD长度的最小值为（）

A、 $\frac{5}{2}$ B、3 C、4 D、5

查看试题解析
7. 已知二次函数的解析式是y＝x²-2x-3，结合图象回答：当-2＜x＜2时，函数值y的取值范围是（）

A、-4≤y＜5 B、-4＜y＜5 C、-3≤y≤5 D、-4＜y＜-3

查看试题解析
8. 将反比例函数y＝ $\frac{4}{x}$ 的图象绕坐标原点O逆时针旋转30°，得到如图的新曲线A（-3，3 $\sqrt{3}$ ），B（ $\frac{3}{2} \sqrt{3}$ ， $\frac{3}{2}$ ）的直线相交于点C、D，则△OCD的面积为（）

A、3 B、8 C、2 $\sqrt{3}$ D、 $\frac{3}{2} \sqrt{3}$

查看试题解析
9. 对于实数 a，b，定义运算“#”如下：a#b＝a²－ab，如：3#2＝3²－3×2＝3，则方程（x＋1）#3＝2的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
10. 如图，正方形纸片ABCD，P为正方形AD边上的一点（不与点A，点D重合）.将正方形纸片折叠，使点B落在点P处，点C落在点G处，PG交DC于点H，折痕为EF，连接BP，BH，BH交EF于点M，连接PM.下列结论：①BE＝PE；②BP＝EF；③PB平分∠APG；④PH＝AP+HC；⑤MH＝MF，其中正确结论的个数是（　　）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. 因式分解： $4 x^{2} - 16$ =.

查看试题解析
12. 某商场的打折活动规定：凡在本商场购物，可转动转盘一次，并根据所转结果付账，其中不打折的概率为．

查看试题解析
13. 某楼梯的侧面如所述，测得 $A C = 4 m$ ， $∠ A C B = 30 °$ ，则该楼梯的高度 $A B =$ .

查看试题解析
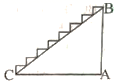14. 如图，一艘轮船以20海里/小时速度从南向北航行，当航行至A处时，测得小岛C在轮船的北偏东45度的方向处，航行一段时间后到达B处，此时测得小岛C在轮船的南偏东60度的方向处．若CB=40海里，则轮船航行的时间为．

查看试题解析
15.
如图，已知一次函数 $y = - x + 3 \sqrt{2}$ 的图象与坐标轴分别交于点A，B两点，⊙O的半径为1，P是线段AB上的一个点，过点P作⊙O的切线PQ，切点为Q，则PQ的最小值为．

查看试题解析

三、解答题

16. 计算：4cos30°-| $\sqrt{3}$ -2|+（ $\frac{\sqrt{5} - 1}{2}$ ）⁰- $\sqrt{27}$ +（- $\frac{1}{3}$ ）^-² ．

查看试题解析
17. 先化简 $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div (\frac{x - 1}{x + 1} - x + 1)$ ，然后从 $- 2$ ， $- 1$ ， 0，1选取一个合适的整数作为 $x$ 的值代入求值．

查看试题解析
18. 在某次数学测验中，一道题满分3分，老师评分只给整数，即得分只能为0分，1分，2分，3分，汤老师为了了解学生得分情况和试题的难易情况，对初三（1）班所有学生的试题进行了分析整理，并绘制了两幅尚不完整的统计图，如图所示．
小知识：难度系数的计算公式为： $L = \frac{X}{W}$ ，其中 $L$ 为难度系数， $X$ 为样本平均数， $W$ 为试题满分值．《考试说明》指出： $L$ 在0.7以上的题为容易题； $L$ 在 $0.4 ∼ 0.7$ 之间的题为中档题； $L$ 在 $0.2 ∼ 0.4$ 之间的题为较难题．
解答下列问题：

(1)、 $m =$ ▲ ， $n =$ ▲ ，并补全条形统计图；

(2)、在初三（1）班随机抽取一名学生的成绩，求抽中的成绩为2分的概率；

(3)、根据右侧“小知识”，通过计算判断这道题对于该班级来说，属于哪一类难度的试题？

查看试题解析
19. 如图，直角梯形 $A B C D$ 中， $A B / / C D$ ， $∠ A D C = 90 °$ ， $A B = A C$ ，过点B作 $B E ⊥ A C$ 于点E．

(1)、求证： $△ A D C ≌ △ B E A$ ；

(2)、若 $A D = 4 ， C D = 3$ ，求 $B C$ 的长．

查看试题解析
20. 某中学为丰富学生的校园生活，准备从友谊体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同、每个篮球的价格相同），若购买3个篮球和2个足球共需420元；购买2个篮球和4个足球共需440元．

(1)、购买一个篮球、一个足球各需多少元？

(2)、根据该中学的实际情况，需要从该体育用品商店一次性购买足球和篮球共20个．要求购买篮球数不少于足球数的2倍，总费用不超过1840元，那么这所中学有哪几种购买方案？哪种方案所需费用最少？

查看试题解析
21. 如图，在平面直角坐标系中，二次函数 y＝ax²+bx+c 的图象交 x 轴于A、B 两点，交 y 轴于 C 点，P 为 y 轴上的一个动点，已知 A（-2，0）、C（0，-2 $\sqrt{3}$ ），且抛物线的对称轴是直线 x＝1．

(1)、求此二次函数的解析式；

(2)、连接 PB，则 $\frac{1}{2}$ PC+PB 的最小值是；

(3)、连接 PA、PB，P 点运动到何处时，使得∠APB＝60°，请求出 P 点坐标．

查看试题解析
22. 问题发现：如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M，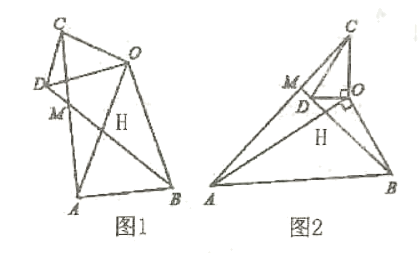

(1)、填空： $\frac{A C}{B D}$ 的值为； ∠AMB的度数为，

(2)、类比探究，如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M，请判断 $\frac{A C}{B D}$ 的值及∠AMB的度数，并说明理由：

查看试题解析