广东省河源市2023年九年级数学八校联考一模试卷

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 小明家购买了一款新型吹风机.如图所示，吹风机的主体是由一个空心圆柱体构成，手柄可近似看作一个圆柱体，这个几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
2. 在2020年新冠疫情期间，约42600人支援湖北，其中42600用科学记数法表示为（）

A、4.26×10³ B、4.26×10⁴ C、42.6×10³ D、0.426×10⁵

查看试题解析
3. 下列运算正确的是（）

A、 $m^{2} \cdot m^{4} = m^{8}$ B、 ${(- 2 m^{3})}^{2} = 4 m^{6}$ C、 $3 m + m^{2} = 3 a^{3}$ D、 $(m - n)^{2} = m^{2} - n^{2}$

查看试题解析
4. $x = 1$ 是关于 $x$ 的一元二次方程 $x^{2} + a x + 2 b = 0$ 的解，则 $2 a + 4 b =$ （）

A、-2 B、-3 C、4 D、-6

查看试题解析
5. 在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
6. 学校组织“超强大脑”答题赛，参赛的 11 名选手得分情况如表所示，那么这 11 名选手得分的中位数和众数分别是（）
分数（分）
60
80
90
95
人数（人）
2
2
3
4

A、86.5 和 90 B、80 和 90 C、90 和 95 D、90 和 90

查看试题解析
7. 如图，C，D是 $⊙ O$ 上直径 $A B$ 两侧的两点，设 $∠ A B C = 37 °$ ，则 $∠ B D C =$ （）

A、 $53 °$ B、 $63 °$ C、 $43 °$ D、 $74 °$

查看试题解析
8. 汽车产业的发展，有效促进了我国现代化建设．某汽车销售公司2018年盈利1000万元，2020年盈利1440万元，且从2018年到2020年，每年盈利的年增长率相同．设每年盈利的年增长率为x，则列方程得（）

A、1000（1+2x）＝1440 B、1000（1+x）²＝1440 C、1000×2×（1+x）＝1440 D、1000+1000（1+x）+1000（1+x）²＝1440

查看试题解析
9. 如果关于x的不等式组 ${\begin{array}{l} \frac{x - m}{2} \geq 0 \\ x + 3 < 3 (x - 1) \end{array}$ 的解集为 $x > 3$ ，且关于x的分式方程 $\frac{1 - x}{2 - x} + \frac{m}{x - 2} = 3$ 有非负数解，则符合条件的整数m的值的和是（）

A、0 B、-4 C、-5 D、-8

查看试题解析
10. 如图，正方形纸片ABCD，P为正方形AD边上的一点（不与点A，点D重合）.将正方形纸片折叠，使点B落在点P处，点C落在点G处，PG交DC于点H，折痕为EF，连接BP，BH，BH交EF于点M，连接PM.下列结论：①BE＝PE；②BP＝EF；③PB平分∠APG；④PH＝AP+HC；⑤MH＝MF，其中正确结论的个数是（　　）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. 因式分解： $4 x^{2} - 16$ =.

查看试题解析
12. 现有四张正面分别标有数字-3，-2，1，2的不透明卡片，它们除数字外其余完全相同，将他们背面朝上洗均匀后，随机抽取两张，记上面的数字分别为m，n，则使得一次函数 $y = 2 x + m + n$ 的图象不经过第二象限的概率为．

查看试题解析
13. 如图， $A B ＝ A C ＝ A D$ ，若 $A D ∥ B C$ ， $∠ C ＝ 70 °$ ，则 $∠ D$ ＝度．

查看试题解析
14. 若二次函数y=2x²的图象向左平移2个单位长度后，得到函数y=2（x+h）²的图象，则h= ．

查看试题解析
15. 如图， $△ A B C$ 与 $△ A E D$ 都是等腰三角形， $∠ A B C = ∠ A E D = 120 °$ ，点P为 $A C$ 边上一点，且 $P A = m$ ， $P B$ 与 $B A$ 所夹锐角为 $∠ P B A = β$ ，点E为 $P B$ 上一动点，求点E自点B运动至点P时，点D所经过的路径长．（用含β与m的式子表示）

查看试题解析

三、解答题

16. 计算： $(4 - \sqrt{3})^{0} - 3 t a n 60 ° - (- \frac{1}{2})^{- 1} + \sqrt{2}$ ．

查看试题解析
17. 先化简，再求值： $(\frac{2 x}{x^{2} - 4} - \frac{1}{x + 2}) \div \frac{x - 1}{x - 2}$ ，其中 x＝ $\sqrt{3} + 1$

查看试题解析
18. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况，在全校范围内随机抽查部分学生，对他们喜爱的体育项目（每人只选一项）进行了问卷调查，将统计数据绘制成如图两幅不完整统计图，请根据图中提供的信息解答下列各题．

(1)、 $m =$ ▲ $%$ ，这次共抽取了 ▲ 名学生进行调查；并补全条形图；

(2)、请你估计该校约有名学生喜爱打篮球；

(3)、现学校准备从喜欢跳绳活动的4人（三男一女）中随机选取2人进行体能测试，请利用列表或画树状图的方法，求抽到一男一女学生的概率是多少？

查看试题解析
19.
如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF= $\frac{1}{2}$ ∠CAB．

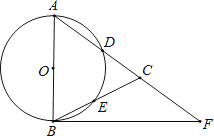(1)、求证：直线BF是⊙O的切线；

(2)、若AB=5，sin∠CBF= $\frac{\sqrt{5}}{5}$ ，求BC和BF的长．

查看试题解析
20. 开学前夕，某书店计划购进 A、B 两种笔记本共 350 本．已知 A 种笔记本的进价为 12 元/本，B 种笔记本的进价为 15 元/本，共计 4800 元．

(1)、请问购进了A种笔记本多少本？

(2)、在销售过程中，A、B两种笔记本的标价分别为20元/本、25元/本．受疫情影响，两种笔记本按标价各卖出m本以后，该店进行促销活动，剩余的A种笔记本按标价的七折全部售出，剩余的B种笔记本按成本价清货，若两种笔记本的总利润不少于2348元，请求出m的最小值．

查看试题解析
21. 如图，直线y=ax+1与x轴、y轴分别相交于A、B两点，与双曲线y= $\frac{k}{x}$ （x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（-2，0）．

(1)、求直线AP和双曲线的表达式；

(2)、若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．

查看试题解析
22. 某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：

(1)、【问题背景】如图1，正方形ABCD中，点E为AB边上一点，连接DE，过点E作EF⊥DE交BC边于点F，将△ADE沿直线DE折叠后，点A落在点 $A^{'}$ 处，当∠BEF＝25°，则∠FE $A^{'}$ ＝°．

(2)、【特例探究】如图2，连接DF，当点 $A^{'}$ 恰好落在DF上时，求证：AE＝2 $A^{'}$ F．

(3)、【深入探究】若把正方形ABCD改成矩形ABCD，且AD＝mAB，其他条件不变，他们发现AE与 $A^{'}$ F之间也存在着一定的数量关系，请直接写出AE与 $A^{'}$ F之间的数量关系式．

(4)、【拓展探究】若把正方形ABCD改成菱形ABCD，且∠B＝60°，∠DEF＝120°，其他条件不变，他们发现AE与 $A^{'}$ F之间也存在着一定的数量关系，请直接写出AE与A′F之间的数量关系式．

查看试题解析

分数（分）	60	80	90	95
人数（人）	2	2	3	4