安徽省合肥市长丰县2023年九年级一检数学试卷
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 下列四个数中,比-1小的数是( )A、 B、0 C、 D、-32. 今年春节黄金周安徽市场运行平衡,消费火热,从省商务厅获悉,春节假期,全省重点监测的254家零售和餐饮企业实现销售额26.15亿元、同比增长4.57%.数据26.15亿用科学记数法表示为( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图所示的几何体的主视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、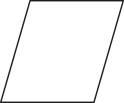 5. 下表记录了甲、乙、丙、丁四名运动员最近几次百米赛跑选拔赛成绩的平均数与方差:
5. 下表记录了甲、乙、丙、丁四名运动员最近几次百米赛跑选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数/秒
11.5
11
11.5
11
方差
2.6
2.6
6.3
5.4
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加市运动会,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 直线BD∥EF,两个直角三角板如图摆放,若∠CBD=10°,则∠1=( )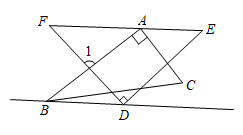 A、75° B、80° C、85° D、95°7. 若 , 是方程的两个实数根,则的值是( )A、5 B、-5 C、1 D、-18. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )
A、75° B、80° C、85° D、95°7. 若 , 是方程的两个实数根,则的值是( )A、5 B、-5 C、1 D、-18. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )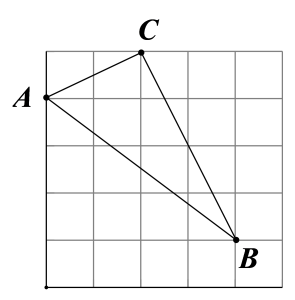 A、 B、 C、 D、9. 在同一平面直角坐标系中,反比例函数与二次函数的图象可能是( )A、
A、 B、 C、 D、9. 在同一平面直角坐标系中,反比例函数与二次函数的图象可能是( )A、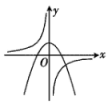 B、
B、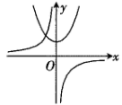 C、
C、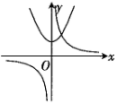 D、
D、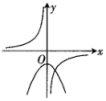 10. 如图,在中, , , 是下方的一动点,记 , 的面积分别记为 , . 若 , 则线段长的最小值是( )
10. 如图,在中, , , 是下方的一动点,记 , 的面积分别记为 , . 若 , 则线段长的最小值是( )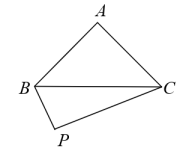 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. 不等式的解集为 .12. 除夕的早上,小瑞和弟弟准备以掷骰子的方式决定谁来贴春联,由小瑞来投掷1个骰子,若掷出的点数不是3的倍数,则小瑞贴春联,否则弟弟贴春联,则小瑞贴春联的概率为 .13. 如图,点 , , , 在半径为的上,连接 , , , . 若 , 则劣弧的长为 .
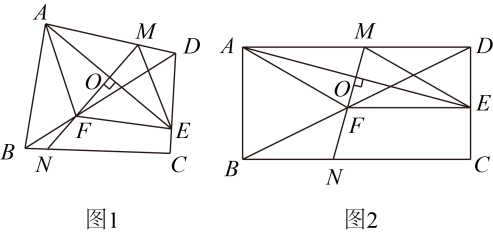
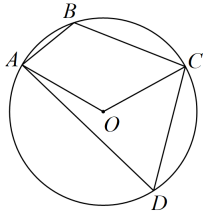 14. 如图,在正方形中,点 , 分别在边 , 上,且 , 交于点 , 交于点 , 的延长线交的延长线于点 , 且 , 连接 .
14. 如图,在正方形中,点 , 分别在边 , 上,且 , 交于点 , 交于点 , 的延长线交的延长线于点 , 且 , 连接 .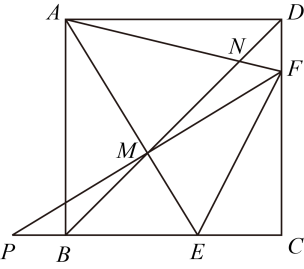 (1)、 .(2)、若 , , 则 .
(1)、 .(2)、若 , , 则 .三、解答题
-
15. 化简: .16. △OAB在平面直角坐标系中的位置如图所示.
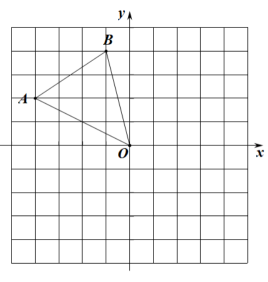
⑴画出与△OAB关于x轴对称的 . (其中与A对称,与B对称)
⑵将△OAB绕着点O顺时针方向旋转90°得到 , 画出 .
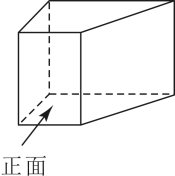
17. 如图,一次函数与反比例函数的图像交于、两点.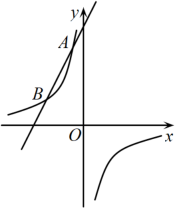 (1)、求一次函数与反比例函数的解析式.(2)、根据图像,请直接写出一次函数值大于反比例函数值时的取值范围.18. 观察下列等式的规律,解答下列问题:
(1)、求一次函数与反比例函数的解析式.(2)、根据图像,请直接写出一次函数值大于反比例函数值时的取值范围.18. 观察下列等式的规律,解答下列问题:第1个等式: .
第2个等式:
第3个等式: .
第4个等式: .
……
(1)、请你写出第5个等式: .(2)、写出你猜想的第个等式(用含的式子表示),并证明.19. 如图,为的直径,为的延长线上一点,过点作的切线,切点为点 , 连接、 , 过点作交延长线于点 . (1)、求证: .(2)、若 , , 求的长.20. 除夕夜,小马吃完年夜饭后沿着东西方向的街道散步,如图,当小马走到点处时发现处有一钟楼,此时观察到钟楼大约在小马的北偏西方向,小马继续向前走600米,走到处时观察到钟楼大约在小马的北偏西方向,求钟楼离街道的距离.(结果取整数,参考数据: , , , )
(1)、求证: .(2)、若 , , 求的长.20. 除夕夜,小马吃完年夜饭后沿着东西方向的街道散步,如图,当小马走到点处时发现处有一钟楼,此时观察到钟楼大约在小马的北偏西方向,小马继续向前走600米,走到处时观察到钟楼大约在小马的北偏西方向,求钟楼离街道的距离.(结果取整数,参考数据: , , , )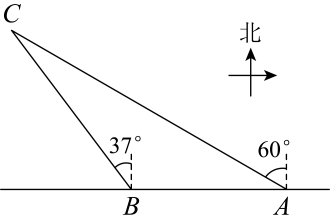 21. 第22届国际足联世界杯于2022年11月20日在卡塔尔境内举行,某校数学兴趣小组为了解该校同学对卡塔尔世界杯的关注程度,进行了问卷调查,并从中随机抽取份问卷,将调查结果分为四类:非常关注;比较关注;偶然关注;不感兴趣.将调查结果绘制成如图所示的不完整的统计图.请根据题中信息,完成下列问题:
21. 第22届国际足联世界杯于2022年11月20日在卡塔尔境内举行,某校数学兴趣小组为了解该校同学对卡塔尔世界杯的关注程度,进行了问卷调查,并从中随机抽取份问卷,将调查结果分为四类:非常关注;比较关注;偶然关注;不感兴趣.将调查结果绘制成如图所示的不完整的统计图.请根据题中信息,完成下列问题: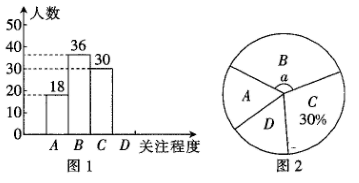 (1)、n= , a= .(2)、补全条形统计图.(3)、若本校有3000名同学,请估计该校对卡塔尔世界杯“非常关注”的人数.
(1)、n= , a= .(2)、补全条形统计图.(3)、若本校有3000名同学,请估计该校对卡塔尔世界杯“非常关注”的人数.