内蒙古呼伦贝尔市海拉尔区2022年中考适应性考试数学试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
1. 在实数0, , ,-3中,最小的是( )A、0 B、 C、 D、-32. 下列运算正确的是( )A、 B、 C、 D、3. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 且 C、 且 D、4. 对于一组数据1,1,3,1,4,下列结论错误的是( )A、平均数是2 B、众数是1 C、中位数是3 D、方差是1.65. 据光明日报网,中国科学技术大学的潘建伟、陆朝阳等人构建了一台76个光子100个模式的量子计算机“九章”.它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一百万亿倍.也就是说,超级计算机需要一亿年完成的任务,“九章”只需一分钟.其中一百万亿用科学记数法表示为( )A、 B、 C、 D、6. 一块含 角的直角三角板和直尺如图放置,若 ,则 的度数为( )
 A、 B、 C、 D、7. 若正多边形的一个内角是 ,则这个正多边形的边数为( )A、12 B、13 C、14 D、158. 下列命题正确的是( )A、圆心角的度数等于圆周角的度数的2倍 B、有两边相等的平行四边形是菱形 C、若 , ,且 ,则 有最大值2 D、若 ,则抛物线 与x轴没有交点9. 设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )A、有最大值 π B、有最小值 π C、有最大值 π D、有最小值 π10. 如图,在平面直角坐标系中,直线 分别交x轴,y轴于点A,点B,线段AB上有一点C,点C的横坐标为 ,过点C的直线 与直线AB垂直,交y轴于点D,则不等式 的所有负整数解的和是( )
A、 B、 C、 D、7. 若正多边形的一个内角是 ,则这个正多边形的边数为( )A、12 B、13 C、14 D、158. 下列命题正确的是( )A、圆心角的度数等于圆周角的度数的2倍 B、有两边相等的平行四边形是菱形 C、若 , ,且 ,则 有最大值2 D、若 ,则抛物线 与x轴没有交点9. 设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )A、有最大值 π B、有最小值 π C、有最大值 π D、有最小值 π10. 如图,在平面直角坐标系中,直线 分别交x轴,y轴于点A,点B,线段AB上有一点C,点C的横坐标为 ,过点C的直线 与直线AB垂直,交y轴于点D,则不等式 的所有负整数解的和是( )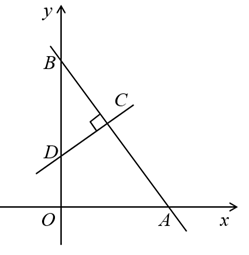 A、-10 B、-6 C、-3 D、-111. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
A、-10 B、-6 C、-3 D、-111. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( ) A、 B、 C、 D、12. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( )
A、 B、 C、 D、12. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、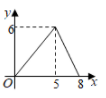 B、
B、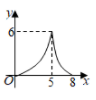 C、
C、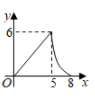 D、
D、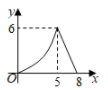
二、填空题
-
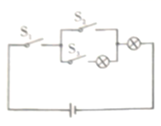
13. 在实数范围内分解因式: .14. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .
 15. 如图,在矩形纸片中, , , M是上的点,且 , 将矩形纸片沿过点M的直线折叠,使点D落在上的点P处,点C落在点处,折痕为 , 则线段的长是 .
15. 如图,在矩形纸片中, , , M是上的点,且 , 将矩形纸片沿过点M的直线折叠,使点D落在上的点P处,点C落在点处,折痕为 , 则线段的长是 .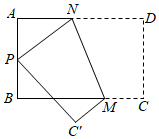 16. 已知点A为直线上一点,过点A作轴,交双曲线于点B.若点A与点B关于y轴对称,则点A的坐标为 .17. 如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在轴x正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2025次旋转后,顶点D的坐标为 .
16. 已知点A为直线上一点,过点A作轴,交双曲线于点B.若点A与点B关于y轴对称,则点A的坐标为 .17. 如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在轴x正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2025次旋转后,顶点D的坐标为 .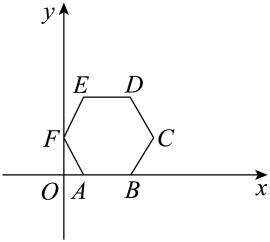
三、解答题
-
18. 计算: .19. 先化简,再求值:
,其中x满足 .
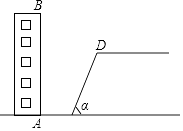
20. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O, .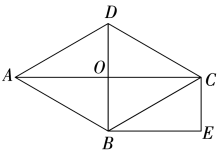 (1)、求证:四边形OBEC是矩形;(2)、若∠ABC=120°,AB=6,求矩形OBEC的周长;21. 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(1)、求证:四边形OBEC是矩形;(2)、若∠ABC=120°,AB=6,求矩形OBEC的周长;21. 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, ≈1.41, ≈1.73, ≈2.24)
 22. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
22. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;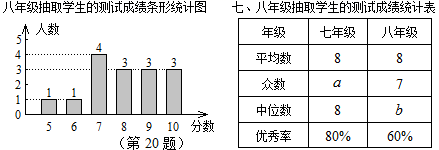 (1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.23. 公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s) 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.23. 公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s) 的关系分别可以用二次函数和一次函数表示,其图象如图所示. (1)、当甲车减速至9m/s时,它行驶的路程是多少?(2)、若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?24. 如图1,正方形ABCD的边长为4,点P在边BC上,⊙O经过A,B,P三点.
(1)、当甲车减速至9m/s时,它行驶的路程是多少?(2)、若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?24. 如图1,正方形ABCD的边长为4,点P在边BC上,⊙O经过A,B,P三点.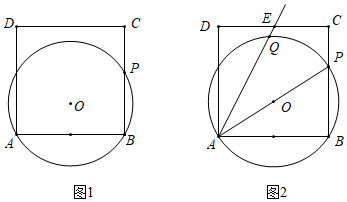 (1)、若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由;(2)、如图2,E是CD的中点,⊙O交射线AE于点Q,当AP平分∠EAB时,求tan∠EAP的值.25. 超市购进某种苹果,如果进价增加2元/千克要用300元;如果进价减少2元/千克,同样数量的苹果只用200元.(1)、求苹果的进价.(2)、如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元/千克.写出购进苹果的支出y(元)与购进数量x(千克)之间的函数关系式.(3)、超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完.据统计,销售单价z(元/千克)与一天销售数量x(千克)的关系为 .在(2)的条件下,要使超市销售苹果利润w(元)最大,求一天购进苹果数量.(利润=销售收入 购进支出)26. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF.
(1)、若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由;(2)、如图2,E是CD的中点,⊙O交射线AE于点Q,当AP平分∠EAB时,求tan∠EAP的值.25. 超市购进某种苹果,如果进价增加2元/千克要用300元;如果进价减少2元/千克,同样数量的苹果只用200元.(1)、求苹果的进价.(2)、如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元/千克.写出购进苹果的支出y(元)与购进数量x(千克)之间的函数关系式.(3)、超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完.据统计,销售单价z(元/千克)与一天销售数量x(千克)的关系为 .在(2)的条件下,要使超市销售苹果利润w(元)最大,求一天购进苹果数量.(利润=销售收入 购进支出)26. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF. (1)、求证:;(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.
(1)、求证:;(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.