内蒙古鄂尔多斯市2022年中考二模数学试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数-1， $- \sqrt{2}$ ，0， $\frac{1}{4}$ 中，最小的实数是（）．

A、-1 B、 $\frac{1}{4}$ C、0 D、 $- \sqrt{2}$

查看试题解析
2. 如图，该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 2021年国庆档电影《长津湖》仅10月1日当天的票房就达到了3.88亿元，创下了国庆档电影单日票房的记录．其中3.88亿元用科学记数法可表示为（）

A、 $3.88 \times 1 0^{7}$ 元 B、 $3.88 \times 1 0^{9}$ 元 C、 $0.388 \times 1 0^{10}$ 元 D、 $3.88 \times 1 0^{8}$ 元

查看试题解析
4. 为了增强学生预防新冠肺炎的安全意识，某校开展疫情防控知识竞赛．来自不同年级的30名参赛同学的得分情况如下表所示，这些成绩的中位数和众数分别是（）

成绩/分

84

88

92

96

100

人数/人

2

4

9

10

5

A、92分，96分 B、94分，96分 C、96分，96分 D、96分，100分

查看试题解析
5. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $2 a^{3} b \div b = 2 a^{3}$ C、 ${(2 a^{2})}^{4} = 8 a^{8}$ D、 ${(- a - b)}^{2} = a^{2} - b^{2}$

查看试题解析
6. 一副三角板如图所示摆放，若 $∠ 1 = 80 °$ ，则 $∠ 2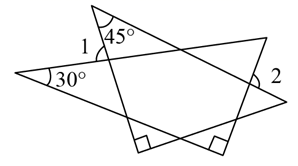$ 的度数是（）

A、80° B、95° C、100° D、110°

查看试题解析
7. 对于实数a、b，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如： $1 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x \otimes (- 2) = \frac{2}{x - 4} - 1$ 的解是（）

A、 $x = 5$ B、 $x = 6$ C、 $x = 7$ D、 $x = 8$

查看试题解析
8. 如图，边长为2的正方形 $A B C D$ 的对角线 $A C$ 与 $B D$ 交于点 $O$ ，将正方形 $A B C D$ 沿直线 $D F$ 折叠，点 $C$ 落在对角线 $B D$ 上的点 $E$ 处，折痕 $D F$ 交 $A C$ 于点 $M$ ，则 $O M$ 长是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{3} - 1$ D、 $2 - \sqrt{2}$

查看试题解析
9. 下列说法正确的个数是（）
①对角线相等的四边形是矩形②在函数 $y = \frac{\sqrt{x + 1}}{2 x - 3}$ 中，自变量x的取值范围是 $x \geq - 1$ ③菱形既是中心对称图形又是轴对称图形④若平均数相同的甲、乙两组数据， ${S_{甲}}^{2} = 0.3$ ， ${S_{乙}}^{2} = 0.02$ ，则乙组数据更稳定⑤ $\sqrt{16}$ 的算术平方根是4

A、1个 B、2个 C、3个 D、4个

查看试题解析
10.
如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，当P运动到B点时，P、Q两点同时停止运动．设P点运动的时间为t，△APQ的面积为S，则S与t的函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 不等式组 ${\begin{matrix} 3 x - 5 \geq 0 \\ x - 2 < 1 \end{matrix}$ 的整数解为．

查看试题解析
12. 如图，△ABC中，∠B=75°，∠C=30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，连结AD，则∠BAD的度数为．

查看试题解析
13. 如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是．

查看试题解析
14. 若等腰三角形的一边长是4，另两边的长是关于 $x$ 的方程 $x^{2} - 6 x + n = 0$ 的两个根，则 $n$ 的值为．

查看试题解析
15. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{2} x + 3$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 和点 $B$ ，点 $C$ 是线段 $A B$ 上一点，过点 $C$ 作 $C D ⊥ x$ 轴，垂足为 $D$ ， $C E ⊥ y$ 轴，垂足为 $E$ ， $S_{△ B E C} ： S_{△ C D A} = 4 ： 1$ ．若双曲线 $y = \frac{k}{x} (x > 0)$ 经过点 $C$ ，则 $k$ 的值为．

查看试题解析
16. 如图，下列各正方形中的四个数之间具有相同的规律．根据此规律，则第 $n$ 个图中的 $c =$ ．

查看试题解析

三、解答题

17.

(1)、计算： $2 s i n 60 ° + | \sqrt{3} - 2 | - {(\frac{1}{2})}^{- 1} + \frac{\sqrt{6} - \sqrt{2}}{\sqrt{2}}$

(2)、先化简，再求值： $1 - \frac{y - x}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}}$ ，其中 $x = 3$ ， $y = - 2$ ．

查看试题解析

18. 为庆祝中国共产党建党100周年，某校举行了“传党情，颂党恩”知识竞赛.为了解全校学生知识掌握情况，学校随机抽取部分竞赛成绩制定了不完整的统计表和频数分布直方图.

分数x（分）	频数（人）	频率
90≤x＜100	80	a
80≤x＜90	60	0.3
70≤x＜80		0.18
60≤x＜70	b	0.12

(1)、请直接写出表中a，b的值，并补全频数分布直方图；

(2)、竞赛成绩在80分以上（含80分）记为优秀，请估计该校3500名参赛学生中有多少名学生成绩优秀；

(3)、为了参加市上的“传党情，颂党恩”演讲比赛，学校从本次知识竞赛成绩优秀的学生中再次选拔出演讲水平较好的三位同学，其中男生一位、女生两位，现从中任选两位同学参加，请利用画树状图或列表的方法，求选中的两位同学恰好是一男一女的概率.

查看试题解析

19. 如图，张明站在河岸上的 $G$ 点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，他测得小船 $C$ 的俯角是 $∠ F D C = 30 °$ ，若张明的眼睛与地面的距离是1.5米， $B G = 1$ 米， $B G$ 平行于 $A C$ 所在的直线，迎水坡的坡度 $i = 4 ： 3$ ，坡长 $A B = 10$ 米，求小船C到岸边的距离 $C A$ 的长？（参考数据： $\sqrt{3} \approx 1.73$ ，结果精确到 $0.1$ ）

查看试题解析
20. 疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $a$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $y$ （万人）与各自接种时间 $x$ （天）之间的关系如图所示．

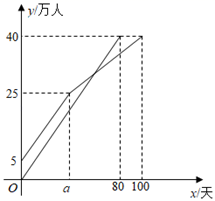(1)、直接写出乙地每天接种的人数及 $a$ 的值；

(2)、当甲地接种速度放缓后，求 $y$ 关于 $x$ 的函数解析式，并写出自变量 $x$ 的取值范围；

(3)、当乙地完成接种任务时，求甲地未接种疫苗的人数．

查看试题解析
21. 如图，在⊙O中，AB是直径，弦CD⊥AB，垂足为H，E为 $\overset{⌢}{B C}$ 上一点，F为弦DC延长线上一点，连接FE并延长交直径AB的延长线于点G，连接AE交CD于点P，若FE＝FP．

(1)、求证：FE是⊙O的切线；

(2)、若⊙O的半径为8，sinF＝ $\frac{3}{5}$ ，求BG的长．

查看试题解析
22. 一商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元/件）（x为正整数）之间满足一次函数关系y=−50x+1200．

(1)、求一周内该商场销售这种商品获得的最大利润及此时的售价分别为多少元？

(2)、若某一周该商品的销售量不少于600件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？

查看试题解析
23. 在△ABC中，∠C＝90°，AC＝BC＝2，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于点D、点E，图①，②，③是旋转得到的三种图形．

(1)、观察线段PD和PE之间有怎样的大小关系？并以图②为例，并加以证明；

(2)、观察线段CD、CE和BC之间有怎样的数量关系？并以图③为例，并加以证明；

(3)、△PBE是否能成为等腰三角形？若能，求出∠PEB的度数；若不能，请说明理由．

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x - 3$ 与x轴交于 $A (- 2 ， 0)$ ， $B (6 ， 0)$ 两点，与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为 $(4 ， - 3)$ ．

(1)、求抛物线的解析式；

(2)、若点P是抛物线上的点，点P的横坐标为 $m (m \geq 0)$ ，过点P作 $P M ⊥ x$ 轴，垂足为M．PM与直线l交于点N，当点N是线段PM的三等分点时，求点P的坐标；

(3)、若点Q是y轴上的点，且 $∠ A D Q = 45 °$ ，求点Q的坐标．

查看试题解析

成绩/分	84	88	92	96	100
人数/人	2	4	9	10	5