内蒙古赤峰市敖汉旗2022年中考模拟考试数学试卷（一）

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果规定收入为正，那么支出为负，收入2元记作＋2，那么支出3元记作（）

A、－3 B、－1 C、1 D、3

查看试题解析
2. 2020年6月23日9时43分，我国成功发射了北斗系统第55颗导航卫星，其授时精度为世界之最，不超过0.000 000 009 9秒.数据“0. 000 000 009 9”用科学记数法表示为（）

A、 $99 \times 10^{- 10}$ B、 $9.9 \times 10^{- 10}$ C、 $9.9 \times 10^{- 9}$ D、 $9.9 \times 10^{- 8}$

查看试题解析
3. 一个两位数，它的十位数字是a，个位数字是b，这个两位数是（）

A、 $a + b$ B、 $a b$ C、 $10 a b$ D、 $10 a + b$

查看试题解析
4. 下列既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是（）

A、a²+a³=a⁵ B、 $3 \sqrt{2} - \sqrt{2} = 1$ C、（x²）³=x⁵ D、m⁵÷m³=m²

查看试题解析
6. 数轴上表示数 $m$ 和 $m + 2$ 的点到原点的距离相等，则 $m$ 为（）

A、-2 B、2 C、1 D、-1

查看试题解析
7. 将一个长方形纸片按如图所示的方式折叠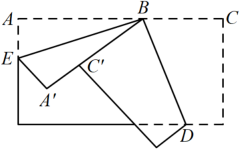， $B D$ 、 $B E$ 为折痕，若 $∠ A B E = 20 °$ ，则 $∠ C B D$ 等于（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
8. 已知x，y满足方程组 ${\begin{array}{l} 2 x + 3 y = 35 \\ 3 x + 2 y = 40 \end{array}$ ，则 $x + y$ 的值为（）

A、15 B、18 C、20 D、22

查看试题解析
9. 一个几何体的三视图如图所示，这个几何体的侧面积为（）

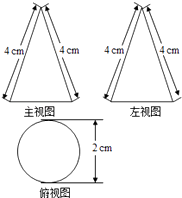A、2πcm² B、4πcm² C、8πcm² D、16πcm²

查看试题解析

10. 为迎接中国共产党建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖．

成绩/分	91	92	93	94	95	96	97	98	99	100
人数	■	■	1	2	3	5	6	8	10	12

下列关于成绩的统计量中，与被遮盖的数据无关的是（）

A、平均数，方差 B、中位数，方差 C、中位数，众数 D、平均数，众数

查看试题解析

11. 如果不等式组 ${\begin{array}{l} x + 5 < 4 x - 1 \\ x > m \end{array}$ 的解集为 $x > 2$ ，那么 $m$ 的取值范围是（）

A、 $m \leq 2$ B、 $m \geq 2$ C、 $m > 2$ D、 $m < 2$

查看试题解析
12. 如图，在 $△ A B C$ 中， $C D$ 平分 $∠ A C B$ ，交 $A B$ 于点D， $B E$ 平分 $∠ A B C$ ，交 $C D$ 于点E， $A E$ 的延长线交 $B C$ 于点F，若 $A B = A C = 5$ ， $B C = 6$ ， $△ B E F$ 与 $△ A B E$ 的面积比为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
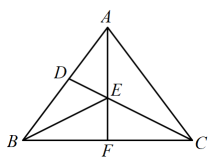13. 如图，点B在反比例函数 $y = \frac{6}{x}$ （ $x > 0$ ）的图象上，点C在反比例函数 $y = - \frac{2}{x}$ （ $x > 0$ ）的图象上，且 $B C / / y$ 轴， $A C ⊥ B C$ ，垂足为点C ，交y轴于点A ，则 $△ A B C$ 的面积为（）

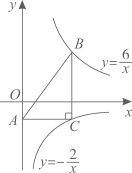A、3 B、4 C、5 D、6

查看试题解析
14. 如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2 $\sqrt{3}$ ，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM＝x，则S关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

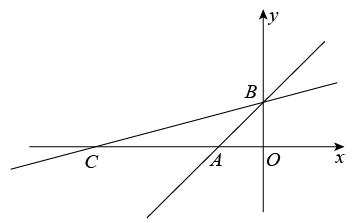
15. 如图一次函数 $y = x + \sqrt{3}$ 的图象与x轴、y轴分别交于点A、B，把直线 $A B$ 绕点B顺时针旋转 $30 °$ 交x轴于点C．则线段 $A C$ 的长为．

查看试题解析
16. 如图是一架人字梯，已知 $A B = A C = 2$ 米， $A C$ 与地面 $B C$ 的夹角为 $β$ ，则两梯脚之间的距离 $B C$ 为米．

查看试题解析
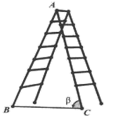17. 在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点A的概率是．

查看试题解析
18. 如图，在矩形 $A B C D$ 中， $A B = 4 c m$ ， $A D = 12 c m$ ， P点在 $A D$ 边上以每秒 $1 c m$ 的速度从A向D运动，点Q在 $B C$ 边上，以每秒 $4 c m$ 的速度从C点出发，在C、B间往返运动，两点同时出发，P点到达D点时同时停止，在这段时间内，有如下说法：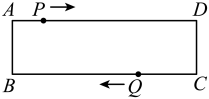
①该过程中，会出现4次 $P Q ∥ A B$ 的时刻；
②该过程中，会出现3次四边形 $A B Q P$ 和四边形 $P Q C D$ 同时为矩形的时刻；
③该过程中，当： $t = 5$ 时，四边形 $A B Q P$ 和四边形 $P Q C D$ 的面积比为6∶5；
④该过程中，矩形 $A B Q P$ 和 $P Q C D$ 面积比的最大值为4∶3．
上述说法正确的是（填序号）．

查看试题解析

三、解答题

19. 先化简在求值： $\frac{2 x - 6}{x - 2} \div (\frac{5}{x - 2} - x - 2)$ ，在 $0 < x < 4$ 的整数中选择合适的数代入求值.

查看试题解析
20. 如图 $R t △ A B C$ 中， $∠ A C B = 90 °$

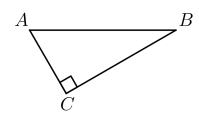(1)、利用尺规作图，作 $⊙ C$ ，使它与 $A B$ 相切于点D、与 $A C$ 相交于点E（保留作痕迹，不写作法）．

(2)、在（1）的基础上，若 $B C = 3$ ， $∠ A = 60 °$ ，求弧 $D E$ 的长．

查看试题解析
21. 2021年，黄冈、咸宁、孝感三市实行中考联合命题，为确保联合命题的公平性，决定采取三轮抽签的方式来确定各市选派命题组长的学科.第一轮，各市从语文、数学、英语三个学科中随机抽取一科；第二轮，各市从物理、化学、历史三个学科中随机抽取一科；第三轮，各市从道德与法治、地理、生物三个学科中随机抽取一科.

(1)、黄冈在第一轮抽到语文学科的概率是；

(2)、用画树状图或列表法求黄冈在第二轮和第三轮抽签中，抽到的学科恰好是历史和地理的概率.

查看试题解析
22. 中国发展到今天，交通已经成为影响社会发展快慢的重要因素，以我旗为例：从贝子府镇到新惠镇全程50千米，为普通国路标准路面；从四家子镇到新惠镇全程60千米，为一级路标准路面．汽车在一级路上行驶的平均速度是在普通国路上的 $\frac{5}{3}$ 倍，用时少14分钟．求汽车从贝子府镇到新惠镇需要多长时间．

查看试题解析
23. 如图，AB是⊙O的直径，点C、D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F，G为AB的下半圆弧的中点，DG交AB于H，连接DB、GB．

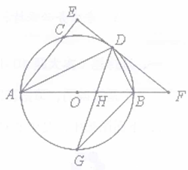(1)、证明EF是⊙O的切线；

(2)、求证：∠DGB=∠BDF：

(3)、已知圆的半径R=5，BH=3，求GH的长．

查看试题解析
24. 阅读下列材料，按要求解答问题：
阅读理解：若p、q、m为整数，且三次方程 $x^{3} + p x^{2} + q x + m = 0$ 有整数解c，则将c代入方程得： $c^{3} + p c^{2} + q c + m = 0$ ，移项得： $m = - c^{3} - p c^{2} - q c$ ，即有： $m = c \times (- c^{2} - p c - q)$ ，由于 $- c^{2} - p c - q$ 与c及m都是整数，所以c是m的因数．
上述过程说明：整数系数方程 $x^{3} + p x^{2} + q x + m = 0$ 的整数解只可能是m的因数．
例如：方程 $x^{3} + 4 x^{2} + 3 x - 2 = 0$ 中－2的因数为±1和±2，将它们分别代入方程 $x^{3} + 4 x^{2} + 3 x - 2 = 0$ 进行验证得：x=－2是该方程的整数解，－1、1、2不是方程的整数解．
解决问题：
①根据上面的学习，请你确定方程 $x^{3} + x^{2} + 5 x + 7 = 0$ 的整数解只可能是哪几个整数？
②方程 $x^{3} - 2 x^{2} - 4 x + 3 = 0$ 是否有整数解？若有，请求出其整数解；若没有，请说明理由.

查看试题解析
25. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + 2 a x + c$ （其中a、c为常数，且 $a < 0$ ）与x轴的一个交点为 $A (- 3 ， 0)$ ，与y轴交于点B，此抛物线顶点C的纵坐标为4．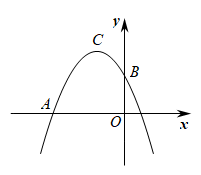

(1)、求抛物线的解析式；

(2)、求 $∠ C A B$ 的正切值；

查看试题解析
26. 如图

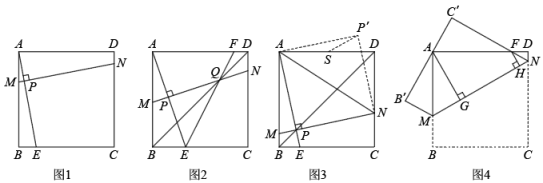(1)、问题情境：
如图1，在正方形 $A B C D$ 中， $E$ 为边 $B C$ 上一点 $($ 不与点 $B$ 、 $C$ 重合 $)$ ，垂直于 $A E$ 的一条直线 $M N$ 分别交 $A B$ 、 $A E$ 、 $C D$ 于点 $M$ 、 $P$ 、 $N$ ．则 $D N$ 、 $M B$ 、 $E C$ 之间的数量关系为_ ．

(2)、问题探究：在“问题情境”的基础上．
如图2，若垂足 $P$ 恰好为 $A E$ 的中点，连接 $B D$ ，交 $M N$ 于点 $Q$ ，连接 $E Q$ ，并延长交边 $A D$ 于点 $F .$ 求 $∠ A E F$ 的度数；

(3)、如图3，当垂足 $P$ 在正方形 $A B C D$ 的对角线 $B D$ 上时，连接 $A N$ ，将 $△ A P N$ 沿着 $A N$ 翻折，点 $P$ 落在点 $P^{'}$ 处，若正方形 $A B C D$ 的边长为4， $A D$ 的中点为 $S$ ，求 $P^{^{'}} S$ 的最小值．

(4)、如图4，在边长为 $4$ 的正方形 $A B C D$ 中，点 $M$ 、 $N$ 分别为边 $A B$ 、 $C D$ 上的点，将正方形 $A B C D$ 沿着 $M N$ 翻折，使得 $B C$ 的对应边 $B^{^{'}} C^{^{'}}$ 恰好经过点 $A$ ， $C^{'} N$ 交 $A D$ 于点 $F .$ 分别过点 $A$ 、 $F$ 作 $A G ⊥ M N$ ， $F H ⊥ M N$ ，垂足分别为 $G$ 、 $H$ ，若 $A G = \frac{5}{2}$ ，请直接写出 $F H$ 的长．

查看试题解析