江西省南昌市2022年九年级初中学业水第二次调研数学试题

试卷更新日期：2023-03-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 1)^{2}$ 的结果是（）

A、1 B、-1 C、2 D、-2

查看试题解析
2. 截至2021年12月31日，我国碳排放配额累计成交量1.79亿吨，累计成交额76.61亿元为我国低碳转型注入活力．将1.79亿用科学记数法表示为（）

A、 $1.79 \times 1 0^{7}$ B、 $17.9 \times 1 0^{7}$ C、 $1.79 \times 1 0^{8}$ D、 $17.9 \times 1 0^{8}$

查看试题解析
3. 没有哪一门学科能像数学这样，利用如此多的符号图形，展现一系列完备且完美的世界．下面是由4个数学式子绘制成的完美曲线，其中不是轴对称图形的是（）

A、笛卡尔心形线 B、三叶玫瑰形曲线 C、蝴蝶形曲线 D、太极曲线

查看试题解析
4. 如图，AB与CD相交于点O，OE是 $∠ A O C$ 的平分线，且OC恰好平分 $∠ E O B$ ，则下列结论中：① $∠ A O E = ∠ E O C$ ；② $∠ E O C = ∠ C O B$ ；③ $∠ A O D = ∠ A O E$ ；④ $∠ D O B = 2 ∠ A O D$ ，正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 已知抛物线 $y = - (x - m)^{2} + 2 m$ 过不同的两点 $A (a ， n)$ ， $B (b ， n)$ ，则当点 $C (a + b ， m)$ 在该函数图象上时，m的值为（）

A、0 B、1 C、0或1 D、±1

查看试题解析
6. 如图，是由4个完全相同的小正方体组成的几何体，移动1，2，3三个小正方体中的一个，使移动前后的几何体的左视图不变，要求这个被移动的小正方体与剩下的未移动的小正方体至少共一个面，则移动的方法有（）种

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

7. 计算： $\sqrt{8}$ =

查看试题解析
8. 若一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两个实数根为 $a$ ， $b$ ，则 $a - a b + b$ 的值为．

查看试题解析
9. 北京2022年冬奥会开启“坐着高铁看冬奥”新模式．北京赛区到延庆赛区乘高铁与乘班车通行路程均约60公里，已知高铁的平均速度是班车平均速度的3倍，乘高铁用时比乘班车少40分钟，则从北京赛区到延庆赛区乘高铁所需时间约为分钟．

查看试题解析
10. 如图，点E是矩形ABCD边AB上一点，将 $△ A D E$ 沿着DE翻折得到 $△ A^{'} D E$ ， $A^{'} E$ 与DC交于F点，若 $A D = \sqrt{3}$ ， $A E = 3$ ，则 $E F =$ ．

查看试题解析
11. 为加强五项管理，某校就“作业管理”“睡眠管理”“手机管理”“读物管理”“体质管理”五个方面对各班进行考核打分（各项满分均为100），各项在考核中所占比例和该校七（1）班在五个方面得分如下表：
项目
作业管理
睡眠管理
手机管理
读物管理
体质管理
所占比例
30%
10%
25%
10%
25%
七（1）班得分
85
78
98
100
86
则该班在本校五项管理考核中，综合得分 $=$ ．

查看试题解析
12. 如图，AB和OC分别是 $⊙ O$ 的直径和半径， $∠ B O C = 60 °$ ，点P是直径AB上的一个动点，射线CP与 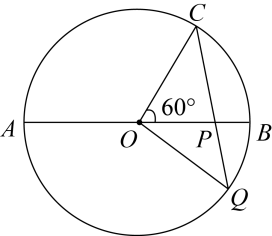$⊙ O$ 相交于点Q，若 $△ P O Q$ 是等腰三角形，则 $∠ C P B =$ ．

查看试题解析

三、解答题

13.

(1)、计算： $\frac{1}{2} + s i n 30 ° - | - 1 |$ ；

(2)、化简： $\frac{1}{x^{2} - 1} \div \frac{1}{x^{2} - x}$ ．

查看试题解析
14. 如图，在正方形ABCD中， $A B = 4 c m$ ，延长AB至点E，使 $B E = 8 c m$ ， F是DE的中点，求线段BF的长度．

查看试题解析
15. 如图，在平面直角坐标系中，折线 $O - A - B$ 是某函数的图象，A，B的坐标分别为 $(2 ， 6)$ 和 $(6 ， 9)$ ，请仅用无刻度的直尺，分别在图1，图2中按下列要求画图．

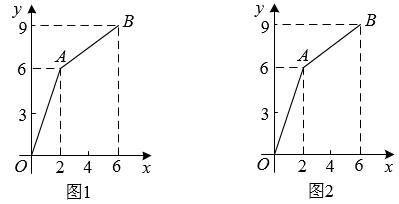(1)、在图1中，画平行四边形AOCB；

(2)、在图2中，画与OA平行且平分平行四边形AOCB面积的直线l．

查看试题解析
16. 小明、小张春季开学约伴从A地到C地上大学，需途径B地中转，从A地去B地有3种途径，从B地去C地有2种途径，两人意见不一致，于是通过翻牌游戏来决定行程，游戏过程如下：第一步：先在五张反面完全一样的扑克牌的正面分别写上 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， $C_{1}$ ， $C_{2}$ ，约定， $B_{1}$ ， $B_{2}$ ， $B_{3}$ 分别代表A地到B地的3种途径， $C_{1}$ ， $C_{2}$ 分别代表B地去C地的2种途径；第二步：先把 $B_{1}$ ， $B_{2}$ ， $B_{3}$ 三张牌反扣桌面，随机抽取一张；第三步：再把 $C_{1}$ ， $C_{2}$ 两张牌反扣桌面，随机再抽取一张．

(1)、“抽到路径 $B_{1}$ ”是事件（填“必然”或“不可能”或“随机”）；

(2)、用树状图或列表法，求事件“从A到C的路径，恰好抽到 $A - B_{1} - C_{1}$ 这条路径”的概率．

查看试题解析
17. 为奖励成绩进步突出的学生，某班班委计划购买A，B，C三种奖品，已知买2个A种奖品和4个B种奖品共花100元；买3个A种奖品和2个B种奖品共花70元．

(1)、求A，B两种奖品的单价；

(2)、该班班委现有班费190元，他们想三种奖品均购买，且购买B种奖品不少于3个，C种奖品不超过2个，已知C种奖品每个30元，若要实现该班班委的全部想法，问他们最多能购买多少件A种奖品？

查看试题解析
18. 根据教育部对中学生家庭作业时间管理的要求，规定中学生每天家庭作业时间不超过1.5小时（90分钟）．为符合作业管理要求．某校对该校七年级学生一周的“家庭作业时间”（单位：小时）进行了随机抽样调查，根据作业时间分成了A，B，C，D，E五类，并将获得的数据绘制成如下统计图表，请根据图表中的信息回答下列问题．
项目（周家庭作业时间：小时）
频数
频率
$A ： (0 \leq t < 3.5)$
2
0.04
$B ： (3.5 \leq t < 7)$
10
0.20
$C ： (7 \leq t < 10.5)$
18
n
$D ： (10.5 \leq t < 14)$
m
0.28
$E ： (14 \leq t < 17.5)$
6
0.12

(1)、求统计表中m，n的值；

(2)、补全条形统计图；

(3)、甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”，求甲同学的周学习时间在哪个范围内；

(4)、已知该校七年级学生约有800人，试估计该校七年级学生每周“家庭作业时间”符合作业管理要求的人数．

查看试题解析
19. 如图，在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象同时经过点 $A (2 ， m)$ ， $B (4 ， n)$ 两点．

(1)、则 $\frac{n}{m} =$ ．

(2)、若 $∠ O A B = 90 °$ ．
①求反比例函数的解析式；
②延长AB交x轴于C点，求C点坐标．

查看试题解析
20. 如图1，是某品牌的可伸缩篮球架，其侧面可抽象成图2，结点F，G，H，M，N可随着伸缩杆EF的伸缩转动，从而控制篮球圈ON离地面AB的高度， $O N ∥ A B$ ，主杆 $A H ⊥ A B$ ， G，C，D均在主于AH上，结点N，G，F共线， $D E ∥ A B$ ，经测量， $A D = 150 c m$ ， $D C = C G = G H = M N = G F = 50 c m$ ， $M H = N G = G D$ ， $∠ N G D = 33 °$ ，此时， $E F ∥ A H$ ．（结果保留小数点后一位）

(1)、① $∠ M =$ ▲ °，EF与AB的位置关系 ▲ ；
②求EF的长度．

(2)、在图1的基础上，调节伸缩杆EF，得到图3，图4是图3的示意图，经测量，此时，篮球圈ON离地面AB的高度刚好达到国际标准 $305 c m$ ，求NF绕着G点顺时针旋转的度数．（参考数据： $s i n 57 ° \approx 0.84$ ， $c o s 57 ° \approx 0.55$ ， $t a n 57 ° \approx 1.54$ ）

查看试题解析
21. 如图，点B为半 $⊙ O$ 外一点，AC为直径， $B C ⊥ A C$ ， $A C = 8$ ， $B C = 6$ ， AB与半 $⊙ O$ 交于点E，点P是AE上一动点，过点P作 $P D ⊥ A B$ 交 $\overset{⌢}{A E}$ 于点D．

(1)、DP的最大值 $=$ ；

(2)、如图1，当 $t a n ∠ D B O = \frac{2}{3}$ 时，求证：BD是 $⊙ O$ 的切线；

(3)、如图2，当点D在 $\overset{⌢}{A C}$ 的中点时，求图中阴影部分的周长．

查看试题解析
22. 已知二次函数 $C_{1} ： y = x^{2} - 2 m x + 2 m^{2} - 2 m - 3$ （m为常数）．

(1)、二次函数 $C_{1}$ 的顶点坐标P（，）（用含m的代数式表示）；

(2)、m取不同的值，可以得到不同的点P，分别用 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ ， $P_{5}$ 表示．

…
$P_{1}$
$P_{2}$
$P_{3}$
$P_{4}$
$P_{5}$
…
P点横坐标
…
-1
0
1
2
3
…
P点纵坐标
…
0
-3
-4
a
0
…
①补全表格；
②在图1中描出m取不同值时得到的 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ ， $P_{5}$ 各点，再用平滑的曲线依次连接各点，得到的图象记为 $C_{2}$ ．并求曲线 $C_{2}$ 的解析式．

(3)、若 $C_{1}$ 和x轴有两个交点，当这两个点与二次函数 $C_{1}$ 的顶点P构成等腰直角三角形时，求m的值．

查看试题解析
23. 如图1，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = B C$ ， AO是BC边上的中线，点D是AO上一点， $D E ⊥ E O$ ， E是垂足， $△ D E O$ 可绕着点O旋转，点F是点E关于点O的对称点，连接AD和CF．

(1)、问题发现：如图2，当 $\frac{A D}{D O} = 1$ 时，则下列结论正确的是．（填序号）
① $B E = C F$ ；②点F是OC的中点：③AO是 $∠ B A C$ 的角平分线；④ $A D = \sqrt{5} C F$ ．

(2)、数学思考：将图2中 $△ D E O$ 绕点O旋转，如图3，则AD和CF具有怎样的数量关系？请给出证明过程；

(3)、拓展应用：在图1中，若 $\frac{A D}{D O} = x$ ，将 $△ D E O$ 绕着点O旋转．
①则 $A D =$ ▲ CF；
②若 $A B = 4$ ， $x = 1$ ，在 $△ D E O$ 旋转过程中，如图4，当点D落在AB上时，连结BE，EC，求四边形ABEC的面积．

查看试题解析

项目	作业管理	睡眠管理	手机管理	读物管理	体质管理
所占比例	30%	10%	25%	10%	25%
七（1）班得分	85	78	98	100	86

项目（周家庭作业时间：小时）	频数	频率
$A ： (0 \leq t < 3.5)$	2	0.04
$B ： (3.5 \leq t < 7)$	10	0.20
$C ： (7 \leq t < 10.5)$	18	n
$D ： (10.5 \leq t < 14)$	m	0.28
$E ： (14 \leq t < 17.5)$	6	0.12

	…	$P_{1}$	$P_{2}$	$P_{3}$	$P_{4}$	$P_{5}$	…
P点横坐标	…	-1	0	1	2	3	…
P点纵坐标	…	0	-3	-4	a	0	…