江西省九江市2022年初中学业水平模拟数学一模试题
试卷更新日期:2023-03-17 类型:中考模拟
一、单选题
-
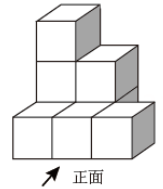
1. ﹣5的绝对值是( )A、5 B、﹣5 C、 D、2. 北京2022年冬奥会向全球招募27000名志愿者,其中数27000用科学记数法表示为( )A、 B、 C、 D、3. 如图是由8个相同的小正方体组成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、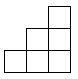 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )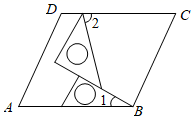 A、 B、 C、 D、6. 如图,在已知线段AB上按下列步骤作图:(1)分别以点A,B为圆心,以大于长为半径作弧交于C、D两点,直线CD与AB交于点E;(2)以点E为圆心,以AE长为半径作弧交AC于点F,连接EF和FB;若 , 则( )
A、 B、 C、 D、6. 如图,在已知线段AB上按下列步骤作图:(1)分别以点A,B为圆心,以大于长为半径作弧交于C、D两点,直线CD与AB交于点E;(2)以点E为圆心,以AE长为半径作弧交AC于点F,连接EF和FB;若 , 则( ) A、5° B、10° C、12° D、15°
A、5° B、10° C、12° D、15°二、填空题
-
7. 计算:-3+2= .8. 因式分解= .9. 已知 , 是一元二次方程的两根,若 , 则 .10. 小雪在练习仰卧起坐时,前4组的成绩(个/分)分别为:42、48、52、48.若要使5组成绩的平均数与众数相同.则小雪第5组成绩是个/分.11. 如图,在矩形ABCD中, , , 点E在边上运动,设线段CE的长度为m,则m的取值范围是 .
 12. 如图,在中, , AD是BC边上的高,图中线段上一动点E,若满足 , , , 则以AE为边长的正方形面积是 .
12. 如图,在中, , AD是BC边上的高,图中线段上一动点E,若满足 , , , 则以AE为边长的正方形面积是 .
三、解答题
-
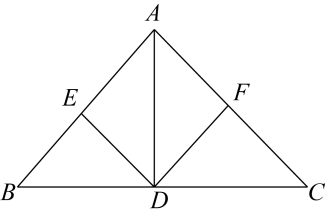
13.(1)、计算:;(2)、如图,在中,点D是BC边中点, , 点E和F分别是AB、AC边的中点,求证:
 14. 先化简,再求值: ,其中 .15. 下面四张卡片上分别给有2022年北京冬奥会会徽、志愿者徽标、吉祥物冰墩墩和雪容融图案,它们形状大小背面完全一样,现把四张卡片背面朝上打乱放在桌面上.
14. 先化简,再求值: ,其中 .15. 下面四张卡片上分别给有2022年北京冬奥会会徽、志愿者徽标、吉祥物冰墩墩和雪容融图案,它们形状大小背面完全一样,现把四张卡片背面朝上打乱放在桌面上. (1)、小志同学从中抽取一张是会徽卡片的是将事件(填“随机”或“不可能”或“必然”);(2)、小志同学从中抽取两张卡片,正好是两张吉祥物图案,请你用列表法或画树状图法表示出这次抽取所有可能的结果,并求出它的概率.16. 请仅用无刻度的直尺,分别按下列要求画图(保留画图痕迹).
(1)、小志同学从中抽取一张是会徽卡片的是将事件(填“随机”或“不可能”或“必然”);(2)、小志同学从中抽取两张卡片,正好是两张吉祥物图案,请你用列表法或画树状图法表示出这次抽取所有可能的结果,并求出它的概率.16. 请仅用无刻度的直尺,分别按下列要求画图(保留画图痕迹).
 (1)、在图①中,已知平行四边形ABCD边AB的中点E,画出CD边上的中点;(2)、在图②中,已知四边形ABCE中, , , 点F是边BC中点,画出以AB、BC为边的平行四边形ABCD.17. 如图,AB和与x轴垂直,A点坐标是 , 和是位似三角形,且位似比是 , 点C是的中点,反比例函数的图象经过点C,与交于点D.
(1)、在图①中,已知平行四边形ABCD边AB的中点E,画出CD边上的中点;(2)、在图②中,已知四边形ABCE中, , , 点F是边BC中点,画出以AB、BC为边的平行四边形ABCD.17. 如图,AB和与x轴垂直,A点坐标是 , 和是位似三角形,且位似比是 , 点C是的中点,反比例函数的图象经过点C,与交于点D. (1)、求点D坐标;(2)、连接BD、CD,求四边形ABDC的面积.18. 某汽车贸易公司销售A、B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用不超过300万元资金,采购A、B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?19. 为庆祝中国共产党建党100周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 五个等级,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
(1)、求点D坐标;(2)、连接BD、CD,求四边形ABDC的面积.18. 某汽车贸易公司销售A、B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用不超过300万元资金,采购A、B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?19. 为庆祝中国共产党建党100周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 五个等级,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:等级
成绩
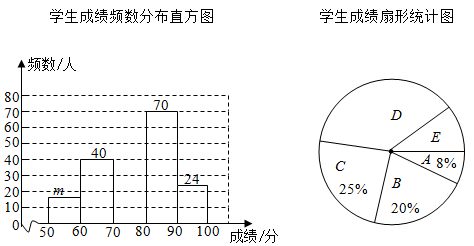 (1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 ;(2)、补全学生成绩频数分布直方图;(3)、所抽取学生成绩的中位数落在等级;(4)、若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少人?20. 如图①是大家熟悉的柜式空调,关闭时叶片竖直向下.如图②,当启动时,出风口叶片会同步开始逆时针旋转到最大旋转角90°时返回,旋转速度是每秒10°,同时空调风从叶片口直线吹出.AB由5个叶片组成的出风口,经过测量,A点、B点距地面高度分别是170cm、145cm在空调正前方100cm处站着一个高70cm的小朋友(线段EF表示).
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 ;(2)、补全学生成绩频数分布直方图;(3)、所抽取学生成绩的中位数落在等级;(4)、若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少人?20. 如图①是大家熟悉的柜式空调,关闭时叶片竖直向下.如图②,当启动时,出风口叶片会同步开始逆时针旋转到最大旋转角90°时返回,旋转速度是每秒10°,同时空调风从叶片口直线吹出.AB由5个叶片组成的出风口,经过测量,A点、B点距地面高度分别是170cm、145cm在空调正前方100cm处站着一个高70cm的小朋友(线段EF表示). (1)、从启动开始,多长时间小朋友头顶E处感受到空调风;(2)、若叶片从闭合旋转到最大角度的过程中,小朋友的头顶E处有多长时间感受到空调风;(3)、当选择上下扫风模式时,叶片会旋转到最大角度后原速返回.从启动到第一次返回起始位的过程中,该小朋友头顶E处从第一次感受到空调风到再次感受到空调风中间间隔了多长时间.(参考数据: , , )21. 如图,A、B、C、D是上的四个点, , 点E是弦BC延长线上一点,连接DE,满足 .
(1)、从启动开始,多长时间小朋友头顶E处感受到空调风;(2)、若叶片从闭合旋转到最大角度的过程中,小朋友的头顶E处有多长时间感受到空调风;(3)、当选择上下扫风模式时,叶片会旋转到最大角度后原速返回.从启动到第一次返回起始位的过程中,该小朋友头顶E处从第一次感受到空调风到再次感受到空调风中间间隔了多长时间.(参考数据: , , )21. 如图,A、B、C、D是上的四个点, , 点E是弦BC延长线上一点,连接DE,满足 . (1)、如图①,求证:DE是的切线;(2)、如图②,若点是优弧中点,的半径长为3,求的值.22. 如图(1),在四边形ABCD中, , , 以点A为顶点作 , 且 , 连接EF.
(1)、如图①,求证:DE是的切线;(2)、如图②,若点是优弧中点,的半径长为3,求的值.22. 如图(1),在四边形ABCD中, , , 以点A为顶点作 , 且 , 连接EF. (1)、观察猜想 如图(2),当时,
(1)、观察猜想 如图(2),当时,①四边形ABCD是(填特殊四边形的名称);
②BE,DF,EF之间的数量关系为 .
(2)、类比探究 如图(1),线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请加以证明;若不成立,请说明理由.(3)、解决问题 如图(3),在中, , , 点D,E均在边BC上,且 , 若 , 求DE的长.23. 抛物线的一般表达式为(a、b、c为常数,),若抛物线经过原点,则把这种经过原点的抛物线称为“过零抛物线”,(1)、过零抛物线的顶点满足下列条件:①当顶点坐标为时,则 , ;
②当顶点坐标为 , 且时,则a与e之间的关系式是 .
(2)、当过零抛物线的顶点在直线上,且时,用含k的代数式表示b.(3)、现有一组过零抛物线,它们的顶点 , , …,在直线上,其横坐标依次为1,2,…,n(n为正整数,且),分别过每个顶点作x轴的垂线,垂足分别记为 , , …, , 以线段和为边向右作平行四边形 , 若这组抛物线中的某一条经过点 , 求此时满足条件的平行四边形的点坐标.